Sediment transport following water transfer from Yangtze River to Taihu Basin
Zheng GONG, Chang-kuan ZHANG*, Cheng-biao ZUO, Wei-deng WU
1. State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering, Hohai University, Nanjing 210098, P. R. China
2. Laboratory of Ocean Dynamics, Third Institute of Oceanography, State Oceanic Administration, Xiamen 361005, P. R. China
Sediment transport following water transfer from Yangtze River to Taihu Basin
Zheng GONG1, Chang-kuan ZHANG*1, Cheng-biao ZUO1, Wei-deng WU2
1. State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering, Hohai University, Nanjing 210098, P. R. China
2. Laboratory of Ocean Dynamics, Third Institute of Oceanography, State Oceanic Administration, Xiamen 361005, P. R. China
To meet the increasing need of fresh water and to improve the water quality of Taihu Lake, water transfer from the Yangtze River was initiated in 2002. This study was performed to investigate the sediment distribution along the river course following water transfer. A rainfall-runoff model was first built to calculate the runoff of the Taihu Basin in 2003. Then, the flow patterns of river networks were simulated using a one-dimensional river network hydrodynamic model. Based on the boundary conditions of the flow in tributaries of the Wangyu River and the water level in Taihu Lake, a one-dimensional hydrodynamic and sediment transport numerical model of the Wangyu River was built to analyze the influences of the inflow rate of the water transfer and the suspended sediment concentration (SSC) of inflow on the sediment transport. The results show that the water transfer inflow rate and SSC of inflow have significant effects on the sediment distribution. The higher the inflow rate or SSC of inflow is, the higher the SSC value is at certain cross-sections along the river course of water transfer. Higher inflow rate and SSC of inflow contribute to higher sediment deposition per kilometer and sediment thickness. It is also concluded that a sharp decrease of the inflow velocity at the entrance of the Wangyu River on the river course of water transfer induces intense sedimentation at the cross-section near the Changshu hydro-junction. With an increasing distance from the Changshu hydro-junction, the sediment deposition and sedimentation thickness decrease gradually along the river course.
Taihu Basin; Taihu Lake; river network; water transfer; rainfall-runoff model; 1-D hydrodynamic numerical model; cohesive sediment
1 Introduction
The Taihu Basin is situated in the southern wing of the Yangtze Estuary with an area of 36 895 km2, covering the south of Jiangsu Province, the north of Zhejiang Province, and the mainland of Shanghai City (Gong and Lin 2009). The basin area accounts for 0.4% of the Chinese territory land, and the corresponding GDP accounts for 11% of China. The basin shows the characteristics of high population density, urbanization, and economic development(Yang and Wang 2003). Taihu Lake, the third largest fresh water lake of China, lies in the center of the basin with an area of 2 338 km2and a mean depth of 1.9 m. Taihu Lake has multiple service functions, e.g., drinking water resources, irrigation, shipping, fishery, tourism, etc. (Qin et al. 2007; Hu et al. 2008) With the rapid social and economic development, industrial wastewater, agricultural activities, and urban runoff cause serious water pollution and, consequently, quality-related water scarcity (Hu et al. 2008; Zhu et al. 2008; Jiang 2009; Huang et al. 2010). In summer, autumn and even spring of recent years, the northern and western parts of Taihu Lake are often covered with algae (Hu et al. 2008). Harmful algae in Taihu Lake are worsening due to excessive pollutants discharged into the lake (Dong et al. 2008). Some measures have been employed to improve the water quality and restore the aquatic ecosystem, including standardized emission of pollutants, treatment of domestic wastewater, implementation of physico-ecological engineering, and sediment dredging (Pu et al. 1998; Wang et al. 2006; Li et al. 2010). Although these measures have some effects on water quality improvement, long-term effectiveness and potential impacts on the ecosystem of the Taihu Basin remain uncertain, and further investigations are required (Wang et al. 2006). Furthermore, it is also difficult to realize the overall standardized emission of pollutants and effective treatment of domestic wastewater (Schwartz 2003). For delta areas, water transfer from adjacent estuaries to supply fresh water is often a feasible measure to improve the water quality of these areas because of its low cost, easy conduction, and effective deduction of nutrients (Hu et al. 2010).
In the Taihu Basin, water transfer from the Yangtze River to Taihu Lake was initiated in 2002 in an attempt to dilute polluted water and flush pollutants out of Taihu Lake and river networks (Wu 2008a; Wu 2008b). The effects of water transfer on water quality improvement have drawn much attention, mainly focusing on the deduction of pollutants (Hu et al. 2008; Li et al. 2011; Hu et al. 2010). However, water transfer also causes serious sediment deposition along the river course, which leads to the degeneration of rivers and lakes and further decrease of their flood control capabilities. Water transfer-induced sediment problem has been less considered in previous research work (Yu et al. 2008). It is a challenging work to research cohesive sediment transport in complicated river networks.
In this study, a rainfall-runoff model was built to calculate the net rainfall of the plain areas and the discharge of mountain areas in the Taihu Basin, which form the lateral inflow and boundary discharge of the river course, respectively. The flow patterns of river networks were simulated utilizing a one-dimensional river network hydrodynamic model. Based on the boundary conditions of the flow in tributaries of the Wangyu River and the water level of Taihu Lake, a one-dimensional hydrodynamic and sediment transport numerical model of the Wangyu River was built to analyze the influences of the inflow rate of water transfer and the suspended sediment concentration (SSC) of inflow on the sediment distribution along the river course.
2 Study area
The Taihu Basin has a complicated river network system, with a total river length of 12 000 km and a river density of 3.24 km/km2(Fig.1) (Qin et al. 2007). The annual mean precipitation is 1 177 mm, and the mean volume of water resources is 1.77 × 1010m3(Wu 2008a). In 2005, the volume of water use was 3.54 × 1010m3, which shows the large gap between water supply and water need (Wu 2008b). Furthermore, economic developments have caused serious water pollution and, consequently, quality-related water scarcity. To improve the water quality and alleviate eutrophication, experimental water transfer from the Yangtze River to Taihu Lake has been carried out since 2002.

Fig. 1 Locations of Taihu Basin, drainage zones, and hydrological stations
The course of water transfer is from the Yangtze River to the Wangyu River, then to Taihu Lake, eventually flowing out of the lake via the Taipu River (Fig. 1). The Wangyu River, with a length of 60 km and a width of 72-90 m, is a key basin river for flood discharge and water transfer (Fig. 2). The Changshu hydro-junction, with a water gate and a water pump constructed and a design discharge of 180 m3/s, is located near the Yangtze River. The Wangting hydro-junction, an underground water gate located near Taihu Lake, connects the Wangyu River and Taihu Lake and passes through the Jinghang Canal underground. Water gates on the tributaries of the Wangyu River were constructed on their east side. There are also three storage lakes, Jialing Lake, Ezhen Lake, and Caohu Lake, along the Wangyu River, with areas of 0.9 km2, 16.2 km2, and 5.2 km2, respectively. As the tributaries of the Wangyu River are seriously polluted, the water gate of the Wangyu River connected to Taihu Lake isregulated according to the water quality of the Wangyu River (Hu et al. 2008). A Taipu River water gate is constucted to control the outflow rate according to the water level of Taihu Lake (Hu et al. 2010).
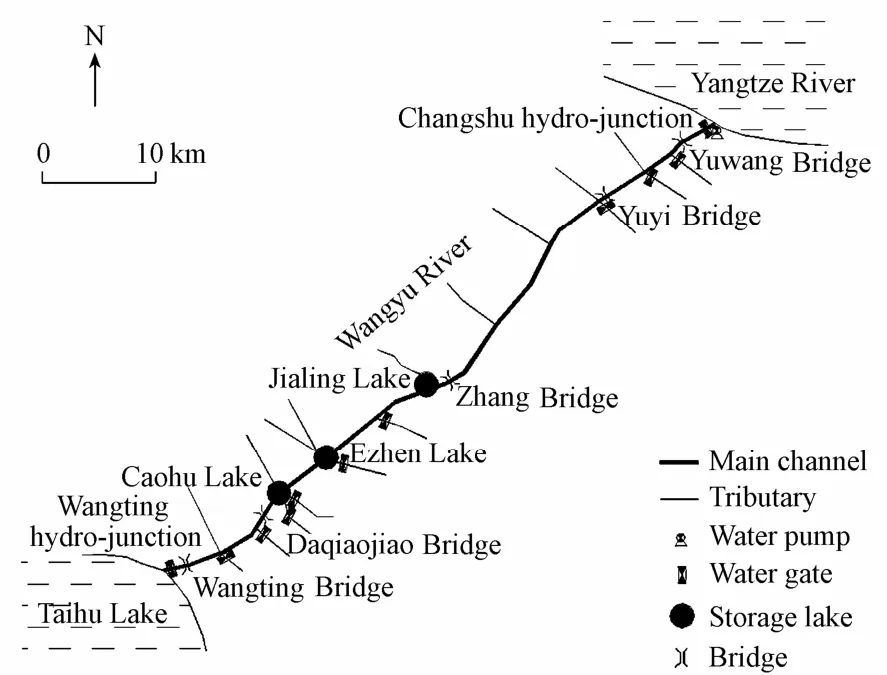
Fig. 2 Schematic diagram of Wangyu River and its tributaries, as well as observation cross-sections
Water transfer in 2003 started on August 6 and ended on November 17, with an average inflow rate of 1.066 × 107m3/d. A higher water inflow rate of 1.414 × 107m3/d occured within the periods of August 6 to 18 and August 25 to October 15. The highest water inflow rate of 2.43 × 107m3/d was observed on August 29. On August 21 and from November 4 to 5, the water transfer was stopped by reason of flood prevention and unsatisfying water quality, respectively. A total volume of 1.109 × 109m3of water was transfered into Taihu Lake through the Wangyu River, and 6.604 × 108m3of water flowed out of Taihu Lake via the Taipu River during the water transfer in 2003 (Hu et al. 2010).
The Xuliujing Station of the Yangze River is close to the entrance of the Wangyu River (Fig. 1), and thus the sediment features of the Xuliujing Station were adopted for reference. The observations at the Xuliujing Station from 1998 to 2001 show that the monthly mean SSC in the flood season, i.e., from July to October, is prominently higher than that in dry season (Table 1).
The entrance of the Wangyu River is situated on the southern side of the Yangtze River, where the observed SSC is less than the cross-section average SSC at the Xuliujing Station. During the water transfer in 2003, the hydrodynamic data and SSC along the Wangyu Riverwere observed for the periods of August 22 to 29 and October 11 to 16, and the average SSC values of the two periods were 0.059 kg/m3and 0.124 kg/m3, respectively. Table 2 shows the observed maximum and minimum median grain sizes (d50) of sediment at main cross-sections of the Wangyu River during water transfer in August, 2003. The meand50is 0.015 mm. The fraction of fine sediment is more than that of coarse sediment (Yu et al. 2008).
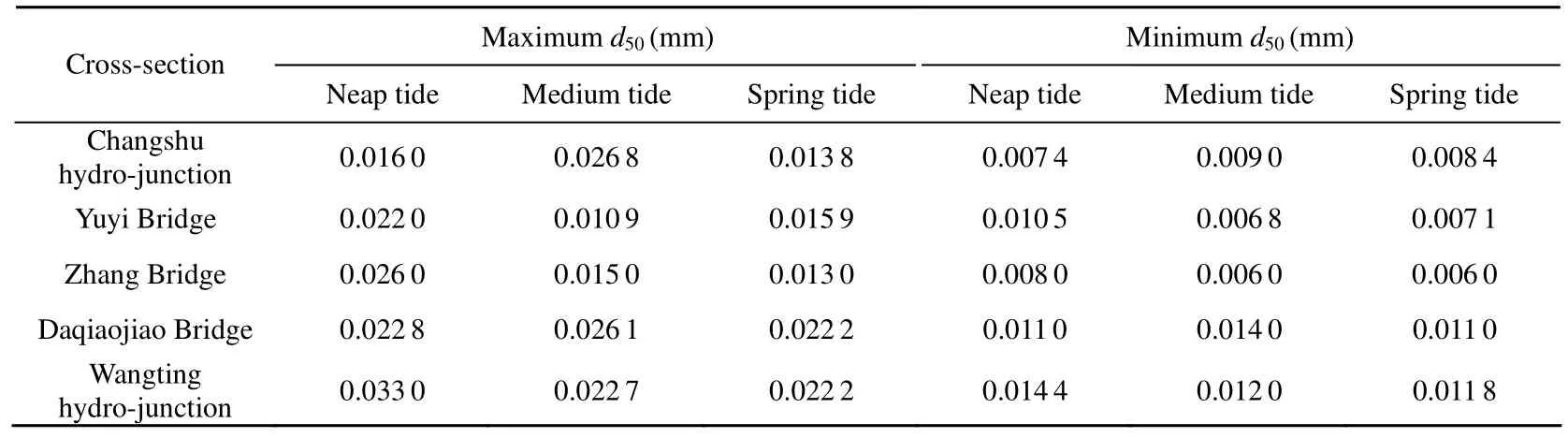
Table 2 Observedd50at main cross-sections during water transfer in August, 2003
3 Application of rainfall-runoff model
The Taihu Basin consists of 28 582 km2of plain areas and 8 313 km2of mountain areas. In terms of runoff yield and confluence patterns, Taihu Basin was divided into seven drainage zones, including Huxi (HX), Wuchengxiyu (WCXY), Yangchengdianmao (YCDM), Taihu Lake (TH), Hangjiahu (HJH), Zhexi (ZX), and Pudongxi (PDX) (Fig. 1). Between neighboring drainage zones, flood control facilities were constructed, including polders, water gates, water pumps, etc., to regulate flood discharges. The drainage zones of HX, ZX, and TH belong to the upstream region and others pertain to the downstream region. A rainfall-runoff model was developed based on the characteristics of underlying surfaces (Wang et al. 2007; Gong and Lin 2009). Runoff yield and confluence patterns for different kinds of underlying surfaces were considered, including water surfaces, paddy fields, arid lands, and lands for urban construction. These drainage zones were subdivided into a series of subzones with different ratios for different kinds of underlying surfaces (Table 3).
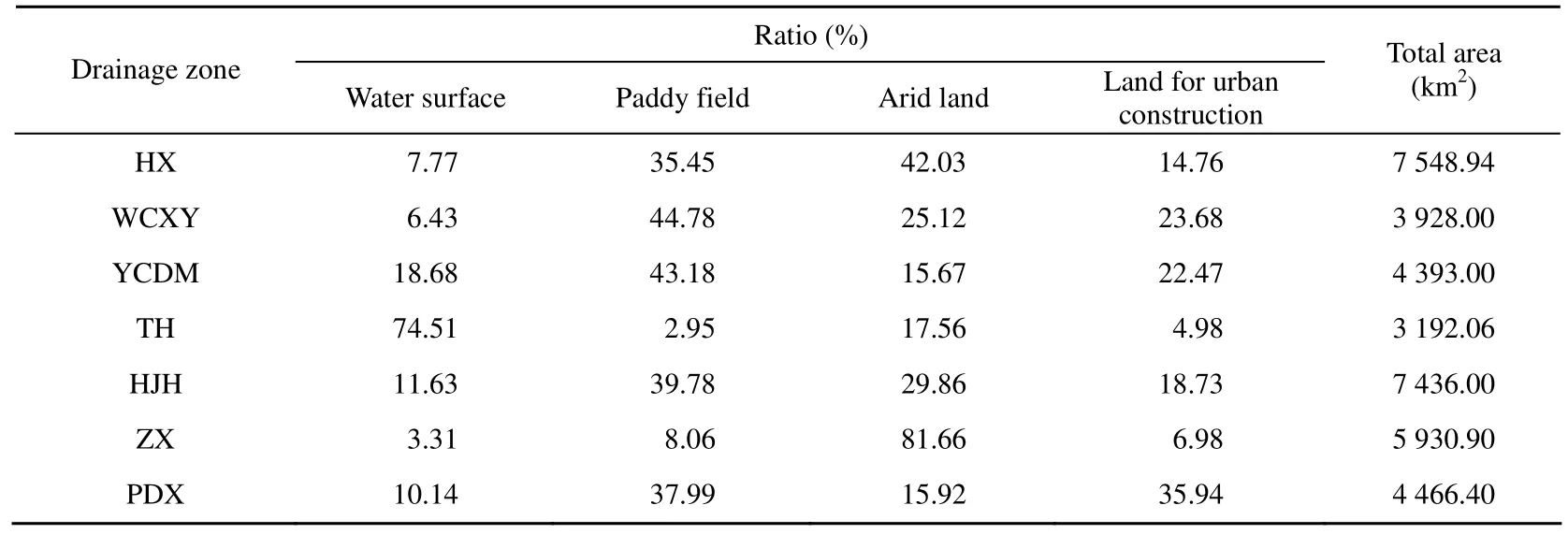
Table 3 Ratios of four kinds of underlying surfaces in each drainage zone
Precipitation and evaporation data for the Taihu Basin in 2003 were collected. The basin-averaged precipitation was 967 mm, 18% less than the long-term mean value, which shows that 2003 was a dry year, especially in Shanghai City and Zhejiang Province. The total runoff of 9.504 × 109m3, calculated by the rainfall-runoff model, agrees with the value of 9.53 × 109m3fromWater Resource Bulletin of Taihu Basin in 2003by the Taihu Basin Authority of Ministry of Water Resources, P. R. China (Table 4). The runoff in 2003 was 40.9% less than that of a normal year.

Table 4 Precipitation, evaporation and calculated runoff in 2003
4 1-D river network hydrodynamic numerical model
4.1 Model description
To simulate the flow patterns of river networks, a one-dimensional river network hydrodynamic numerical model was built based on the Saint-Venant equations:
The continuity equation is (Zhao 1984)

The momentum equation is (Zhao 1984)
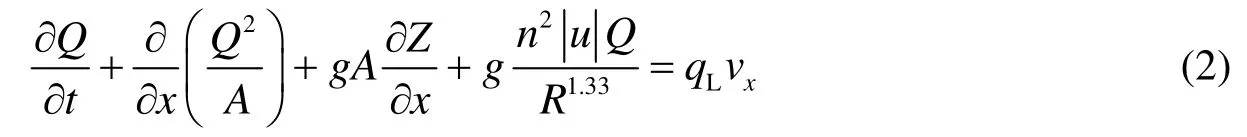
wherexis the longitudinal distance (m),Qis the discharge (m3/s),Zis the water level (m),qLis the lateral inflow for unit river length (m2/s),vxis the longitudinal component of the lateral inflow velocity (m/s),Ais the area of a cross-section (m2),Ris the hydraulic radius (m),uis the flow velocity (m/s),gis the acceleration of gravity (m/s2), andnis the Manning friction coefficient.
The finite differential equations were obtained by Preissmann’s four-point implicit differential scheme (Chen and Luo 1988; Zhu et al. 2001). From cross-sectionitoi+1 of a river segment, Eq. (1) and Eq. (2) can be written as
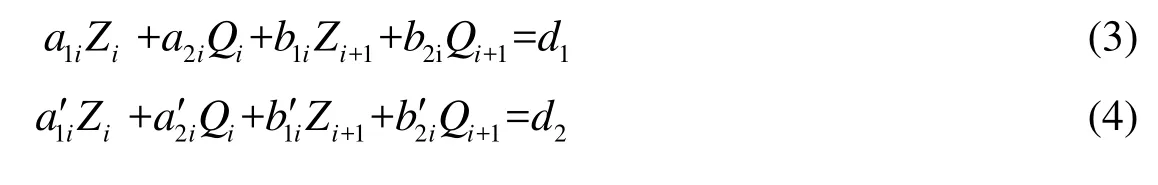

whereAi,Bi, andDiare known coefficient matrixes, andLiandLi+1are unknown column vectors.
The water level and discharge relationship between the first and last cross-sections of the river segment can be written as

where subscripts 1 andNrepresent the first and last cross-sections, respectively. Coefficient matrixesSandTcan be calculated based on the recurrence relations between cross-sectionsiandi+1 in Eq. (5).
The hydraulic conditions at the junction of river networks were determined based on the mass conservation and energy conservation rules. The mass conservation rule means that discharge changes are equal to water storage variations at a certain junction. Assuming no change of water storage, it can be approximated as follows:

whereQinandQoutare the inflow and outflow of intersecting river courses, respectively.
The energy conservation rule (Akan and Yen 1981) is approximated by a kinematic compatibility condition as

whereZinand Zoutare the water levels at inflow and outflow cross-sections of intersecting river courses, respectively. With the boundary water level and discharge, the water level and discharge of each cross-section can be calculated using the substructure method (Zhao 1984).
4.2 Model validation
The river networks were schematized as 1 390 segments, 1 049 junctions, and 4 157 crosssections. In the model, 42 boundary tide level processes along the Yangtze River and the Hangzhou Bay were considered, seven of which were observed tide level processes, and the rest were obtained by Lagrangian interpolation. The net rainfalls of plain areas calculated by the rainfall-runoff model were taken as the lateral inflow of river segments, the calculated discharges of moutain areas were used as the inflow boundary condition of river networks, and the Manning friction coefficientnwas set to be 0.02-0.03.
The one-dimensional river network hydrodynamic model and the rainfall-runoff model were synthetically validated with the water transfer scenario in 2003. This involved daily-averaged water level processes of Taihu Lake and Ganlu, Wangmuguan, Wuxi, Chenmu, and Jiaxing Stations in August (Fig. 1). The water level of Taihu Lake was calculated by averaging the tide level of the five stations around the lake. The calculated and observed waterlevels are shown in Fig. 3, which demonstrates that except at Jiaxing Station, simulations agree well with observations. The reason for the discrepancy between simulations and observations at Jiaxing Station is that the observed water level obtained from the forecasting station has not been corrected.
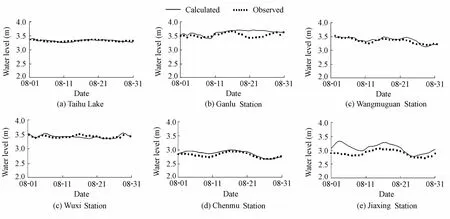
Fig. 3 Calculated and observed daily-averaged water level processes in August, 2003
5 1-D hydrodynamic and sediment transport numerical model
Sedimentation induced by the water transfer from the Yangtze River to Taihu Lake mainly occurs in the Wangyu River. To simulate the sediment transport in the Wangyu River, a one-dimensional hydrodynamic and sediment transport numerical model was built based on the HEC-RAS software, developed by the Hydrologic Engineering Center of the U.S. Army Corps of Engineers. The HEC-RAS software is a strong tool for simulating one-dimensional steady or unsteady flow, sediment transport, and bed evolution. In this study, one-dimensional unsteady hydrodynamic and cohesive sediment transport modules were involved.
5.1 Model description
As with the one-dimensional river network hydrodynamic numerical model (Eq. (1) through Eq. (8)), a system of linear equations that can be solved for each time step was deduced by adopting the internal and external boundary conditions:

whereAis the coefficient matrix,Xis the column vector of unknowns, andBis the column vector of constants. A skyline storage scheme (Bathe and Wilson 1976) was used to store the sparse coefficient matrix efficiently, and Gaussian elimination was utilized to solve the simultaneous equations.
The sediment continuity equation is given as

whereWis the channel width (m),Zbis the bed elevation (m),λpis the active layer porosity,tis time (s), andQsis the sediment transport load (m3/s).
The observed meand50of sediment was 0.015 mm during the water transfer in 2003, thus falling into the category of cohesive sediment. Cohesive particles are small enough that their behaviors are usually dominated by surface forces rather than gravity, and therefore the commonly used sediment transport equations (Dou 1963; Zhang et al. 2007), which calculate the sediment erosion and deposition according to the sediment carrying capacity of flow, are not suitable for the current research. Thus, the Krone and Parthenaides equations were used to quantify the deposition and erosion of cohesive sediment (van Ledden and Wang 2001). For cohesive sediment, suspended load transport was considered instead of bed load transport (van Rijn 1993).
The deposition equation for simulating cohesive sediment transport (Krone 1962) is

whereCis the SSC value (kg/m3),τbis the bed shear stress (N/m2),τcis the critical bed shear stress for deposition (N/m2),ωis the settling velocity (m/s), andyis the water depth (m).
The erosion eq uation (Parthenaides 1962; Parthenaides 1965) is

wheremis the mass of sediment in a water column (kg),τc′ is the critical bed shear stress for erosion (N/m2), andMis the empirical erosion coefficient (kg/(m2·s)).
5.2 Model validation
The Wangyu River was schematized as 13 river segments, 20 tributaries, and three storage lakes (Fig. 2). The observed tide level and SSC at the Changshu hydro-junction, the water level of Taihu Lake, and the flow rate of tributaries calculated by the one-dimensional river network numerical model were taken as boundary conditions. In the model, the settling velocity is 0.4 mm/s, the critical bed shear stress for deposition is 0.2 N/m2, the critical bed shear stress for deposition is 0.1 N/m2, and the erosion coefficient is 5 × 10-5kg/(m2·s).
The model was validated by the observed SSC processes at every 4-h interval at four cross-sections of the Wangyu River during the periods of 16:00 on August 22 to 19:00 on August 23 (neap tide), 9:00 on August 25 to 11:00 on August 26 (medium tide), and 12:00 on August 28 to 14:00 on August 29 (spring tide), 2003. The cross-sections were the Yuyi Bridge, Zhang Bridge, Daqiaojiao Bridge, and Wangting Bridge (Fig. 2). The calculated and observed SSC values of the spring tide are shown in Fig. 4. At cross-sections of the Yuyi Bridge and Zhang Bridge, the calculated SSC values are greater than the observations, which may be dueto improper selection of the parameters in simulation. After the sedimentation in the three storage lakes, the calculated SSC values get closer to the observations at the Daqiaojiao Bridge and Wangting hydro-junction. In addition, SSC is greatly associated with the flow patterns of tributaries. Therefore, the flow patterns of tributaries should be reasonably controlled in the model so as to get better agreements.
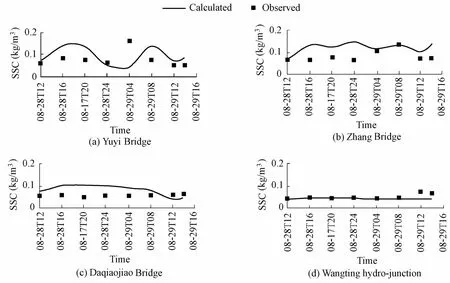
Fig. 4 Calculated and observed SSC values of spring tide in August, 2003
6 Results and discussion
Case studies were carried out by varying one parameter at a time to analyze the influence of other factors on the sediment distribution. The parameters included the water transfer inflow rate and SSC of inflow, and the values of the parameters for different cases are shown in Table 5. The water transfer duration from August 1 to August 31, 2003 was assumed in the following study. To bring the case studies closer to the reality, constant water transfer inflow rates of 0.9 × 107m3/d and 1.6 × 107m3/d, representing water transfer by gravity and pumping, respectively, were imagined. Constant SSC values of 0.1 kg/m3and 0.2 kg/m3were imagined for the lower and higher cases, respectively.

Table 5 Imagined cases of water transfer in Wangyu River
The simulated SSC at main cross-sections of the Wangyu River is shown in Table 6. The relative distances from the Yuwang Bridge, Yuyi Bridge, Zhang Bridge, and Wangting Bridge to the Changshu hydro-junction are 3.9 km, 18.1 km, 31.8 km, and 55.9 km, respectively (Fig. 2). Comparison of the simulated results of case 1 and case 2 shows that a lower watertransfer inflow rate leads to a higher sediment deposition and a more rapid decrease of SSC. SSC decreases by approximately 50% at the Yuyi Bridge in case 1, unlike at the Zhang Bridge in case 2, which is 13.7 km downstream of the Yuyi Bridge. Although the SSC values of inflow in case 2 and case 3 are different, the decrease rates of SSC are almost the same. The higher the inflow rate or SSC of inflow is, the higher the SSC value is at a certain cross-section of the Wangyu River.
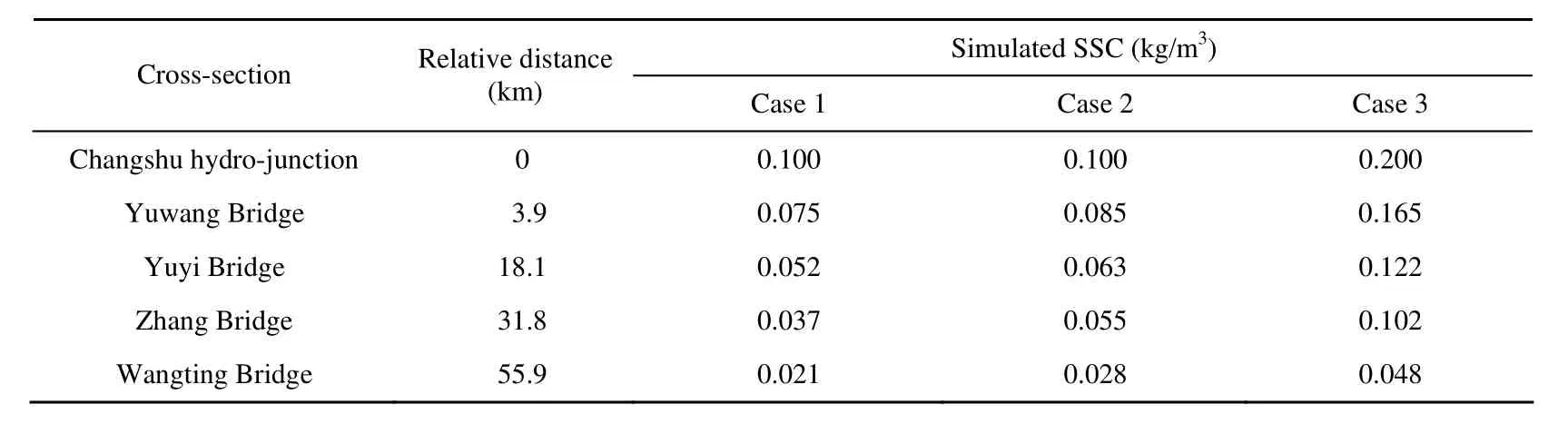
Table 6 Simulated SSC at main cross-sections of Wangyu River
The sediment deposition along the Wangyu River is shown in Fig. 5. Assuming a dry sediment density of 500 kg/m3, the corresponding sedimentation thickness was calculated, which is shown in Fig. 6. As shown in Fig. 5, when sediment is transferred into the Wangyu River, it deposits rapidly due to a sharp decrease of the flow velocity. Therefore, the sedimentation per kilometer and sedimentation thickness at the cross-section near the Changshu hydro-junction reach their maximum values, about 1.1 × 103-2.3 × 103t/km and 2.5-5 cm for different cases, respectively. With an increasing distance from the Changshu hydro-junction along the Wangyu River, the sediment deposition and sedimentation thickness decrease gradually. A weak current in the Wangyu River causes deposition in any case. In comparison with the relatively lower inflow rate in case 1, the higher inflow rate in case 2 leads to a higher sediment deposition per kilometer and sedimentation thickness, and so does the higher SSC in case 3 compared with the relatively lower SSC in case 2.

Fig. 5 Sediment deposition along Wangyu River
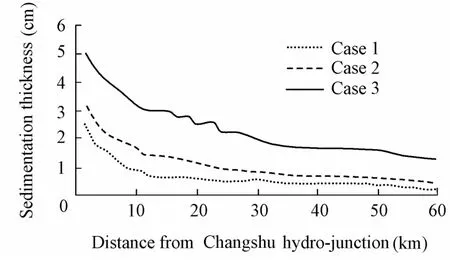
Fig. 6 Sedimentation thickness along Wangyu River
The cumulative percentage of sedimentation in the Wangyu River is shown in Fig. 7, in which the deposition in storage lakes is excluded. The sediment distributions in river networks, including total sediment input in the Wangyu River, deposition in the river course, deposition in the storage lakes, and sediment output to Taihu Lake, are listed in Table 7. The sharpdecrease of flow velocity at the upper river course causes a high ratio of sedimentation. Approximately 40% of total sediment input is deposited within the upper reach of the Wangyu River (30 km from the Changshu hydro-junction), whereas 20% is deposited within the lower reach. The flow velocity in case 1 is the lowest of the three cases, which leads to the highest cumulative percentage of sedimentation within the upper Wangyu River. The cumulative percentage of sedimentation in case 3 is the highest within the lower river course because of the higher SSC of inflow. Considering the amount of sedimentation in storage lakes, the percentage of sediment output to Taihu Lake in case 3 is the lowest (30.6%), and the value in case 1 is slightly lower than that in case 2, accounting for 36.3% and 38.4%, respectively.

Fig. 7 Cumulative percentage of sedimentation along Wangyu River excluding deposition in storage lakes

Table 7 Sediment distribution in river networks 103t
7 Conclusions
The scenario of water transfer in 2003 from the Yangtze River to the Taihu Basin was studied. A rainfall-runoff model was built and the runoff of 2003 was calculated. The flow patterns of river networks were simulated using a one-dimensional river network hydrodynamic numerical model. The observations of the water level and SSC were employed to synthetically validate the models. Taking the flow of tributaries and the water level of Taihu Lake as boundary conditions, a one-dimensional hydrodynamic and sediment transport numerical model of the Wangyu River was built to analyze the influence of the water transfer inflow rate and SSC of inflow on sediment transport. Three cases were imagined, with input rates of 0.9 × 107m3/d, 1.6 × 107m3/d, and 1.6 × 107m3/d, and constant SSC values of 0.1 kg/m3, 0.2 kg/m3, and 0.2 kg/m3, respectively.
The water transfer inflow rate and SSC of inflow have significant effects on the sediment distribution. Generally speaking, a weak current in the water transfer river course causes deposition. The higher the inflow rate or SSC of inflow is, the higher the SSC value is at a certain cross-section of the river course. In comparison with SSC of inflow, the inflow rate haslarger effects on the decrease rate of SSC along the river course. Higher inflow rate and SSC of inflow contribute to higher sediment deposition per kilometer and sediment thickness.
A sharp decrease of inflow velocity induces intense sedimentation at the cross-section near the Changshu hydro-junction, i.e., the sediment deposition per kilometer and sedimentation thickness reach maximum values. Moreover, with an increasing distance from the Changshu hydro-junction along the river course, the sediment deposition and sedimentation thickness decrease gradually. In this study, approximately 40% of total sediment input was deposited within the upper reach of the Wangyu River, whereas only 20% was deposited within the lower reach, if the deposition in storage lakes was excluded.
In this study, the assumed low SSC of inflow and inflow rate of water transfer led to insignificant deposition in the river course, i.e., the maximum sedimentation per kilometer and sedimentation thickness over one month near the Changshu hydro-junction were only about 1.1 × 103-2.3 × 103t/km and 2.5-5 cm, respectively. However, water transfer is expected to be a long-term strategy, and the cumulative sedimentation following water transfer would seriously impact the sustainable development of the river course. Thus, further research on long-term evolution of river networks after water transfer is needed.
Akan, A. O., and Yen, B. C. 1981. Diffusion-wave flood routing in channel networks.Journal of the Hydraulics Division, 107(6), 719-732.
Bathe, K. J., and Wilson, E. L. 1976.Numerical Methods in Finite Element Analysis. Englewood Cliffs: Prentice-Hall Inc.
Chen, X. W., and Luo, Z. S. 1988. Computation of flow and suspended sediment in network channel of tidal river.Hydro-science and Engineering, (1), 33-41. (in Chinese)
Dong, X., Bennion, H., Battarbee, R., Yang, X., Liu, E., and Yang, H. 2008. Tracking eutrophication in Taihu Lake using the diatom record: Potential and problems.Journal of Paleolimnology, 40(1), 413-429. [doi: 10.1007/s10933-007-9170-6]
Dou, G. R. 1963. Sediment movement and riverbed deformation computation in tide current.Journal of Hydraulic Engineering, (4), 13-24. (in Chinese)
Gong, Z., and Lin, Z. X. 2009. Strategy of flood control in Taihu Basin.Advances in Water Resources and Hydraulic Engineering, Proceedings of 16th IAHR-APD Congress and 3rd Symposium of IAHR-ISHS, Vol. III, 1011-1016. Beijing: Springer. [doi:10.1007/978-3-540-89465-0_177]
Hu, L. M., Hu, W. P., Zhai, S. H., and Wu, H. Y. 2010. Effects on water quality following water transfer in Lake Taihu, China.Ecological Engineering, 36(4), 471-481. [doi:10.1016/j.ecoleng.2009.11.016]
Hu, W. P., Zhai, S. H., Zhu, Z. C., and Han, H. J. 2008. Impacts of the Yangtze River water transfer on the restoration of Lake Taihu.Ecological Engineering, 34(1), 30-49. [doi:10.1016/j.waters.2009.11.003]
Huang, F., Wang, X. Q., Lou, L. P., Zhou, Z. Q., and Wu, J. P. 2010. Spatial variation and source apportionment of water pollution in Qiantang River (China) using statistical techniques.Water Research, 44(5), 1562-1572. [doi:10.1016/j.watres.2009.11.003]
Jiang, Y. 2009. China’s water scarcity.Journal of Environmental Management, 90(11), 3185-3196. [doi: 10.1016/j.ecoleng.2009.04.016]
Krone, R. B. 1962.Flume Studies of the Transport of Sediment in Estuarial Shoaling Processes. Berkeley: Hydraulic Engineering Laboratory and Sanitary Engineering Research Laboratory, University of California.
Li, Y. P., Acharya, K., and Yu, Z. B. 2011. Modeling impacts of Yangtze River water transfer on water ages inLake Taihu, China.Ecological Engineering, 37(2), 325-334. [doi:10.1016/j.ecoleng.2010.11.024]
Partheniades, E. 1962.A Study of Erosion and Deposition of Cohesive Soils in Salt Water. Ph. D. Dissertation. Berkley: University of California.
Partheniades, E. 1965. Erosion and deposition of cohesive soils.Journal of the Hydraulics Division, 91 (HY1), 105-139.
Pu, P. M., Hu, W. P., Yan, J. S., Wang, G. X., and Hu, C. H. 1998. A physico-ecological engineering experiment for water treatment in a hypertrophic lake in China.Ecological Engineering, 10(2), 179-190. [doi:10.1016/S0925-8574(98)00017-2]
Qin, B. Q., Xu, P. Z., Wu, Q. L., Luo, L. C., and Zhang, Y. L. 2007. Environmental issues of Lake Taihu, China.Developments in Hydrobiology, 194, 3-14. [doi:10.1007/978-1-4020-6158-5_2]
Schwartz, J. 2003. The impact of state capacity on enforcement of environmental policies: The case of China.The Journal of Environment and Development, 12(1), 50-81. [doi:10.1177/1070496502250438]
van Ledden, M., and Wang, Z. B. 2001. Sand-mud morphodynamics in an estuary.Proceedings of the 2nd IAHR symposium on River, Coastal and Estuarine Morphodynamics (RCEM2001). New York: Springer.
van Rijn, L. C. 1993.Principles of Sediment Transport in Rivers, Estuaries and Coastal Seas. Amsterdam: Aqua Publications.
Wang, C. H., Wang, J., Cheng, W. H., and Zhu, Y. 2007. Numerical simulation of runoff yield and confluence in plain area.Journal of Hohai University (Natural Sciences), 35(6), 627-632. (in Chinese)
Wang, Q. G., Gu, G., and Higano, Y. 2006. Toward integrated environmental management for challenges in water environmental protection of Lake Taihu Basin in China.Environmental Management, 37(5), 579-588.
Wu, H. Y. 2008a. Study on key technologies of Yangtze-Taihu water diversion.China Water Resources, (1), 6-8. (in Chinese)
Wu, H. Y. 2008b. Practice and exploration on maintenance of river-lake eco-system health for Taihu Basin with project of water division from Yangtze River to Taihu Lake.Water Resources and Hydropower Engineering, 39(7), 4-8. (in Chinese)
Yang, G. S., and Wang, D. J. 2003.Economical Development, Water Environment and Water Calamity of Taihu Basin. Beijing: Science Press. (in Chinese)
Yu, X. Z., Peng, Q. D., Liao, W. G., and Zhang, H. J. 2008. Simulation of sedimentation in Yangtze-Taihu Water Diversion.China Water Resources, (1), 34-36. (in Chinese)
Zhang, R. J., Xie, J. H., and Chen, W. B. 2007.River Dynamics. Wuhan: Wuhan University Press. (in Chinese)
Zhao, S. Q. 1984. Calculation of tidal currents in channel networks.Hydro-science and Engineering, (1), 40-51. (in Chinese)
Zhu, L. Z., Chen, Y. Y., and Zhou, R. B. 2008. Distribution of polycyclic aromatic hydrocarbons in water, sediment and soil in drinking water resource of Zhejiang Province, China.Journal of Hazardous Materials, 150(2), 308-316. [doi:10.1016/j.jhazmat.2007.04.102]
Zhu, Y. L., Yan, Y. X., Jia, L. W., and Mao, L. H. 2001. Numerical model of unsteady flow and suspended-sediment transport in river networks with junction control method.Journal of Hydrodynamics, 16(4), 503-510. (in Chinese)
This work was supported by State Key Development Program of Basic Research of China (Grant No. 2010CB429001), the National Natural Science Foundation of China (Grant No. 51009062), and the Special Fund of Hydrology-Water Resources and Hydraulic Engineering (Grant No. 2009586812).
*Corresponding author (e-mail:ckzhang@hhu.edu.cn)
Received Feb. 25, 2011; accepted Oct. 11, 2011
 Water Science and Engineering2011年4期
Water Science and Engineering2011年4期
- Water Science and Engineering的其它文章
- Two-dimensional physical habitat modeling of effects of habitat structures on urban stream restoration
- Experimental study on total dissolved gas supersaturation in water
- Hydrodynamic effects of reconnecting lake group with Yangtze River in China
- Research on shape optimization of CSG dams
- Analysis of black water aggregation in Taihu Lake
- Large eddy simulation of water flow over series of dunes
