锯齿型石墨烯纳米带的能带研究*
王雪梅 刘 红
(南京师范大学物理科学与技术学院,南京 210046)(2010年5月24日收到;2010年7月7日收到修改稿)
锯齿型石墨烯纳米带的能带研究*
王雪梅 刘 红
(南京师范大学物理科学与技术学院,南京 210046)(2010年5月24日收到;2010年7月7日收到修改稿)
运用π电子紧束缚模型,具体研究了锯齿型石墨烯纳米带(ZGNRs)的边界结构对能带,特别是费米面附近的导带和价带电子的影响.计算了七种不同边界结构的ZGNRs的能带色散关系及费米面附近价带电子在原胞中各原子上的分布情况.计算结果表明:两边界都无悬挂原子的NN-ZGNRs,只有一边界有悬挂原子的 DN-ZGNRs,两边界都有五边形环的SPP-ZGNRs和ASPP-ZGNRs为金属性.两边界都有悬挂原子的DD-ZGNRs,一边界为五边形环另一边界无悬挂原子的PN-ZGNRs和一边界为五边形环另一边界有悬挂原子的PD-ZGNRs都为半导体性,但是随纳米带宽度的增加,DD-ZGNRs和PD-ZGNRs的带隙很快减小至零,而PN-ZGNRs的带隙随宽度呈指数衰减至一个有限值0.154 eV.结果也显示出不同边界结构对费米面附近价带上电子分布产生的影响不同,在石墨烯边界原子上电子概率都相对较高.
锯齿型石墨烯纳米带,紧束缚模型,电子密度分布,缺陷结构
PACS:71.15.Ap,71.20.Tx
1.引 言
自从2004年Novoselov等人[1]成功制备单层石墨(石墨烯,Graphene)以来,石墨烯以其独特的电学性质,如 Klein 隧穿[2],狄拉克颤动[3],半整数霍尔效应[4—6]等引起了科学家们的广泛关注.在科技迅猛发展的今天,石墨烯已经成为一种新型的碳纳米材料,并且由其制备出了许多纳米尺寸的石墨器件,如量子结[7—9],双层石墨结构[10—12],石墨烯纳米带(graphene nanoribbons,GNRs)[13—15]等,它们具有巨大的应用前景.石墨烯纳米带作为一种准一维碳纳米材料,几何结构是决定电子结构的主要因素,在实际应用中具有强烈的边界效应和复杂的电学性质,因此对石墨烯纳米带几何结构的研究具有重要的意义.根据边界结构不同,石墨烯纳米带主要分为边界呈锯齿状的锯齿型石墨烯纳米带(ZGNRs)和边界呈扶手椅状的扶手椅型石墨烯纳米带(AGNRs).
对于石墨烯纳米带电子结构的理论研究,方法主要有第一性原理的密度泛函理论[16—18],狄拉克方程[19,20]和紧束缚理论[21—23]等.根据第一性原理计算结果显示[16],无论是锯齿型还是扶手椅型石墨烯纳米带(边界悬氢)都有能隙,具有半导体性,但两者带隙产生的原因有所不同.Barone等人[17]计算得到,扶手椅型石墨烯纳米带的带宽尺寸越大,能隙振荡的幅值越来越小;不同手性的石墨烯纳米带,手性角度越大,宽度越大,则能隙越小.Son等人[18]计算得到不考虑自旋极化时锯齿型石墨烯纳米带为金属性的,而考虑了自旋极化时锯齿型石墨烯纳米带能隙打开,为半导体性.由紧束缚模型计算得到的结果显示锯齿型石墨烯纳米带(边界悬氢)具有金属性[23],而对于扶手椅型石墨烯纳米带(边界悬氢),原胞中碳原子数为2N,当 N+1=3q(q为整数)时为金属性,其他情况为半导体[22].狄拉克方程计算结果[19]与紧束缚理论计算结果相似.Han等人[24]通过实验发现,不同宽度、不同晶格取向的石墨烯纳米带,都具有半导体性,且带隙的大小与宽度成反比.实验结果和理论计算之间还存在很大的差别.Ouyang等人[25]还研究了空位缺陷对石墨烯纳米带电子结构的影响,发现空位缺陷的引入导致扶手椅型石墨烯纳米带半导体到金属的转变和锯齿型石墨烯纳米带导电性的变化.同时,Rozhkov等人[21]报道边界结构的影响非常重要,边界处键长的无序会导致扶手椅型石墨烯纳米带由金属到半导体的转变.因此对于石墨烯能带的研究还有必要做更细致深入的分析和计算,特别是边界结构对石墨烯能带影响的研究.
在以往的紧束缚能带理论方法中,大多是以两个原子构成石墨小原胞,加入边界条件,推导出能带的解析表达式.本文完全将石墨烯纳米带作为一维材料考虑,以其一维方向的周期单元为大原胞.该原胞尺寸相对于石墨原胞更大,更易于直观地分析能带结构中对电学性质有主要贡献的电子的分布情况.对于锯齿型石墨烯,由于边界存在不稳定的悬挂碳原子,因此在计算能带时,如何处理悬挂原子是一个重要的问题.通常在密度泛函理论计算中,采用氢原子饱和该悬挂原子上的电子.在本文中,我们考虑在实际实验中,石墨烯并不是处于含氢的环境中,且已有实验观察到边界悬挂碳原子的这种缺陷结构对石墨烯电子输运性质有很大影响[26],所以本文不采用边界悬挂氢原子的方法,而直接计算边界存在悬挂碳原子的结构对石墨烯能带结构的影响.另外,对于边界上的悬挂原子,我们根据sp2轨道杂化的特点,考虑将相邻的两个悬挂键构成五边形环,使石墨烯结构趋于稳定.这与运用分子动力学模拟与第一性原理的方法计算发现ZGNRs边界易于形成能量较低的五边形结构[27]的结论一致.因此本文计算了锯齿型石墨烯纳米带在边界有无悬挂碳原子和五边形环的七种不同边界结构下的能带色散关系,讨论石墨烯纳米带的边界结构和尺寸对电学性质的影响.
2.石墨烯纳米带的紧束缚能带理论方法
本文采用紧束缚近似,系统的哈密顿量可表示为

3.不同边界结构 ZGNRs的紧束缚能带结构和结果讨论
根据上述理论方法,下面我们针对不同边界、不同尺寸的ZGNRs,计算它们的能带色散关系以及费米面附近价带上电子在原胞中各原子上的密度分布情况.
对于图1(a)所示NN-ZGNRs的结构(以字母N表示边界没有悬挂原子和五边形环结构),晶格常数为,其结构沿中轴线对称.石墨烯纳米带的能带结构显示于图1(d)中,在费米能EF=0处,无能隙,且态密度不为零,见图1(c)所示,故 NNZGNRs表现为金属性特征,这与 Brey等[19]的狄拉克方程计算的结果和 Ezawa[23]的紧束缚模型计算的结果相符.费米波矢kF=±0.5处,费米速度vF≈0.对于不同波矢状态,费米面附近价带上电子在原胞中各原子上的密度分布,见图1(b)所示.对于费米波矢kF=±0.5的状态上,可以观察到边界原子8上的电子密度等于1.由于能量在此处是简并的,而此处与价带能量简并的导带上电子在各原子上的密度分布图显示了,在费米波矢 kF=±0.5处,1原子上的电子密度为1.说明对于具有此种边界结构的ZGNRs,其费米电子全部分布在边界原子1,8上.由于该状态上有两个电子,分别为自旋向上和自旋向下,根据铁磁自旋波理论[28]及密度泛函计算结果[18]显示,自旋向上和自旋向下电子的相互作用为铁磁相互作用,且在同一个带边上分布的π电子自旋方向一致时,能量较低.而 ZGNRs的两个不同边界上电子具有相反的自旋方向,存在相反磁矩,故呈现出反铁磁结构.我们进一步计算了此种边界结构不同宽度的石墨纳米带的能带结构,发现导电电子集中分布在两个边界原子上且分别具有不同的自旋状态.因此可以通过替代式掺杂[29]或者加入外电场[18]来改变电子的自旋分布,设计制作一种自旋阀器件,从而控制自旋输运.这些工作已经引起人们的广泛关注.
DN-ZGNRs(以字母D表示一边界原子悬挂)的结构见图2(a)所示,晶格常数为,原胞中 1原子悬挂在边界上.其能带结构和电子态密度见图2(d)和(c),费米能EF=0处是一个平坦的能带,具有非常高的电子态密度,而且此能带是被电子半充满的,因此具有此种边界结构的DN-ZGNRs的电导呈现出金属特性.对于平坦的导带,任意波矢状态下的费米速度vF=0.费米面附近价带上电子在原胞中各原子上的密度分布如图2(b)所示,不同的波矢状态上电子密度分布差别较大.对于状态kF=0的Γ点,电子主要分布在DN-ZGNRs边界处的悬挂原子1上,从3原子到9原子,奇数原子上电子密度依次降低到零;然而对于状态kF=±0.5,电子全部分布在DN-ZGNRs另一边界的非悬挂原子9上;偶数原子上的电子密度在各波矢状态下都为零.尽管不同波矢状态上电子分布差别较大,但是我们仍能看出导电电子主要分布在两个边界上.由于费米能处的平坦能带为电子半充满的,我们不是很清楚对电导起主要作用的电子如何分布在两个边界上.为此我们可以设想加入一些外场或微扰相互作用,使得此平坦能带劈裂为两个子能带,从而能够进一步分析导电电子在边界上的分布特点,研究此种边界结构对电导性质的影响及控制作用.
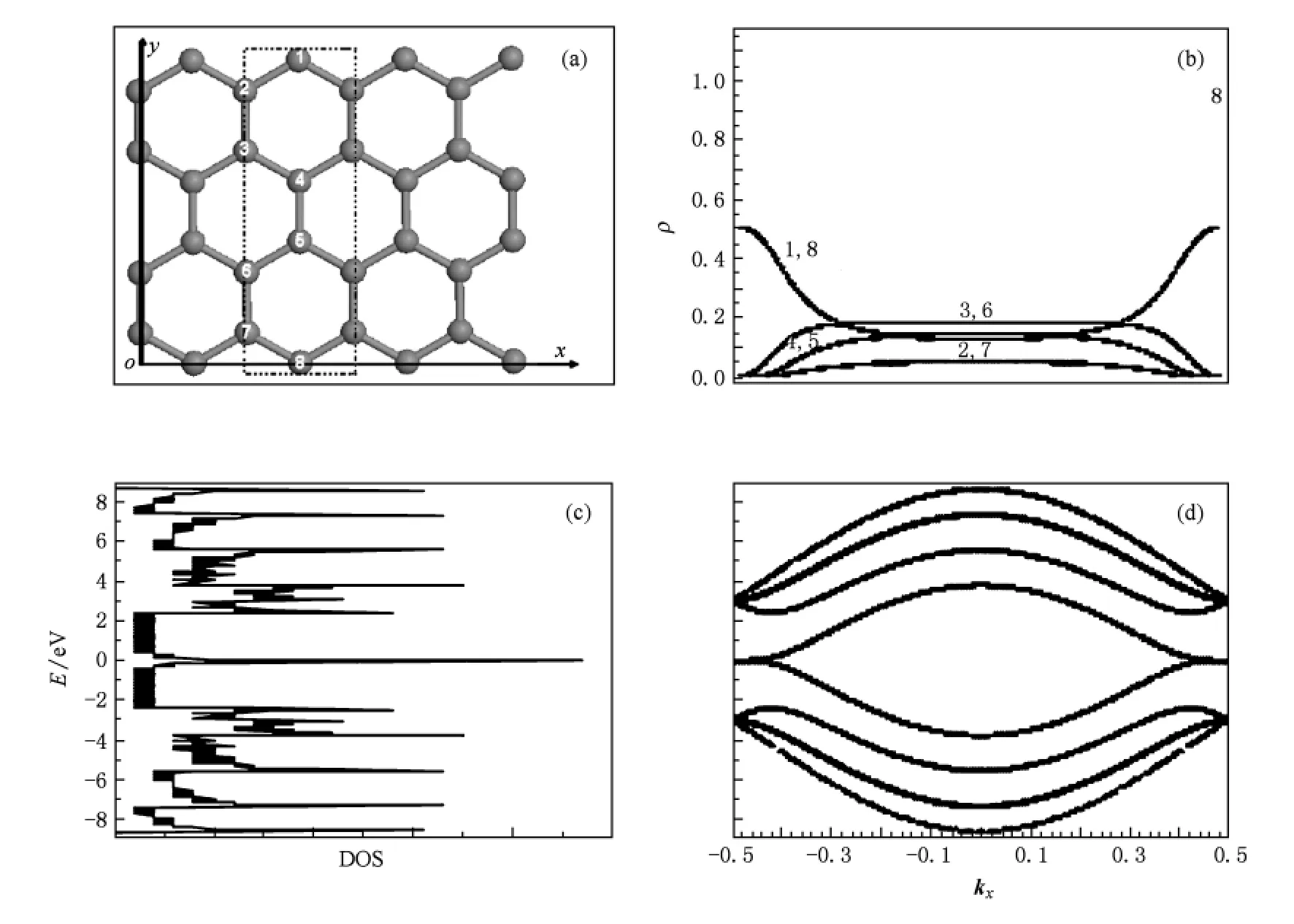
图1 NN-ZGNRs原胞含8个原子的几何结构和电子结构 (a)NN-ZGNRs的几何结构示意图,其中虚线框表示原胞;(b)NN-ZGNRs费米面附近价带上电子在原胞中各原子上的密度分布;(c)NN-ZGNRs的电子态密度;(d)NN-ZGNRs的能带结构

图2 DN-ZGNRs原胞中含9个原子的几何结构和电子结构 (a)DN-ZGNRs的几何结构示意图,其中虚线框表示原胞;(b)费米能EF=0处,对于平坦导带,在各波矢状态上电子在原胞中各原子上的密度分布;(c)DN-ZGNRs的电子态密度;(d)DN-ZGNRs的能带结构
如果在图2(a)DN-ZGNRs的结构基础上,考虑边界上悬挂的两个碳原子成键,构成边界为五边形缺陷环结构的PN-ZGNRs(以字母P表示一边界为五边形环结构),见图3(a)所示.因只考虑缺陷结构的影响,本文中缺陷环上的键长仍为原键长.原胞内原子数 N=18,晶格常数为,此时 PNZGNRs两边界都无悬挂原子.其能带结构和电子态密度分别显示于图 3(d)和(c),其中导带底在-0.06≤kx≤0.06范围内是平坦的,对应的能量为0 eV,而价带顶在波矢 kx=±0.24处,对应能量为-0.90 eV,故能隙为Eg=0.90 eV.由于导带底的位置与价带顶的位置不同,故此种结构的PN-ZGNRs为间接半导体.对于不同波矢状态,最高价带上电子在原胞中各原子上的密度分布见图3(b).对于Γ点kx=0的状态,电子主要分布在PN-ZGNRs边界五边形缺陷环中的3,4原子上,1,2原子上的电子密度比3,4原子上的电子密度小,而其它原子上电子密度为零;对于kx=±0.5处,相对于其他原子,五边形缺陷环中的6原子上的电子密度较大.与结构为DN-ZGNRS的能带结构图、电子密度分布图2(d),(b)比较,进一步分析得,由于 PN-ZGNRs的边界五边形环的结构畸变,使能带结构发生巨大变化,原来导带价带对称的能带结构转变为非对称的能带结构,导电性也由金属性转变为半导体性,导电电子分布从原来集中于边界原子上,分散到PNZGNRs边界五边形缺陷环的5个原子上.
在图4(a)DD-ZGNRs的结构基础上,考虑1,2原子成键,19,20原子仍悬挂,形成 PD-ZGNRs结构,见图5(a)所示.原胞中原子数N=20,晶格常数为.石墨烯能带结构与电子态密度如图4(d),(c)所示,靠近能量E=0处,导带底能量为 E=0.01 eV,位于 Γ点,价带顶能量为 E=-0.09 eV,在波矢kx=±0.5处,不在同一 k点,能隙 Eg=0.1 eV,此种结构的PD-ZGNRs为间接半导体.对于不同波矢状态,费米面附近价带上电子在原胞中各原子上的密度分布如图5(b),对于 kx=0的Γ点,PD-ZGNRs边界五边形环结构中3,4原子上电子密度较大,1,2原子上电子密度稍小,其他原子上电子密度为零;而对于波矢 kx=±0.5处,边界悬挂的19,20原子上的电子密度较大,其他原子上电子密度近似为零.此种结构的PD-ZGNRs的导电电子主要分布在边界畸变的五边形环的原子和边界悬挂的原子上,且两边界的导电性也不相同.
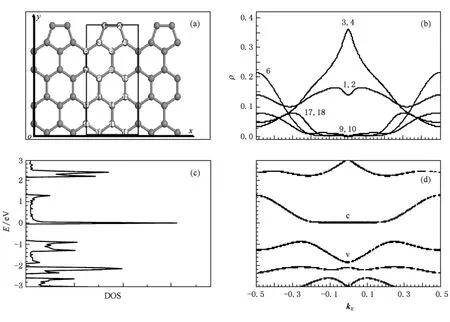
图3 PN-ZGNRs原胞中含18个原子的几何结构和电子结构 (a)PN-ZGNRs的几何结构示意图,其中虚线框表示原胞;(b)PN-ZGNRs费米面附近价带上电子在原胞中各原子上的密度分布;(c)PN-ZGNRs的电子态密度;(d)PN-ZGNRs的能带结构

图4 DD-ZGNRs原胞中含10个原子的几何结构和电子结构 (a)DD-ZGNRs的几何结构示意图,其中虚线框表示原胞;(b)DD-ZGNRs费米面附近价带上电子在原胞中各原子上的密度分布;(c)DD-ZGNRs的电子态密度;(d)DD-ZGNRs的能带结构
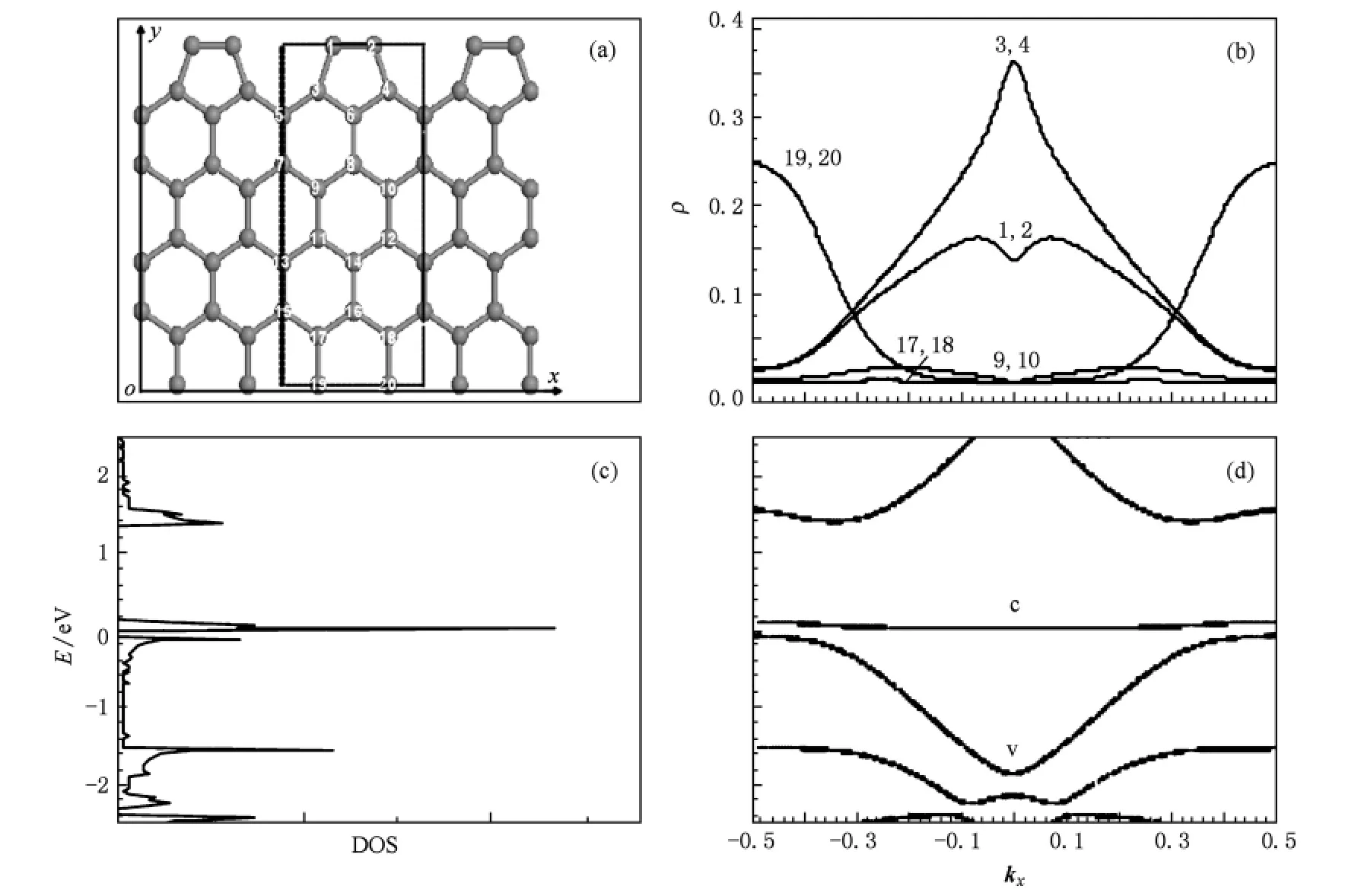
图5 PD-ZGNRs原胞中含20个原子的几何结构和电子结构 (a)PD-ZGNRs的几何结构示意图,其中虚线框表示原胞;(b)PD-ZGNRs费米面附近价带上电子在原胞中各原子上的密度分布;(c)PD-ZGNRs的电子态密度;(d)PD-ZGNRs的能带结构

图6 SPP-ZGNRs原胞含20个原子的几何结构和电子结构 (a)SPP-ZGNRs的几何结构示意图,其中虚线框表示原胞;(b)SPP-ZGNRs费米面附近价带上电子在原胞中各原子上的密度分布;(c)SPP-ZGNRs的电子态密度;(d)SPP-ZGNRs的能带结构
在DD-ZGNRs的结构基础上考虑1,2原子和19,20原子都成键,SPP-ZGNRs(以字母 S表示结构对称)结构如图6(a)所示,原胞内原子数N=20,晶格常数为其能带结构与态密度如图6(d),(c)所示,最低导带向下凹陷越过能量 E=0 eV在Γ点波矢kx=0和kx=±0.12处,与最高价带相交,且能带交叠度为1.01 eV,能隙Eg=0,费米能在E=-0.932 eV处,此种结构的SPP-ZGNRs显示为金属性质.对于不同波矢状态,费米面附近最高价带上电子在原胞中各原子上密度分布如图6(b)所示,对于kx=0的 Γ点,SPP-ZGNRs边界上对称的五边形环结构中3,4和17,18原子上电子密度较大,而1,2和19,20原子上电子密度稍小,其他原子上电子密度为零;而对于kx=±0.5时,五边形环中的6,16原子上电子密度较大.此种对称结构的SPP-ZGNRs的导电电子主要分布在边界对称的五边形环的原子上,因此发生畸变的边界部位的导电性比其他部位的导电性好.
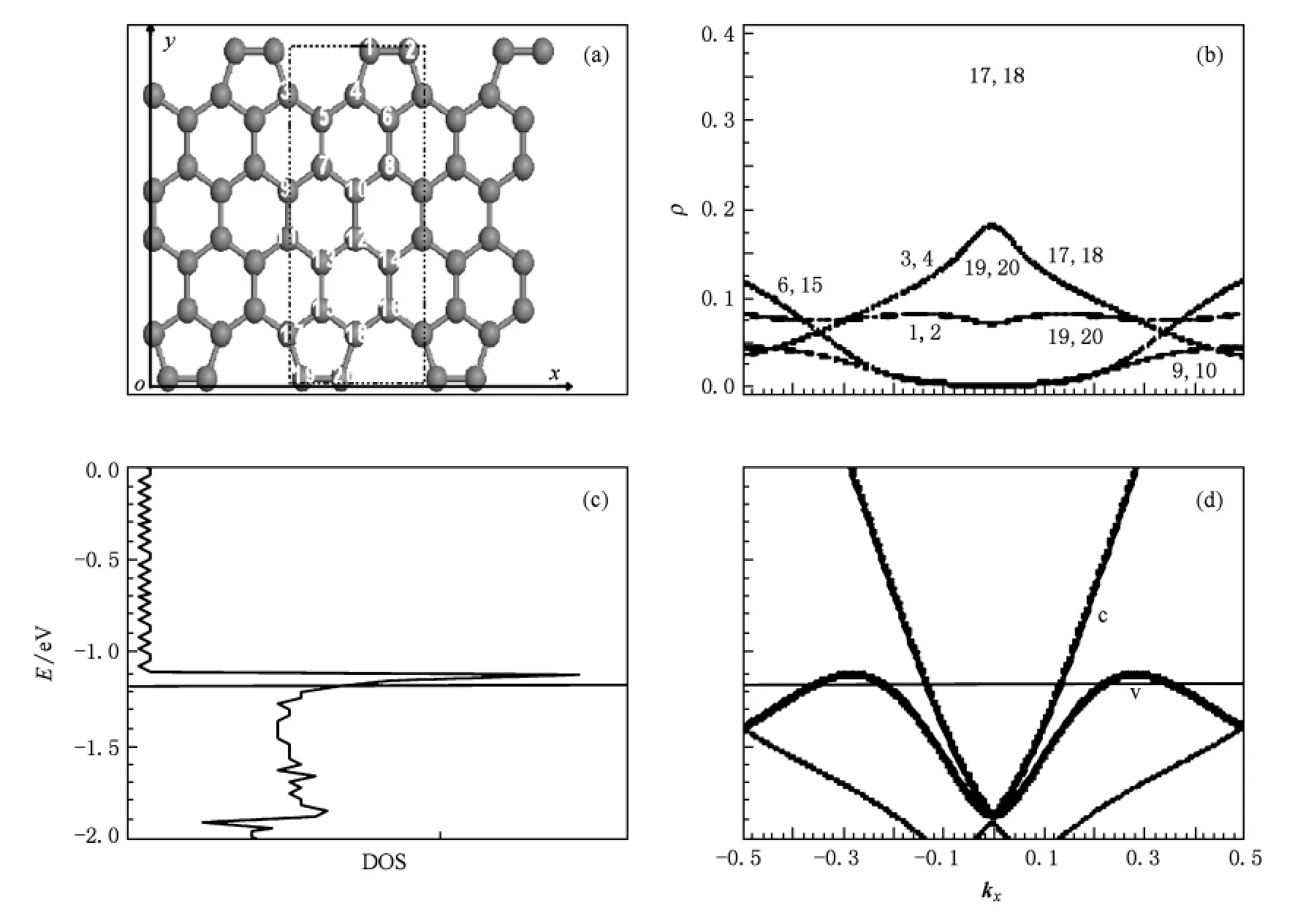
图7 ASPP-ZGNRs原胞中含20个原子的几何结构和电子结构 (a)ASPP-ZGNRs的几何结构示意图,其中虚线框表示原胞;(b)ASPP-ZGNRs费米面附近价带上电子在原胞中各原子上的密度分布;(c)ASPP-ZGNRs的电子态密度;(d)ASPPZGNRs的能带结构
继续在DD-ZGNRs的结构基础上考虑1,2原子和19,20原子都成键,但在两个边界相对的方向上交错成键,结构如图7(a)所示,用 ASPP-ZGNRs(字母AS表示结构不对称)表示.图7(a)中原胞内原子数N=20,晶格常数为.石墨烯能带结构和电子态密度如图7(d),(c)所示,最低导带向下凹陷越过能量E=0 eV处并与最高价带在Γ点波矢kx=0处相交,无能隙,且能带交叠度为0.77 eV,费米能在 E=-1.169 eV处,此种结构的 ASPPZGNRs显示为金属性.对于不同波矢状态,费米面附近最高价带上电子在原胞中各原子上的密度分布如图7(b)所示,对于kx=0的Γ点,ASPP-ZGNRs边界的五边形环结构中3,4和17,18原子上的电子密度较大,1,2和19,20原子上电子密度稍小于前者,其他原子上电子密度为零;对于 kx=±0.5处,ASPP-ZGNRs边界的五边形环中的6,15原子上的电子密度较大.此种结构的ASPP-ZGNRs的导电电子主要分布在边界不对称的五边形环的原子上,因此发生畸变部位的导电性比其它部位的导电性好.

图8 DN-ZGNRs与DD-ZGNRs(包括对称与不对称结构)的能隙与原子数的关系 结构如图2和4所示
下面我们用能隙随宽度的变化来分析石墨纳米烯的宽度对能带结构的影响.
以图2(a)的DN-ZGNRs结构为基础,在下边界处增加原子,ZGNRs的能隙与原胞中原子数的关系如图8所示.当原胞中原子数N为奇数时,只有一边界有原子悬挂为DN-ZGNRs结构,此时能隙为零;当原胞中原子数N为偶数时,两边界都有原子悬挂为DD-ZGNRs结构,能隙不为零,且每增加两个原子(半个周期),Eg变为原来值的1/2.能隙随宽度迅速衰减,当原子数增大到20时,Eg已趋于零.由此我们可以看出,对于宽度较大的 DD-ZGNRs和DNZGNRs都表现为金属性.

图9 PN-ZGNRs和PD-ZGNRs的能隙与原子数的关系 结构如图3和5所示
以图3(a)的PN-ZGNRs结构为基础,在下边界增加原子数时,ZGNRs的能隙与原胞中原子数的关系如图9所示.可以看到当原胞中原子数的一半N/2为奇数时,石墨烯为一边界原子成五边形环结构,另一边界无悬挂原子形成PN-ZGNRs结构,能隙稍大;当N/2为偶数时,石墨烯为一边界原子成五边形环结构,另一边界为悬挂原子,形成PD-ZGNRs结构,能隙相对于 PN-ZGNRs很小.随着原子数增多,PD-ZGNRs结构的能隙随原子数的增加而迅速减小,至40个原子数时近似为零;PN-ZGNRs结构的能隙随原子数的增加呈指数减小,最后趋于一个定值0.154 eV.
如果以图6(d)的 SPP-ZGNRs结构为基础,增加宽度,各能带图与图6(d)相似,导带向下凹陷越过能量E=0 eV处与价带在Γ点相交,能隙为零.如果两边交错成五边形环结构时,增加原子数,各能带与图7(d)类似,导带底与价带顶在Γ点相交,能隙为零.由此得到,PN-ZGNRs为半导体性,而PDZGNRs部分为能隙较小的半导体,原子数增加时转变为金属性,SPP-ZGNRs与 ASPP-ZGNRs都具有金属性.
4.结 论
本文运用紧束缚模型计算了七种不同边界的ZGNRs的能带结构及费米面附近价带上电子在原胞中各原子上的密度分布情况.计算发现 NNZGNRs,DN-ZGNRs,SPP-GNRs和 ASPP-GNRs为金属性;DD-ZGNRs,PD-GNRs和 PN-GNRs为半导体性,且能隙与宽度成反比.DD-ZGNRs和 PD-GNRs的能隙随宽度增加迅速减小至零.当原胞中原子数增加到20时,DD-GNRs转变为金属性;当原胞中原子数增加到40时,PD-GNRs转变为金属性.而 PNZGNRs的能隙随宽度增大呈指数减小至一有限值0.154 eV.计算还发现不同边界结构对费米面附近价带上电子分布产生的影响不同,并且在石墨烯边界原子上电子概率都相对较高.此外,我们还分别计算了这七种不同边界结构的ZGNRs的总能量,发现半导体性的PN-ZGNRs能量最低.说明此种结构相对其他几种结构更稳定,而且为半导体性.综上所述锯齿型石墨烯纳米带对于不同的边界结构可以是半导体性也可以是金属性,对于PN-ZGNRs总是半导体性的,这也正好能解释以往理论计算与实验结果相矛盾的原因在于石墨烯纳米带具有不同边界结构.
[1] Novoselov K S,Geim A K,Morozov S V,Jiang D,Zhang Y,Dubonos S V,Grigorieva I V,Firsov A A 2004 Science 306 666
[2] Katsnelson M I,Novoselov K S,Geim A K 2006 Nat.Phys.2 620
[3] Castro Neto A H,Guinea F,Peres N M R,Novoselov K S,Geim A K 2009 Rev.Mod.Phys.81 110
[4] Zhang Y B,Tan Y W,Stormer H L,Kim P 2005 Nature 438 201
[5] Nomura K,MacDonald A H 2006 Phys.Rev.Lett.96 256602
[6] Brey L,Fertig H A 2006 Phys.Rev.B 73 195408
[7] Westervelt R M 2008 Science 320 324
[8] Matulis A,Peeters F M 2008 Phys.Rev.B 77 115423
[9] Pedersen T G,Flindt C,Pedersen J,Mortensen N A,Jauho A P,Pedersen K 2008 Phys.Rev.Lett.100 136804
[10] Xu H Y,Heinzel T,Zozoulenko I V 2009 Phys.Rev.B 80 045308
[11] Sahu B,Min H,MacDonald A H,Banerjee1 S K 2008 Phys.Rev.B 78 045404
[12] Castro E V,Peres N M R,Lopes dos Santos J M B,Castro Neto A H,Guinea F 2008 Phys.Rev.Lett.100 026802
[13] Jin Z F,Tong G P,Jiang Y J 2009 Acta Phys.Sin.58 8537(in Chinese)[金子飞、童国平、蒋永进2009物理学报 58 8537]
[14] Wimmer M,Adagideli I,Berber S,Tomanek D,Richter K 2008 Phys.Rev.Lett.100 177207
[15] Yang L,Cohen M L,Louie S G 2007 Nano Lett.7 3112
[16] Son Y W,Cohen M L,Louie S G 2006 Phys Rev.Lett.97 216803
[17] Barone V,Hod O,Scuseria G E 2006 Nano Lett.6 2748
[18] Son Y W,Cohen M L,Louie S G 2006 Nature 444 347
[19] Brey L,Fertig H A 2006 Phys.Rev.B 73 235411
[20] Zhou B H,Duan Z G,Zhou B L,Zhou G H 2010 Chin.Phys.B 19 037204
[21] Rozhkov A V,Savel’ev S,Nori F 2009 Phys.Rev.B 79 125420
[22] Areshkin D A,Gunlycke D,White C T 2007 Nano Lett.7 204
[23] Ezawa M 2006 Phys.Rev.B 73 045432
[24] Han M Y, zyilmaz B,Zhang Y,Kim Philip 2007 Phys.Rev.Lett.98 206805
[25] Ouyang F P,Wang H Y,Li M J,Xiao J,Xu H 2008 Acta Phys.Sin.57 7132(in Chinese)[欧阳方平、王焕友、李明君、肖 金、徐 慧2008物理学报57 7132]
[26] Cresti A,Roche S 2009 Phys.Rev.B 79 233404
[27] Lee G D,Wang C Z,Yoon E,Hwang N M,Ho K M 2010 Phys.Rev.B 81 195419
[28] Li Z Z 2002 Solid State Theory(2nd ed)(Beijing:Higher Education Press)p67(in Chinese)[李正中 2002固体理论(第二版)(北京:高等教育出版社)第67页]
[29] Zheng X H,Dai Z X,Wang X L,Zeng Z 2009 Acta Phys.Sin.58 S259(in Chinese)[郑小宏、戴振翔、王贤龙、曾 雉2009物理学报58 S259]
Band structures of zigzag graphene nanoribbons*
Wang Xue-Mei Liu Hong
(Department of Physics and Science,Nanjing Normal University,Nanjing 210046,China)(Received 24 May 2010;revised manuscript received 7 July 2010)
Based on the π-electron tight-binding model,for zigzag graphene nanoribbons(ZGNRs)the influence of boundary structure on band structure,specially the electrons of the valence band and the conductor band near the Fermi level,are studied in detail.We investigate the band structures and the distributions of electrons of different atoms in a unit cell of the valence band near the Fermi level of ZGNRs with seven reasonable boundary structures.We find NN-ZGNRs with no dangling atoms on both edges,DN-ZGNRs with dangling atoms only on one edge,SPP-ZGNRs and ASPP-ZGNRs each with pentagons on both two edges and being metallic,DD-ZGNRs with dangling atoms on both two edges,PN-ZGNRs each with a defective structure of pentagons on one edge and no dangling atoms on the other edge,PD-ZGNRs with a pentagon on one edge and dangling atoms on the other edge being semiconducting,and the energy gap being inversely proportional to the width of nanoribbons.But for DD-ZGNRs and PD-ZGNRs,the energy gaps quickly reduce to zero with the increase of width;for PN-ZGNRs,the energy gaps decrease exponentially to a limited value of 0.154 eV.It is found that different boundary structures have different effects on the distribution of electrons in the valence band near the Fermi level.And the probability for electrons staying in the atoms on two edges of nanoribbons is relatively large.
zigzag graphen nanoribbons,tight-binding model,the distribution of electrons,the defective structure
.E-mail:liuhong3@njnu.edu.cn
*国家自然科学基金(批准号:10947004),江苏省自然科学基金(批准号:BK2008427),高校博士学科点专项基金(批准号:200803190004)资助的课题.
.E-mail:liuhong@njnu.edu.cn
*Project supported by the National Natural Science Foundation of China(Grant No.10947004),the Natural Science Foundation of Jiangsu Province in China(Grant No.BK2008427),the Doctoral program Foundation of Institution of High Education,China(Grant No.200803190004).
PACS:71.15.Ap,71.20.Tx

