用MRCI方法研究CS+同位素离子X2Σ+和A2Π态的光谱常数与分子常数*

刘 慧 邢 伟 施德恒† 朱遵略 孙金锋

1)(信阳师范学院物理电子工程学院，信阳 464000)

2)(河南师范大学物理与信息工程学院，新乡 453007)

1.引 言

在星际分子云中，已观测到许多含硫化合物，如 CS，CS+，HCS，HCS+，C2S及 C5S 等［1—4］. 其中CS+在电荷转移反应形成星际介质CS的过程中起重要作用［5］，其光谱特性已引起人们的广泛关注.在过去的几十年里，人们已对这一离子的各种光谱性质进行了大量的研究［5—25］.

实验方面，Jonathan 等［6］，King 等［7］和 Frost等［8］于1972年报告了该离子的真空远紫外光电子谱，进行了振动分析并得到了少量的光谱常数.1975年，List等［9］在观测 CS的光谱时指出，CS+离子在星际空间肯定存在.1976年，Coxon等［10］在研究He(23S)与 CS2的碰撞中观测到了 CS+离子的A2Π→X2Σ+跃迁，并获得了该离子 X2Σ+和 A2Π 态的某些光谱常数和若干低振动态的振动能级、经典转折点等分子常数.1977年，Gauyacu等［5］在600—800 nm内记录了CS+离子的发射谱并分析了A2Π→X2Σ+转动跃迁，得到了该离子 X2Σ+和 A2Π态的部分光谱常数和某些分子常数.1980年Tsuji等［12，13］在 220—340 nm 内观测并标识了该离子的B2Σ+→X2Σ+谱带、对其进行了振动分析并拟合出了部分光谱常数.1981年 Obase等［15］由 CS+的B2Σ+-A2Π 及 B2Σ+-X2Σ+谱线导出了 B2Σ+态 υ′=0—6 的振动分布.1993年 Cossart等［17］根据CS+离子 B2Σ+—X2Σ+和 B2Σ+- A2Π 的发射谱，拟合得到了少量的分子常数.1995年Coppens等［18］从对CS的光游离质谱分析中，得到了 CS+离子基态的离解能.2000—2002 年间，Liu等［20，21］利用激光吸收谱对 CS+离子的 A2Π←X2Σ+跃迁进行了详尽的研究，并拟合出了该离子 X2Σ+和 A2Π电子态的若干振动态的转动惯量、离心畸变常数及振动能级.综合已有的实验数据可以看出，仅有的实验研究都只涉及该CS+离子的部分光谱常数和较低振动态的分子常数;对于较高振动态的分子常数及12C34S+和12C33S+等同位素离子，实验暂未涉及.

理论方面，仅有 Larsson［22］，Midda 等［23］和Honjou［24，25］先后开展过类似的研究工作.1985 年Larsson［22］采用完全活性空间自洽场(CASSCF)及组态相互作用方法计算了该离子X2Σ+，A2Π和B2Σ+态的势能曲线并拟合出了各态的光谱常数;2003年，Midda等［23］采用密度泛函(HF/DF B3LYP)方法对该离子基态的键长、谐振频率等光谱常数等进行了探讨;2006年，Honjou［24］利用组态相互作用方法计算了 CS+前5个2Σ+态及前3个2Π 态的电子结构和能量，得到了相应的光谱常数.2008年Honjou［25］再 次 对该离子 的 X2Σ+，A2Π，B2Σ+及C2Σ+态进行研究，拟合出了各态的光谱常数及某些振动能级.显见，已有的理论计算［22—25］对 X2Σ+和A2Π态的Re与ωe研究较多，但其它光谱常数却涉及较少，且这些计算结果均偏离实验值较大，同时所有的理论计算都未涉及同位素识别.虽然也有理论［25］计算振动能级，但得到的结果却偏离实验值较大.鉴于这些原因，本文对该离子 X2Σ+和A2Π态的光谱常数及振动能级等分子常数进行了详尽的研究.

12C和13C的天然丰度大约是98.93% 和1.07%.14C是放射性元素，含量极低.S有4个稳定同位素32S，33S，34S和36S，天然丰度分别为95.02%，0.75%，4.21%和0.02%.本文仅研究丰度相对较大的3个同位素离子:12C32S+(丰度94.00%)、12C34S+(丰度4.16%)和12C33S+(丰度0.74%).

本文使用内收缩多参考组态相互作用(MRCI)方法［26，27］和价态范围内的最大相关一致基 aug-ccpV6Z［29—31］在 Molpro 程 序 包［28］中 计 算 CS+离 子X2Σ+和A2Π态的势能曲线.利用这些势能曲线并通过同位素质量识别，拟合出12C32S+，12C34S+和12C33S+等同位素离子的光谱常数.最后通过求解双原子分子径向核运动的Schrödinger方程，找到CS+(X2Σ+)及CS+(A2Π)离子的全部振动态.针对每一振动态，在同位素识别的基础上还计算了它们的经典转折点、转动惯量及离心畸变常数.这些计算结果均与已有的实验数据相符很好.

2.计算方法

MRCI方法是一种可靠的势能曲线计算方法［32，33］.在势能曲线的计算中 MRCI方法只使用Abelian点群.CS+离子属于线性双原子分子离子，具有C∞υ对称性，因此在计算中只能由其子群 C2υ替代.C2υ子群共有4种类型的分子轨道，相对应的不可约表示是a1/b1/b2/a2.具体到含有21个电子的CS+离子，分析指出它默认参与运算的分子轨道有14个，分别是8个 a1，3个 b1和3个 b2轨道.其中，8个属于开壳层轨道(4a1，2b1和2b2)，分别对应于C原子的2s2p和S原子的3s3p轨道;6个属于闭壳层轨道，分别是4a1，1b1和1b2.

我们发现，当只采用这14个分子轨道(8a1，3b1，3b2)进行计算时，所得这两个态的势能曲线都不光滑.原因是一个态的势能曲线与另一个态有交叉.以A2Π态为例，当核间距约0.40 nm时，势能曲线出现跳变(由一个态跳到另一个态).这提示我们，为得到光滑的势能曲线，需要将更多的轨道放入活化空间.计算发现，当将1个额外的a1轨道、1个额外的b2轨道放入活化空间时(此时参与计算的分子轨道共16个，分别是9a1，3b1和4b2)，所得这两个态的势能曲线是光滑的.

MRCI计算以 CASSCF 波函数［34，35］为参考波函数.为得到满意的结果，这里C和S均使用价态范围内的最大相关一致基.即 C原子是(16s，10p，5d，4f，3g，2h，1i)/［7s，6p，5d，4f，3g，2h，1i］，S 原子是(21s，14p，5d，4f，3g，2h，1i)/［8s，7p，5d，4f，3g，2h，1i］，均记为 aug-cc-pV6Z.

为准确计算该离子X2Σ+和A2Π态的离解能，本文首先在MRCI/aug-cc-pV6Z理论水平下对其进行几何优化，以便在进行势能曲线计算时，平衡位置能准确地成为势能曲线的一个计算点.当核间距达到0.60 nm左右时，这两个态的势能值都保持为一个常数而不随核间距的增大而发生变化，因此势能曲线的计算范围可取为0.05—0.60 nm.计算过程中，步长一般取0.05 nm，只是在平衡位置附近为清晰展现这两个态的细节特性，计算步长才取为0.02 nm.扫描得到的这两个态的势能曲线都是完全收敛的.

计算中，我们也在一个较小的核间距范围内考虑了相对论效应及核价相关效应对光谱常数计算结果的影响.我们发现，这两种修正对光谱常数的影响都很小.考虑到在一个较大的核间距范围内进行这两种修正需要耗费大量机时，而且价态范围内的计算结果已经能很好地反映该离子的光谱特性，因此本文所述的计算仅在价态范围内进行.

利用Molcas程序包［36］拟合上述势能曲线并进行同位素识别，即可得到CS+各种同位素离子的光谱常数和分子常数.其中12C32S+，12C34S+和12C33S+的光谱常数列于表1中，12C32S+的分子常数则分别列于表2—5中.由于篇幅限制，表2—5只列出了前30个振动态的振动能级G(υ)、转动惯量Bυ及离心畸变常数Dυ.需要说明地是，由于12C32S+在CS+的各种同位素离子中所占的份额高达94%，因此对于那些未进行同位素识别的理论或实验结果，本文中都将其归类于12C32S+.

另外，本文还将这两个电子态的前30个振动态的经典转折点列于表2和表4中，以便于分析和比较.

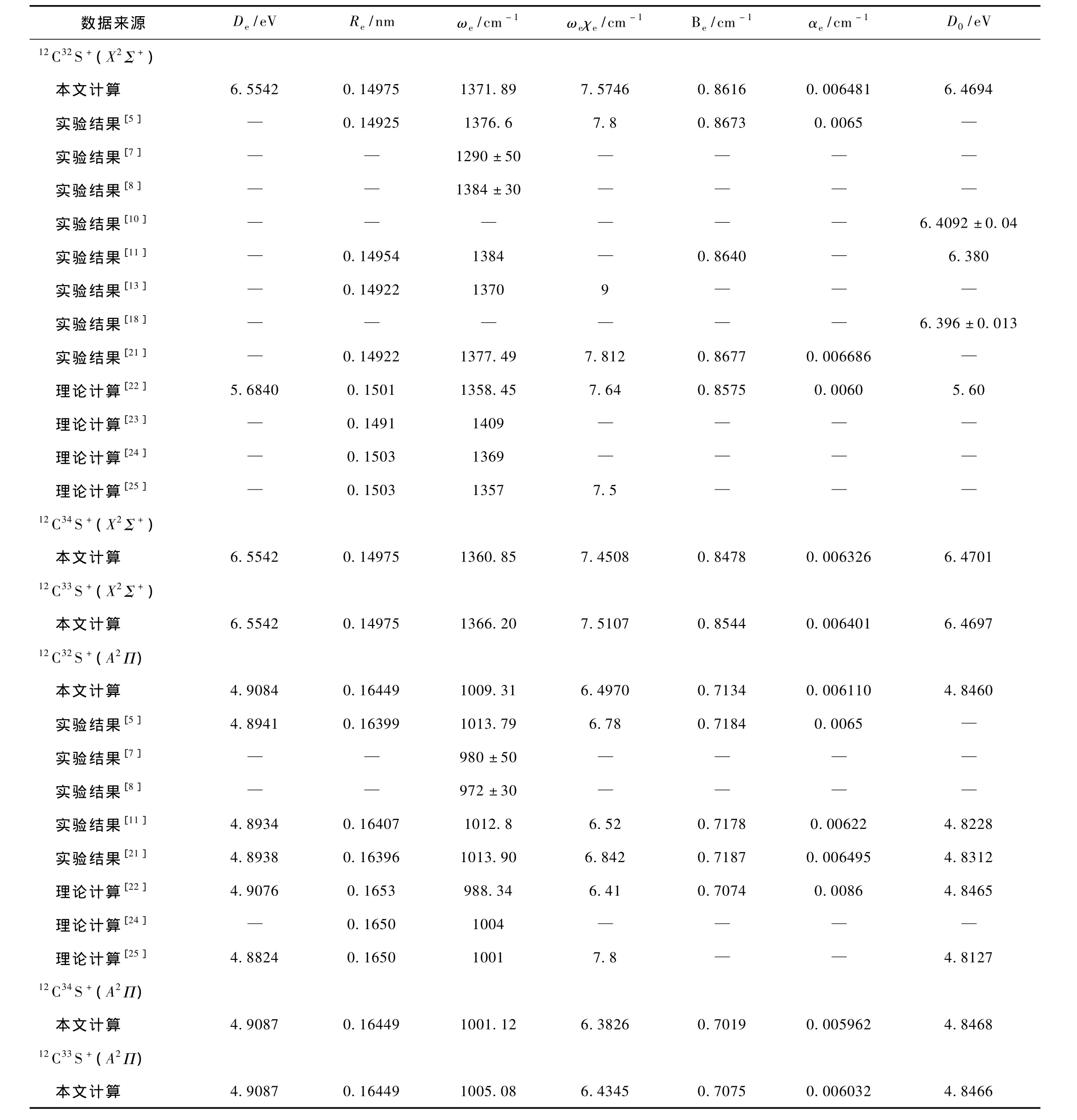
表1 MRCI/aug-cc-pV6Z理论水平下CS+各种同位素离子X2Σ+和A2Π态的光谱常数及与实验结果和其他理论结果的比较

3.结果与讨论

3.1.光谱常数

为便于比较，表1还列出了已有的实验结果［5，7，8，10，11，13，18，21］及其他理论结果［22—25］. 在这些计算结果中，较早的工作是由 Larsson［22］于1985年报道的.Larsson［22］采用CASSCF和组态相互作用方法在一个较小的核间距范围内计算了该离子X2Σ+，A2Π 和 B2Σ+态的势能曲线.计算中，C原子使用［14s，l0p，4d］/(8s，6p，4d)高斯收缩基;S原子使用［10s，6p］/(5s，4p)Dunning-Huzinaga基.利用得到的势能曲线，Larsson［22］拟合出了这些态的部分光谱常数.与实验结果［18］比较后发现，对于X1Σ+态，Larsson［22］的 D0值偏离该实验值［18］竟高达12.45%.谐振频率偏离实验结果［21］虽较小，但也有1.38%.对 A2Π 态来说，其 ωe比实验值［21］低了近26 cm-1，误差达2.52%.由于该态的离解能仅是在计算一小段势能曲线的基础上拟合得到的，因此其可靠性并不高.

2003年，Midda等［23］采用密度泛函(HF/DF B3LYP)方法和四个基组(从 6-311++G(2df，2pd)，6-311++G(3df，3pd)，cc-pVTZ，aug-ccpVTZ)对若干双原子分子及其离子的光谱性质进行了研究.关于CS+，他们计算了其基态的平衡核间距和谐振频率.与实验结果［21］比较后发现，当使用最大基组aug-cc-pVTZ时，他们得到的平衡核间距与这一实验值仅相差0.0001 nm.不过我们发现，虽然 Midda等［23］的 Re很准确，但其 ωe却比实验值［21］高2.3%.更重要地，他们没有计算该离子的其他光谱常数(如 De，ωeχe，αe和 Be等)，因而其结果存在很大的局限性.

2006 年，Honjou［24］用 MRCI方法在一个较小的核间距范围内计算了该离子前5个2Σ+态及前3个2Π态的势能曲线.通过拟合，他们得到了相应于各态的光谱常数(Te，Re和ωe).计算中，C和S均使用高斯型基函数.与实验结果［21］比较后发现，Honjou［24］得到的 Re和 ωe较为准确. 例如对于X1Σ+态，其 Re值只偏离这一实验结果［21］0.72%;ωe偏离这一实验结果［21］也只有0.62%;对 A2Π 态来说，Re值偏离这一实验结果［21］只有0.63%;ωe偏离这一实验结果［21］也只有0.98%，等等.但遗憾地是，Honjou［24］没有对该离子的其它重要光谱常数(如 De，ωeχe等)进行研究.最近，Honjou［25］用SOCI方法在一个较小的核间距范围内再次对该离子 X2Σ+，A2Π，B2Σ+及 C2Σ+态的势能曲线进行了计算，也获得了各态的光谱常数 Te，Re，ωe及ωeχe..通过比较我们发现，对于 X1Σ+和 A2Π 态，其Re值没有变化;但其 ωe偏离实验结果［21］的却明显加剧，因而对于光谱常数来说，文献［25］的计算质量未得到改善.

对于12C32S+(X2Σ+)，一方面，本文得到的平衡核间距Re及谐振频率 ωe与实验值［21］间的偏差只有 0.00053 nm和 5.6 cm-1，相对误差仅为0.36%和0.41%，显然优于文献［22，24，25］的计算结果.虽然文献［23］得到的 Re与实验结果［21］的偏差小于本文，但其 ωe值却偏离实验值［21］较大，且没有计算其他光谱常数;另一方面，本文的Be与实验值［21］间的相对误差也只有0.70%，显然优于文献［22］的计算结果.尽管本文的 αe与实验值［21］相比低了0.000205 cm-1，但与仅有的理论值［22］相比，本文结果有明显改善.至于D0值，本文的结果与实验值［10］间的偏差为0.94%，也大大优于文献［22］的计算结果.

对于12C32S+(A2Π)，一方面本文得到的 Re及ωe偏离实验值［21］分别只有0.32%和0.45%，这优于文献［22，24，25］的计算结果;另一方面，本文的 Be，αe及 ωeχe也与实验结果［21］符合很好，优于文献［22］得到的理论值.

据此以上分析可以得出结论:对于12C32S+(X1Σ+)及12C32S+(A2Π)，本文的光谱计算结果与实验值相当一致，并在总体上明显优于已有的理论值.这些都说明本文所采用的计算方法是可靠的，得到的光谱常数是准确、可信的.

遗憾地是，由于暂时还没有同位素离子12C34S+和12C33S+的实验或理论光谱常数，这里无法进行直接的数据比较.但前文的讨论和后文的分析结果都告诉我们，本文得到的势能曲线是准确、可靠的.由于本文使用的拟合方法［37—40］十分可靠，因此我们有理由相信表1列出的同位素离子12C34S+和12C33S+在这两个态的光谱常数也是可信的.

3.2.分子常数

利用本文得到的势能曲线，通过求解核运动的径向薛定谔方程，找到了 J=0时 CS+(X2Σ+)的全部68个振动态及 CS+(A2Π)的全部80个振动态.在 Molcas程序包［36］中，通过同位素质量识别还计算了每一振动态的振动能级、转动惯量及离心畸变常数等，并将计算结果分别列入表2—5中.为便于比较，表2—5也列出了已有的实验结果［5，16，17，20，21］及其他理论计算结果［25］.

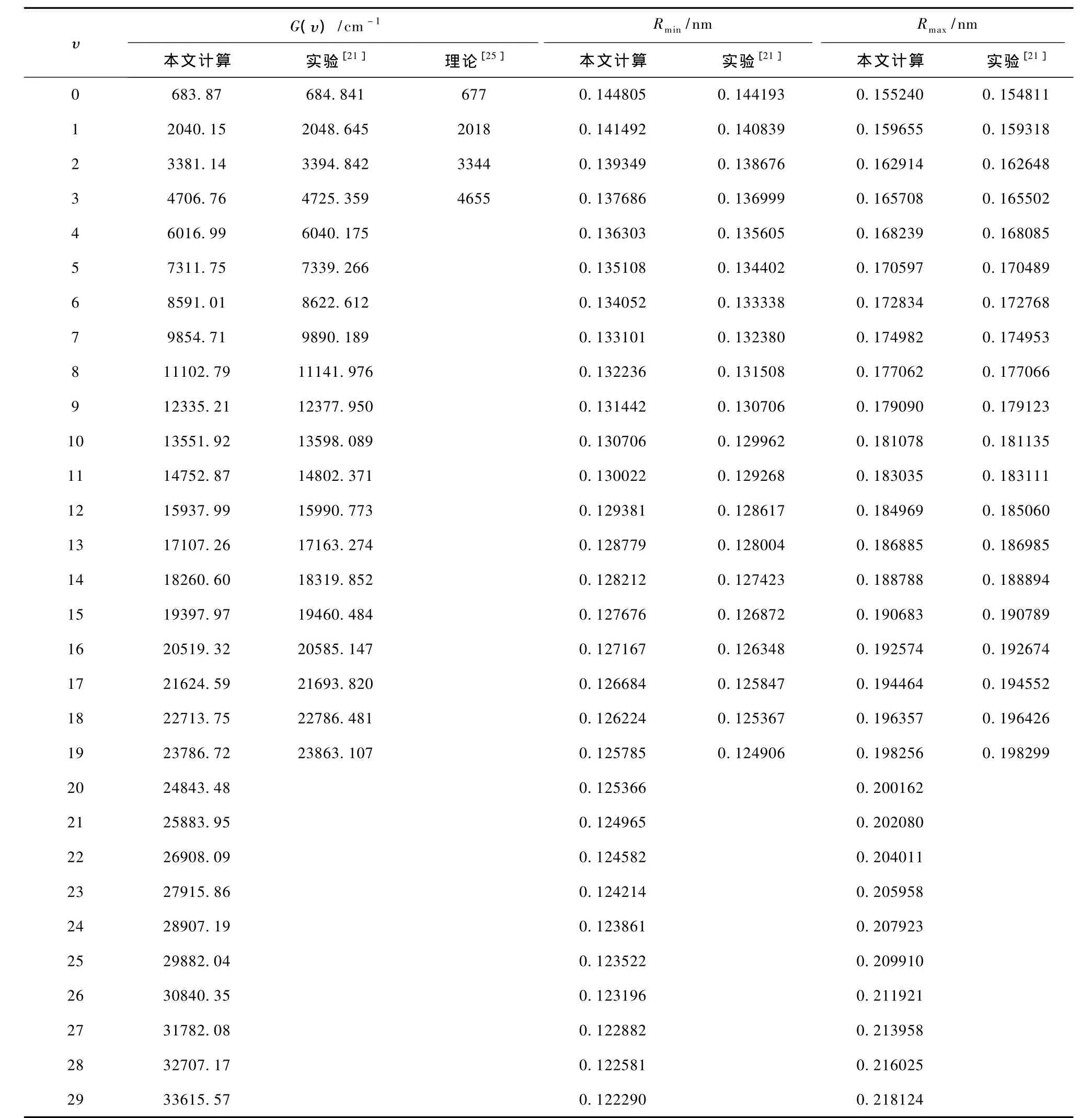
表2 MRCI/aug-cc-pV6Z理论水平下12C32S+(X2Σ+)的振动能级和经典转折点(J=0时)及与实验结果和其他理论结果的比较

只有一组实验［21］报道了该离子 X2Σ+态的振动能级与经典转折点(Rmin和 Rmax)，也只有一组理论［25］涉及该态振动能级的计算.一方面，从表2不难发现，本文得到的振动能级与实验值［21］的最大偏离不超过 0.40%，而 Honjou［25］的理论值与实验值［21］的最小偏离也有1.15%，因此本文的振动能级比仅有的理论计算结果［25］更加接近实验值［21］;另一方面，经典转折点也与仅有的一组实验结果［21］相当一致(Rmin和Rmax与该组实验数据的最大偏离也分别只有0.70%和0.28%)，都是十分准确的.

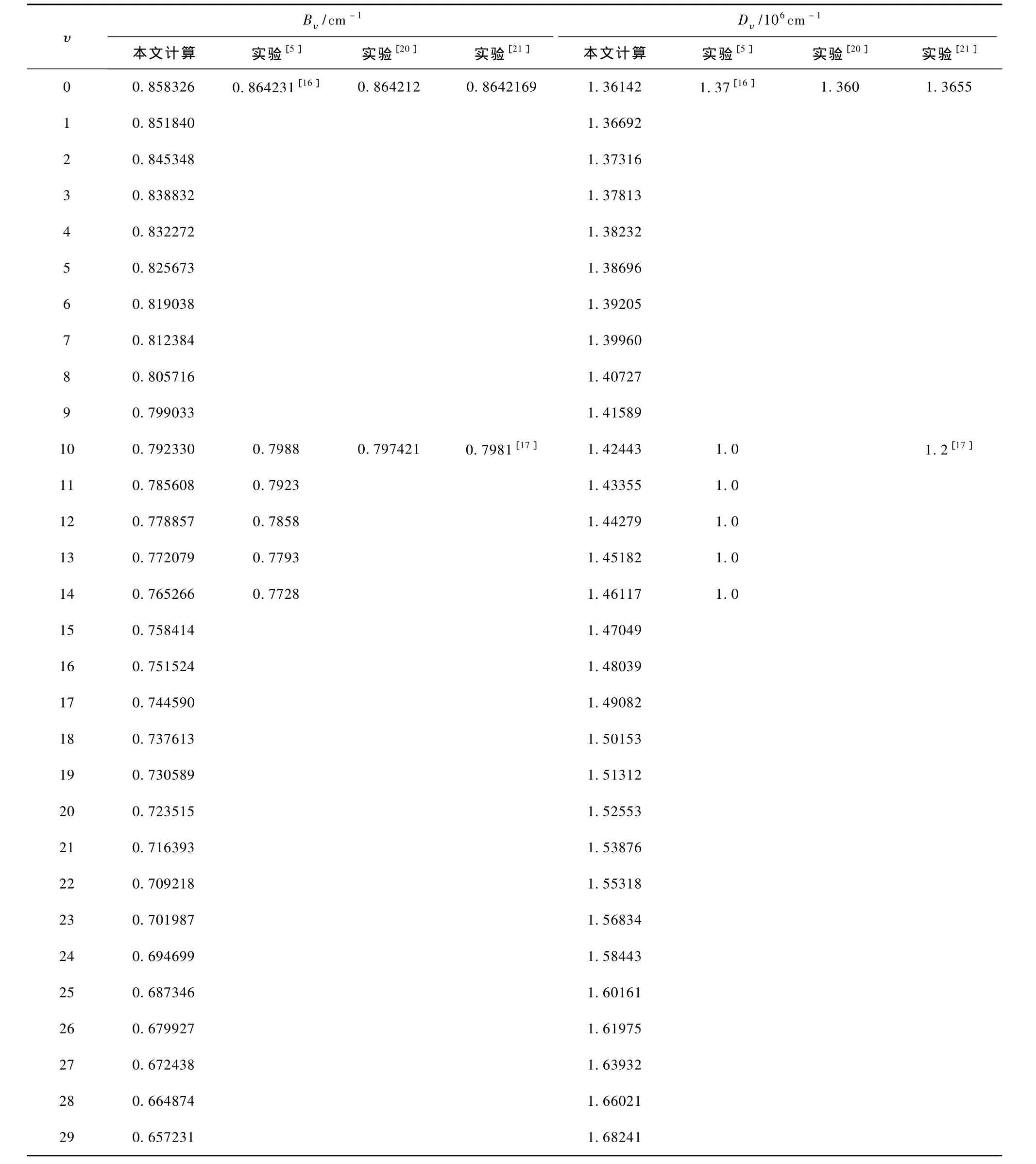
表3 MRCI/aug-cc-pV6Z理论水平下12C32S+(X2Σ+)的转动惯量和离心畸变常数(J=0)及与实验结果的比较

表3列出了本文得到的12C32S+(X2Σ+)离子的转动惯量 Bυ、离心畸变常数 Dυ及相应的实验结果［5，16，17，20，21］. 与这些实验结果相比，Bυ的最大偏差 分 别 只 有 0.97%［5］，0.68%［16］，0.72%［17］，0.68%［20］和 0.68%［21］，是非常准确的. 这里需要说明的是，实验［5］给出的Bυ值是在固定 Dυ值的基础上拟合得到的.因此实验［5］中的 Dυ值不具有可比性.

表4 MRCI/aug-cc-pV6Z理论水平下12C32S+(A2Π)的振动能级和经典转折点(J=0)及与实验结果和其它理论结果的比较

关于12C32S+(A2Π)，表4列出了本文得到的振动能级G(υ)、经典转折点(Rmin和Rmax)及已有的实验结 果［10，21］和 理 论 计 算 结 果［25］. 一 方 面， 与Honjou［25］的计算结果相比，除个别数据点外，本文的振动能级均更加接近实验值［10，21］.例如当υ=0时，虽然与实验［10］相比本文结果与理论结果［25］有相当的精度，但与文献［21］的实验相比本文的计算结果只略低0.32%，而文献［25］则偏低0.9%.当υ=8时与文献［21］的实验相比较，本文结果只偏离0.93%，而文献［25］则达到 1.64%;与文献［10］的实验相比较，本文结果偏离0.99%，而文献［25］则达到1.69%.另一方面，本文计算所得的经典转折点也与实验值［10，21］相当一致.详细的分析结果还表明，本文的Rmin和Rmax偏离实验结果［21］的最大值分别只有0.61%和0.24%，这些都是相当令人满意的.

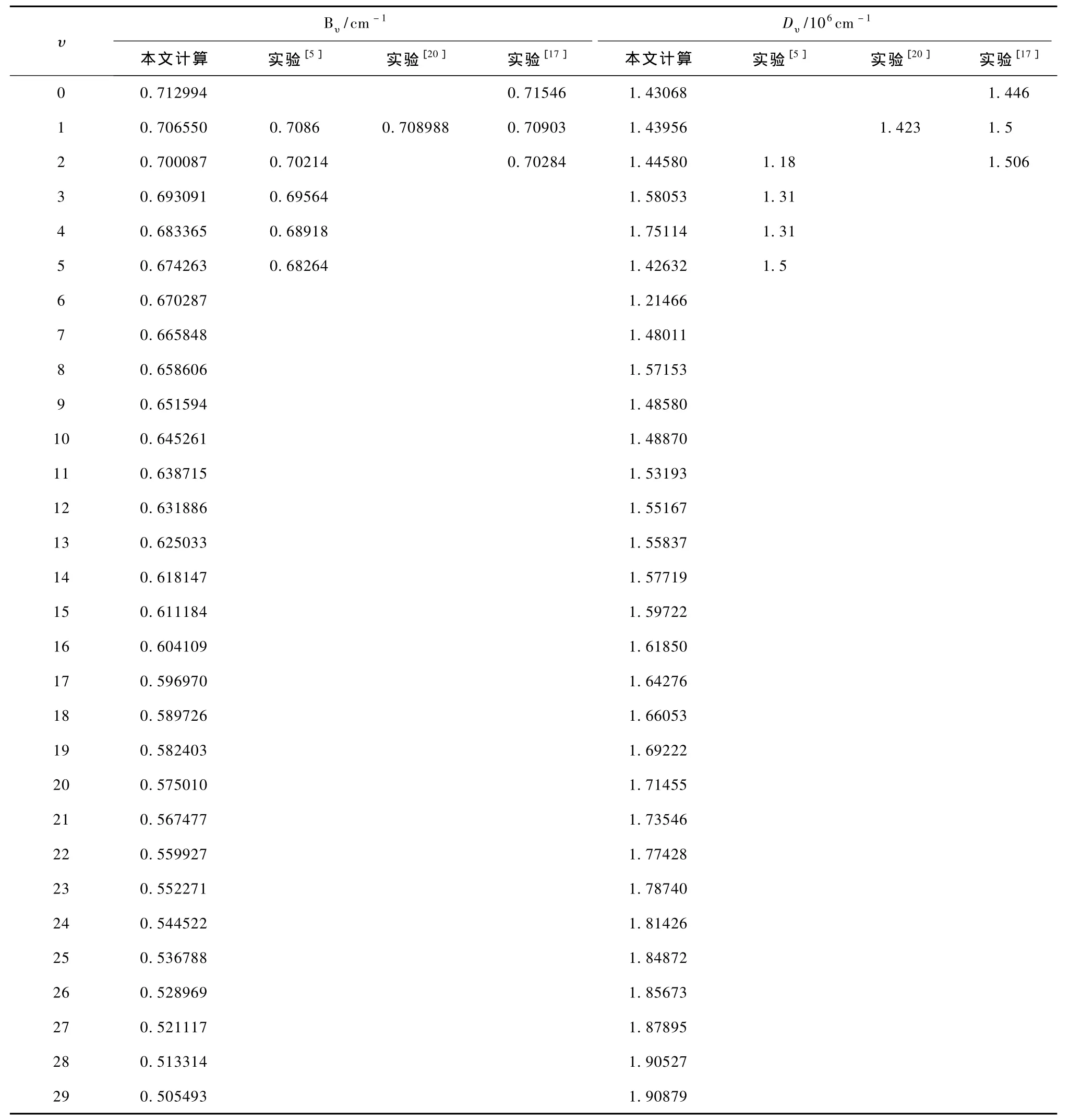
表5 MRCI/aug-cc-pV6Z理论水平下12C32S+(A2Π)的转动惯量及离心畸变常数(J=0)及与实验结果的比较

表5列出了12C32S+离子A2Π态的转动惯量、离心畸变常数及其相关实验结果［5，17，20］. 先分析 Bυ偏离实验结果的情况.与实验结果［17］相比，本文结果与其偏差最大不到0.40%，是非常好的;与实验结果［5］相比，本文值与其偏差最大也只有1.23%(这对应于υ=5的情况.除该点外，其余各点的最大偏差都不超过0.85%).另外，本文的计算结果与实验报道的仅有的实验值［20］也仅偏差0.34%.据此可以得出结论:本文得到的A2Π态的转动惯量是准确、可靠的.至于高阶小量Dυ，从表5也不难看出，本文的计算结果与实验值也很符合.

对于较高的振动态，文献中没有相关的实验数据及理论计算结果报道.但根据前面关于较低振动态的计算结果与实验结果及其他理论计算结果的比较与分析，我们足以相信，本文关于较高振动态的分子常数计算结果是准确、可靠的.本文关于较高振动态的计算结果可为进一步的实验研究提供可靠的数据参考.

4.结 论

本文利用精度较高的MRCI方法和价态范围内的最大相关一致基aug-cc-pV6Z，在0.05—0.60 nm的核间距范围内计算了 CS+(X2Σ+)和 CS+(A2Π)的势能曲线.利用得到的势能曲线并通过同位素质量标识，拟合得到了这两个态3种主要同位素分子离子的光谱常数 D0，De，Re，ωe，ωeχe，αe和 Be.本文的计算结果与已有的实验值均符合很好.利用本文得到的势能曲线，通过求解核运动的径向薛定谔方程，找到了 J=0时 CS+(X2Σ+)和 CS+(A2Π)的全部振动态，在同位素质量识别的基础上分别计算了每一振动态的振动能级、经典转折点、转动惯量及离心畸变常数等分子常数，所得结果也与实验数据一致.本文中，CS+离子两个电子态的同位素光谱常数和高振动态的分子常数系首次报道.

［1］Penzias A A，Solomon P M，Wilson R W，Jefferts K H 1971 Astrophys.J.，Lett.Ed.168 L53

［2］Thaddeus P，Guelin M，Linke R A 1981 Astrophys.J.Lett.，Ed.246 L41

［3］Saito S，Kawaguchi K，Yamamoto S，Ohishi M，Suzuki H，Kaifu N 1987 Astrophys.J.，Lett.Ed.317 L115

［4］Bell M B，Avery L W，Feldman P A 1993 Astrophys.J.Lett.417 L37

［5］Gauyacq D，Horani M 1978 Can.J.Phys.56 587

［6］Jonathan N，Morris A，Okuda M，Smith D J，Ross K J 1972 Chem.Phys.Lett.13 334

［7］King G H，Kroto H W，Suffolk R J 1972 Chem.Phys.Lett.13 457

［8］Frost D C，Lee S T，McDowell C A 1972 Chem.Phys.Lett.17 153

［9］List H S，Linke R A 1975 Astrophys.J.196 709

［10］Coxon J A，Marcoux P J，Setser D W 1976 Chem.Phys.17 403

［11］Huber K P，Herzberg G 1979 Molecular Spectra and Molecular Structure.(Vol.4)Constants of Diatomic Molecules(New York:Van Nostrand Reinhold Company)p184

［12］Tsuji M，Obase H，Nishimura Y 1980 J.Chem.Phys.73 2575

［13］Tsuji M，Obase H，Matsuo M，Endoh M，Nishimura Y 1980 Chem.Phys.50 195

［14］Erman P，Larsson M 1981 Physica Scripta 23 1052

［15］Obase H，Tsuji M，Nishimura Y 1981 Chem.Phys.57 89

［16］Horani M，Vervloet M 1992 Astron.Astrophys.256 683

［17］Cossart D，Horani M，Vervloet M 1993 Am.Inst.Phys.Conf.Proc.312 367

［18］Coppens P，Drowart J 1995 Chem.Phys.Lett.243 108

［19］Turner B E 1996 Astrophys.J.468 694

［20］Liu Y，Liu H，Gao H，Duan C，Hamilton P A，Davies P B 2000 Chem.Phys.Lett.317 181

［21］Liu Y，Duan C，Liu J，Wu L，Xu C，Chen Y，Hamilton P A，Davies P B 2002 J.Chem.Phys.116 9768

［22］Larsson M 1985 Chem.Phys.Lett.117 331

［23］Midda S，Das A K 2003 Eur.Phys.J.D 27 109

［24］Honjou N 2006 Chem.Phys.324 413

［25］Honjou N 2008 Chem.Phys.344 128

［26］Werner H J，Knowles P J 1988 J.Chem.Phys.89 5803

［27］Knowles P J，Werner H J 1988 Chem.Phys.Lett.145 514

［28］Werner H J，Knowles P J，Lindh R，Manby F R，Schütz M，Celani P，Korona T，Mitrushenkov A，Rauhut G，Adler T B，Amos R D，Bernhardsson A，Berning A，Cooper D L，Deegan M J O，Dobbyn A J，Eckert F，Goll E，Hampel C，Hetzer G，Hrenar T，Knizia G，K?ppl C，Liu Y，Lloyd A W，Mata R A，May A J，McNicholas S J，Meyer W，Mura M E，Nicklass A，Palmieri P，Pflüger K，Pitzer R，Reiher M，Schumann U，Stoll H，Stone A J，Tarroni R，Thorsteinsson T，Wang M，Wolf A 2008 Molpro，version 2008.1，a package of ab initio programs

［29］Peterson K A，Kendall R A，Dunning T H 1993 J.Chem.Phys.99 1930

［30］Woon D E，Dunning T H 1993 J.Chem.Phys.99 1914

［31］Dunning T H 1989 J.Chem.Phys.90 1007

［32］Wang X Q，Yang C L，Su T，Wang M S 2009 Acta Phys.Sin.58 6873(in Chinese)［王新强、杨传路、苏 涛、王美山 2009物理学报58 6837］

［33］Bai F J，Yang C L，Qian Q，Zhang L 2009 Chin.Phys.B 18 549

［34］Werner H J，Knowles P J 1985 J.Chem.Phys.82 5053

［35］Knowles P J，Werner H J 1985 Chem.Phys.Lett.115 259

［36］Krogh J W，Lindh R，Malmqvist P°A，Roos B O，Veryazov V，Widmark P O 2009 User Manual，Molcas Version 7.4(Lund:Lund University)

［37］Shi D H，Zhang X N，Sun J F，Zhu Z L 2010 Chin.Phys.B 19 013501

［38］Shi D H，Zhang J P，Sun J F，Liu Y F，Zhu Z L 2009 Acta Phys.Sin.58 5329(in Chinese)［施德恒、张金平、孙金峰、刘玉芳、朱遵略 2009物理学报 58 5329］

［39］Zhang X N，Shi D H，Zhang J P，Zhu Z L，Sun J F 2010 Chin.Phys.B 19 053401

［40］Shi D H，Zhang J P，Sun J F，Liu Y F，Zhu Z L 2009 Acta Phys.Sin.58 7646(in Chinese)［施德恒、张金平、孙金峰、刘玉芳、朱遵略 2009物理学报 58 7646］