数学解题思维与解法发现的途径

广 东 叶国强

数学解题思维与解法发现的途径

广 东 叶国强

掌握思考方法是学习数学的重要环节，本文围绕数学常用思考方法展开论证，揭示解题规律。

解题途径；细分；变换；试猜；逼近

苏联教育家加里宁说过：“数学是思维的体操。”这确实至理名言。学好数学，能使思维敏捷、清晰、精细。数学的训练价值在何处，其思维规律是什么？不少人的做法是“大量运动”训练，认为做题千万，奥妙自得，无须问什么规律。这当然谈不上科学性，“熟读唐诗三百首，不会作诗也会吟”，乃是找不到“规律性”时不得已而为之，时至今日，似乎已到了大力研究数学思维规律，科学地设计“思维体操”的时候了。下面就数学解题的思维过程及解法发现的途径进行探讨。

解题思维过程究竟是什么样才最为合适？许许多多人都在思考与研究这个问题。苏联著名的数学家C.A亚诺夫斯卡娅对“解题是什么”的回答惊人的简单：“解题就是把习题归结为已经解过的问题”，就是说，要努力把非基本题分解成或归结为基本题。苏联心理学家鲁宾斯坦认为，“人们解题是一个改编习题的过程”。在这个过程中，通过综合习题条件和要求之间的联系，对这些条件和要求进行不断的分析、综合与概括的过程。世界著名的数学家波利亚指出，要构想出一个解题计划的思路，经常有用的办法是：不断地变换你的问题，“试验对问题作各种修改。我们必须一再地变化它……直到最后成功……”。解决数学问题的思维过程，可以认为就是不断变换问题的过程，从而也是一种试错的过程。

下面就以“细分”、变换”、“试、猜”、“逼近”为纲，具体分析数学解题法发现的一般途径。

一、化解与叠加

“化整为零”，“化大问题为小问题”，“分而治之”，历来是各方明智之士解决困难的诀窍之一，也是我们在数学解题中经常使用的一种思想方法。

具体地把一个数学问题分解开来的方法，又有两大类型：一是把一个较困难的问题，分解成一组系列题，这组题目中，前一个题的结果往往直接影响到后一个题的解答：通常是后一个题的一个或几个已知条件；二是把一个大问题，分割成有并列关系的几个题，这几个题目之间，在解决方法上可能会有某种相似或联系，但没有前一个题的结果，后一个题一般仍然可以独立地予以解答。前者的关键是发现几个解题理论中的所谓中途点；后者的要津，是找到一个或几个比较容易处理的所谓导引特款（波利亚）。

（一）中途点与纵向分解

其意义和实质在于：通过纵向地“分解大问题为小问题”，用两个或多个较简单的问题“串联”来代替一个难题。找到有希望恰好落在通向“终点”的道路上的中途点，能大大地缩小解题的尝试范围。

（二）导引特款与横向分解

所谓导引特款，通常指的是对于待解决的问题，可以起导引作用的某特殊情形。波利亚认为，“从一个或几个导引特款出发，利用特殊情形的叠加去得出一般问题的解”，是数学解题中的一个有用模式。叠加，这里是把各种特殊情形采用适宜的方式组合起来的意思。教科书上圆周角定理的证明是这个模式的一个典型例子。

二、等价与映射

一个数学问题，往往具有种种不同的表达形式，相应地也有种种不同的处理方法。由于这些处理方法的难易程度各不同，这样，这些表达形式的难易就会因人而异。因此，要解决一个问题，对不同的人，就在于选择一种恰当的表达形式，以便利用他自己所熟悉的工具。从这种观点来看，把一个问题变换成种种等价形式，或映射到另一个领域中去，势必将大大地增加这个问题的可能性。下面举一些例子加以说明。

1.命题的等价变换。找到命题的等价条件，通过恒等变换是常用的手法。

三、试探与猜想

伟大的数学家、教育家波利亚在《数学与猜想》一书中指出：“数学家的创造性工作成果是论证推理，既证明；但是这个证明是通过合情推理，通过猜想而发现的，只要数学的学习过程稍能反映出数学的发明过程的话，那么就应当让猜测、合情推理占有适当的位置”。他强调教学必须为发明作准备，或至少给一点发明的尝试，他向教授呼吁"让我们猜想吧！"这是应该引起我们重视的问题。在数学教学中适当反映数学的发现过程，培养学生直觉思维，学会通过合情推理，提出猜想，这是现代数学教育工作中的重要任务。

1.观察发现

许多数的性质，是由观察发现的，著名的哥德巴赫猜想，就是在观察3+7=10,3+17=20,13+17=30后发现这三个式子都是两个奇素数之和为偶数，进而在观察最小的两个奇素数之和3+3=6，再观察超过6的偶数8=3+5,10=3+7=5+5,12=5+7,14=3+11=7+7，……从而提出大于4的偶数都是两个奇素数之和的猜想。可见观察是发现问题的第一步，观察力是发现能力的基础。在数学教学中我们赢尽可能给学生以观察发现的机会，如讲异面直线时，可以让学生观察所在教室的墙的交线的位置关系，在讲用祖衡原理求证球的体积之前，让学生观察实验，将半球装满水或砂子，倒入等低同高的圆柱体内，让学生发现圆柱体内水面高度，恰好是圆柱体内的高的，在观察的基础上，猜想两个半球体积是圆柱体积，即然后再证明。

2.合情推理的训练

合情推理的方法是多方面的，没有固定的标准。常用的有归纳法，类比法，特殊化和一般化的方法。

（1）归纳推理

归纳法是对某些单个的、特殊的食物进行分析比较，从中归纳出共同特征和规律，提出猜想，发现解决问题的方法，发现新的知识。归纳推理在数学的起源和发展中都起了重要作用，如微积分的建立是牛顿和莱姆尼茨将十七世纪以来许多数学家研究的成果，如求变化率的速率，抛线的切线，极值问题归纳为微分，而把处理从加速度求距离，求曲线长等归纳为反微分问题，这是归纳发现的例子。在数学史上提出猜想再证明的例子屡见不鲜。

为了培养学生归纳发现的能力，在数学中应尽可能让学生进行归纳发现活动。例如在学习一元二次方程根与系数的关系时，可让学生解几个具体的方程。如

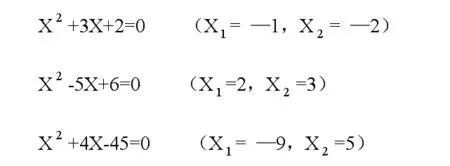
引导学生在观察基础上归纳发现根与系数关系。再如再解一些比较抽象的问题的时候，可以从具体例子开始研究运用归纳推理，寻求一般解法。在教学生归纳方法的时候，要注意培养学生科学的态度。首先要有探索真理的勇气，大胆提出猜想，同时要坚持实事求是的态度，如果发现猜想不符合实际，就要有勇气修正它，没有充分理由，不轻易放弃原有的猜想。要通过不断实践检验猜想，从理论上证明猜想的正确性。

（2）类比推理

由于时差的缘故，我越来越不喜欢去美国出差试车，而且在生理和心理层面，潜意识里越来越担心试驾那种主打舒适豪华气质的车型，因为一旦被新车的从容举止所感染，我很容易犯困。而且试车地点越是阳光明媚，试驾行程越是不紧不慢，我就越容易就范。尤其是在当地时间的下午，相比在驾驶席上安逸地掌控车辆，我更乐于在副驾驶或者后排座椅的舒适区里被时差掌控，把车辆和手机调成静音状态，美美地睡上一觉。

通过类比可以发现新知识、新方法。古代鲁班师傅在山上砍树被野草划破皮肤后，他发现野草边缘上有许多锋利的锯齿，类比设想发明了木工的锯子。数学的发现中也常从类比开始。在类比中要抓住事物的本质属性，找到他们内在的联系才能进行类比，如平面图形和空间图形有相似的特征，平面上两条直线不能围成一个有限图形，三条直线可以围成一个三角形；在空间将直线换成平面，出现三个平面不能围成有限图形，四个面可以围成一个四面体。从两者以数目最少的简单分界为元素所围成的图形看，三角形与平面的关系、四面体与空间的关系是一致的，存在类比关系。可以从平面图形的性质类比猜想立体几何的性质。在类比中一定要向学生说明，这是合情推理的一种猜想，它的正确性一定要经过证明才能成立。

（3）从特殊化到一般化的方法

在寻找较大一类范畴的问题的解法遇到困难时，可以把这一范畴缩小到比较特殊的情况，从而可以发现一般情况的解法。即从对象的一个给定的集合，转而研究包含在这集合的"特殊化"的探索法，由于矛盾的普遍性寓于特殊性中，通过特殊化，可以打开解决一般问题的思路。这种特殊化方法是我们探求复杂问题的解法的一种有力的手段。如从任意n多边形引进一个限制（所有边和角相等），即对正n边形进行研究，进而对n=3的情况，即等边三角形进行研究。特殊化的发现的好处是：1从逻辑上看，概念的外延缩小，则它的内涵增多，研究起来比较容易；2从认识论上看，复杂的问题经过特殊化后，由浅入深，比较符合人的认识过程；3从方法论上看，讲复杂问题特殊化后就可以解决比较简单的问题，进而发现解决复杂问题的解法。

（4）推广的方法

在探求新知识时，人们总是从旧有的知识出发，对旧有知识加以更系统深入的分析和研究，在此基础上谋求更多的新的知识的发现，称作"推陈出新"，常用的方法是推广，即从一个小范畴的事物的研究过度到包含这一小范畴的事物的更广阔的大范畴的事物的研究。在数学上，对一个定理可以从不同的角度来考虑推广新的结论。在代数方面，可以对式子中的一些特定的量进行推广。

四、逐步逼近的过程

认识是一个过程，是思维对客体的永远接近。

某些新颖的数学问题，难以找到某个题型为仿解的基础，但如果可以判断，该问题的"解"可以按某种方式一步步地逼近之；或者，它的"解"可能存在的区域，通过某一种设计合理的方式，从无限集可结到一个有限集，进而还可以一次次地把"解"的可能存在域缩小、再缩小……，以尽量减少直接检试的个数、次数。这是我们这里所说的逐步逼近的又一层意思。

1.顺推

从已知条件和有关的知识出发，你能推出些什么？再进一步呢？分别考虑各个部分，各个细节，看能否在往前推进一点？

顺推，犹如从石堆里抓老鼠时，可以在通过各种信息估计老鼠所藏的地方（结论之所在），把石头一块接一块地搬开（这就更接近目标了！），以达到最求的目的；又如攻城堡时，把外围的零星据点一个接一个地拔除，以最终攻克城堡。顺推时，要注意瞄准结论，即我们将"奔向"的“目标”。

2逆溯

逆溯就是从结论出发，向条件逐步推倒，即不断提问：通常有哪些途径，可以算出所要求的某一个量，或推导出所需要的一个结论？在逆溯一步！

逆溯是围绕着目标的思考。犹如指挥中枢在作战地图前集中讨论战斗方案时，总是围绕着将要被攻克的目标进行多方面、多角度的分析一样。逆溯时，要时时对照条件。犹如制订作战方案时，不能超越本身的条件一样。

以上借分析例题阐发思想方法，用思维规律启示引导解题过程，旨在让更多同行参加探讨，让数学解题更具科学性。

[1]朱匀华主编.中学数学思考方法与解题途径.中山大学出版社，1984.8.

[2]苏式冬主编.中学数学研究[M].广东教育出版社，1990.12.

（作者单位：云浮市中等专业学校）

（编辑 王旸）