基于TEM图像的炭黑在聚合物基体中分散性的定量表征
姜兆辉,付 鹏,金 剑,肖长发,李 鑫,孔令熙
(1天津工业大学 改性与功能纤维天津市重点实验室,天津300160;2中国纺织科学研究院生物源纤维制造技术国家重点实验室,北京100025)
基于TEM图像的炭黑在聚合物基体中分散性的定量表征
姜兆辉1,2,付 鹏2,金 剑2,肖长发1,李 鑫2,孔令熙2
(1天津工业大学 改性与功能纤维天津市重点实验室,天津300160;2中国纺织科学研究院生物源纤维制造技术国家重点实验室,北京100025)
采用熔融共混-母粒稀释技术并辅以高效动态混合器制备了聚丙烯/炭黑薄膜。基于TEM图像定性和定量表征了炭黑在其中的分散与分布。首次将Image J图像分析软件引入分析过程,获取了粒子数目、粒子表面密度、平均粒径及其分布等统计数据。结果表明,粒子平均直径为0.2μm,当量直径服从多峰非正态分布。Origin拟合结果表明,粒子面积服从对数正态分布。此外,将TEM图像所呈现的定性信息与描述混合体系混合效果的森下氏分散指数(I)、偏斜度(β)及莱西指数(M)结合起来,对炭黑粒子在聚丙烯基体中的分散与分布进行了定量表征。森下氏分散指数为0.985,表明炭黑粒子在基体中的空间分布均匀;偏斜度为0.0014,意味着薄膜中炭黑粒子分散良好及分布均匀;莱西指数为0.987,表明炭黑粒子与聚合物基体混合效果较好。
聚丙烯;炭黑;定量;TEM;Image J;分散;分布
炭黑是由芳香族化合物在一定的控制条件下不完全燃烧或热裂解而生成[1,2]。炭黑可广泛应用于橡胶工业、纤维工业[3]、油墨颜料、塑料喷涂及复合材料增强等领域,因此激起了学者的浓厚兴趣。总体而言,炭黑以三种形式存在:能够稳定存在的最小单元——直径为20~100nm的初级粒子;由于较大的比表面积,初级粒子极易团聚成直径为0.1~0.8μm的次级粒子——聚集体;三级粒子通常指直径达1~1000μm的团聚体,这归咎于范德华力和聚集体表面电荷之间的相互吸引[4]。炭黑理想的分散状态为:所有的团聚体被分散为聚集体,且聚集体之间互相分离,每个聚集体表面均被聚合物基体所包覆。值得注意的是,聚集体是炭黑的特征单元,也是炭黑分散达到的理想目标。因此,将团聚体分散为聚集体或初级粒子并使这些较小的粒子均匀分布是混合过程的关键。
炭黑在橡胶工业中应用极其成熟,因此其在橡胶中的分散性判定方法对在聚合物中的分散具有较大的参考价值。目前文献报道的判定方法有干涉显微技术[5],显微照相法[6,7],电阻法[8]等。但国内外比较通用的测定橡胶中炭黑分散度的方法为ASTM D 2663—08标准中的A和B法,其中A法是定性测量法,B法是定量测量法。其中定量测量法类似于标准ASTM D 3015—95“塑料共混物中颜料分散的显微镜测试方法”、ASTM D 5596—94“聚烯烃土工合成材料中炭黑分散的显微镜分析测试方法”、ISO 11420:1996“聚烯烃管材、管件及混合料中炭黑分散度的测定方法”、ISO 13949:1997“聚烯烃管材、管件及混合料中颜料分散度的测定方法”以及GB/T 18251—2000“聚烯烃管材、管件及混合料中颜料或炭黑分散的测试方法”。
这些显微镜测试分析的缺点在于,它们仅限于二维分析,只能分析聚集体投影。原则上讲,通过从不同角度观察聚集体并以此法重建三维聚集体结构来放大二维分析,但是这项技术尚未成熟,而且难以进行三维聚集体形状统计分析。因此,基于显微图像,建立表征炭黑分散性的参数模型可作为显微照相法的有益补充。
本研究采用熔融共混-母粒稀释技术制备了聚丙烯/炭黑薄膜。其中在熔融共混阶段引入了自制的专用于高黏流体和极少量添加的高效动态混合器。本工作提出的定量表征炭黑分散性的方法一方面建立炭黑在聚合物中分散性的评价体系,另一方面对高效动态混合器的混合效果作一评估。本工作将透射电子显微镜(TEM)图像所呈现的信息与描述混合体系混合效果的几何参数结合起来,对炭黑在聚丙烯薄膜中的分散做了系统研究。
1 实验
1.1 实验原料
聚丙烯切片,北京燕山石化有限公司,熔融指数(MI)=2~4;聚丙烯黑色母粒,广东东莞虎门金彩色料厂提供,炭黑为30%(质量分数,下同)。所用原料均未作任何处理。
1.2 聚丙烯/炭黑薄膜制备
薄膜制备装置如图1所示。聚丙烯熔体和母粒熔体分别由单螺杆A和B熔融。经计量泵4和5计量后,熔体被注入动态混合器后经模具挤出形成薄膜。动态混合器具有轴向和径向的弧形腔室,这些弧形腔室由带有球穴的螺杆与同样具有球穴结构的套筒所组成。伴随着螺杆的转动,熔体细流被分割为极小的熔体单元,并且能够在切线和轴向重新分布和组合。该动态混合器的混合基于两个原理:由于高剪切作用而产生的分散混合作用和由于将流体分为无数个小单元而产生的分配混合效应。分配混合主要是改善组分的空间分布状况,而分散混合能在最小的应力和变形情况下将聚集体分散。由于混合料环的剪切能力,即使是小容量的混合或是黏度差异大的添加剂以1∶100的比例加入也能够达到高度均匀的混合或分散的效果。本研究制备了炭黑质量分数为2.2%的薄膜用于定量表征。薄膜挤出工艺见表1。

图1 高效动态混合装置示意图Fig.1 Schematic diagram of mixing process

表1 薄膜制备条件Table 1 The operation conditions to prepare films
1.3 薄膜TEM表征
用于TEM观测的样品在不同的膜挤出时间点随机选取。借助超声钻石刀将薄膜制成厚度为100nm左右的超薄切片,然后将所得切片置于具有支持膜的铜网上。在日立H-800型透射电子显微镜上,将加速电压调整为200kV,观察膜样品的微观结构。依据标准ASTM D5596—94,至少需要三张TEM图片用于统计分析。
2 结果与讨论
2.1 TEM粒径及其分布
图2为薄膜的TEM图片。由图2可以看出,深色的背景中遍布许多炭黑聚集体,但聚集体粒径大多小于1μm,属于次级粒子的粒径范围,也是炭黑稳定存在的结构单元。这表明炭黑在聚丙烯基体中分散良好,同时也满足了纺丝过程中对无机粒子粒径小于1μm的要求[9]。利用图片分析软件Image J,分析了这些区分度较大的TEM图片。具体步骤如下:首先以合理的图片格式打开欲处理图片,并将图片类型转化为8-bit。依次进入“Analyze/Set Scale”,在对话框中校准图片的比例尺。然后选择工具“Polygon selections”来圈定粒子的边界。最后点击“Analyze/Measure”,这时粒子面积会呈现在一文本框中。依次逐一操作,将得到图片中所有粒子的面积[10,11]。粒径大小及其分布数据列于表2。

图2 薄膜TEM图像Fig.2 TEM images of the film
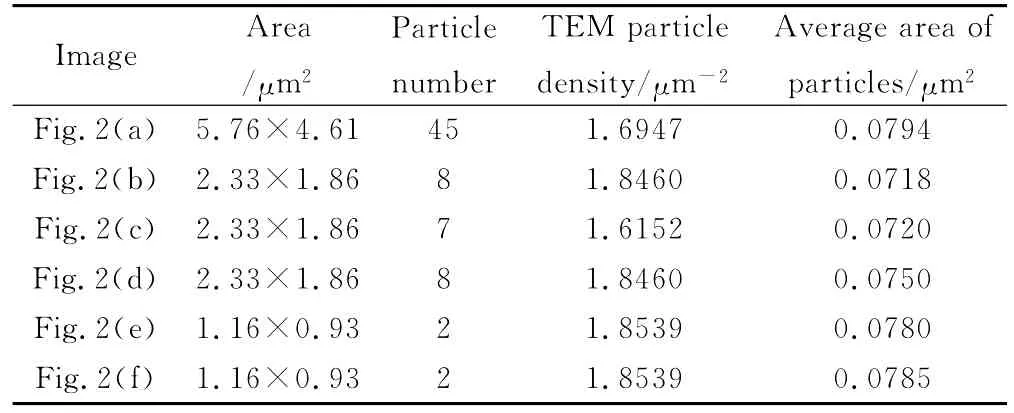
表2 聚合物基体中炭黑粒径及其分布Table 2 TEM particle size and distribution analysis ofCB particles in polymer matrix
表2涵盖了粒子个数、粒子单位面积密度及粒子平均大小。炭黑含量一定时,粒子单位面积密度越大,平均粒径越小,则炭黑在聚合物基体中的混合效果越好。如果粒子数目足够多,粒子单位面积密度可用于定量描述炭黑含量,但它不是绝对的评价标准。例如,根据粒子单位面积密度,图2(a)中粒子混合效果优于图2(c),然而考虑到粒子平均大小,图2(a)混合效果较差。这点分歧源于粒子大小阈值的选取,因此,选取合适的阈值是本方法的关键。
根据文献[12],大部分粉体和分散体系,尤其是粉碎法制得粉体大都服从对数正态分布。因此,对粒子平均面积分布进行了对数正态分布拟合,其曲线示于图3。粒子面积与其分布频率之间的拟合方程如下:

式中:Y为频率;X代表粒子面积。

图3 粒子面积分布Fig.3 The relationship between the area of particles and frequency
粒子的当量直径通过下式转化:

式中:R和S分别代表粒子的当量直径和面积。
粒子当量直径分布如图4所示。由图4可见,粒子的当量直径服从多峰非正态分布。平均粒径由下式可得:

式中:d是平均粒径;f(x)为面积分布;Ymax和Ymin分别代表概率的最大和最小值。在Origin中通过积分操作,d=0.24μm,这与通过以下方程:

图4 粒子当量直径分布Fig.4 The relationship between equivalent diameter of particles and frequency

计算而得d=0.25μm相一致。式中:Xi为粒子直径;N为粒子数目。
TEM粒径及其分布能客观的表征炭黑粒子的分散和分布。尽管这项工作繁琐且结果依赖于对最小粒子的定义。如果运用恰当,TEM粒径及其分布是定量表征炭黑粒子在聚合物基体中分散和分布的有效方法。
2.2 森下氏分散指数(Morisita’s Index)
森下氏分散指数(I)重点强调炭黑粒子的空间分布,其数学表达式如下[4,13]:

式中:Q为图片数量;N为粒子总数;ni为第i张图片中粒子数目。根据表2中TEM粒子单位面积密度数据,将图片归一化为5.76μm×4.61μm,因为式(5)中要求图片面积相同。每张图片中粒子的当量个数见表3。

表3 各图像中粒子数目Table 3 The number of particles in every image
基于方程(5),经计算森下氏分散指数为0.985,这意味着炭黑粒子在聚丙烯集体中分布均匀。如果I小于1,这暗示着炭黑粒子完全分离且分布均匀;如果I等于1,这意味着粒子分离且随机分布;如果I大于1,这预示着炭黑粒子发生了聚集甚至团聚。当I从小值逼近1时,说明粒子分布均匀且I值越大分布越均匀;当I从大值逼近1时,说明粒子发生聚集且I值越大聚集越严重[4]。由方程(5)可知,表达式仅仅涉及图片数量和粒子数量,并未涉及粒子大小,森下氏分散指数主要用于描述粒子的空间分布。因此,森下氏分散指数可作为定量表征炭黑粒子在聚合物基体中空间分布均匀性的指标。
2.3 偏斜度(Skewness-Quadrat Method)
偏斜度(β)源自于偏斜度方法,可由以下方程定义:
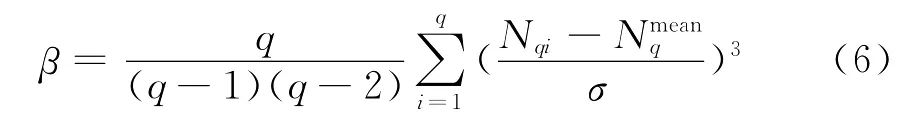
式中:q为所研究方格的总数;Nqi为第ith个方格中的粒子个数;Nmeanq为每个方格中的平均粒子个数;σ是粒子个数分布的标准差。因为偏斜度考虑到了粒子数目及其空间分布,因此它综合反应粒子的分散和分布效应,已经用于描述沙滩上蚁穴的分布或较小粒子的分散[14]。如果粒子分散良好、分布均匀,每个方格中的粒子数目呈哑铃型分布;反之,呈非对称分布。偏斜度指平均值周围的不对称度,其值分布于0到无穷大之间,值越小分散越好、分布越均匀。
图5为TEM图像的方格划分图。如图5所示,图片被分成许多方格,这取决于粒子平均大小。一般而言,方格大小约为粒子平均大小的2倍。如表2所示,粒子平均面积为0.0794μm2,故将4.05μm×4.05μm面积分成10×10方格。数出每个方格中的粒子个数,为减小边缘效应,只将位于方格内或与方格左边、底部接触的粒子计算在内。然后,偏斜度按方程(6)计算得出。

图5 10×10方格TEM图像Fig.5 TEM image with a grid of 100quadrats

表4 图像偏斜度数据Table 4 Skewness analysis for image
偏斜度数据列于表4。由表4可知,本研究中偏斜度值较小,说明薄膜中炭黑粒子具有较好的分散及分布。然而,实际运用中两个关键点需要注意,其一方格大小的选取;其二偏斜度适用于粒子含量相同的情况。选取恰当的方格大小,偏斜度可用于评价相同含量炭黑薄膜的混合效果。
2.4 莱西指数(Lacey Index)
混合的两个极端:完全分离和完全随机。对前者而言,任一由混合物中分离出来的单一组份接近纯净物。对后者而言,由混合物的各部分分离出任一组分的机会均等。参考文献[15],对于完全分离的混合物,方差表达式如下:

式中p和q分别代表两种组分所占比例。对于完全随机分布的混合物,方差(S2R)以下式表达:

式中N为粒子数目。可以将样品方差作为衡量混合质量的指标。样品方差方程如下:

式中:N为样品个数;yi为某一组分在样品中所占比例的第ith个值为某一组份在样品中所占比例平均值,其可通过下式计算:

本研究中,yi代表炭黑粒子含量,其值通过热重法测出,分别为2.11%,2.20%和2.14%。莱西指数定义如下:

莱西指数在0~1之间。当混合物处于完全分离状态时,其值为0;当混合物处于完全随机状态时,其值为1。实践证明,莱西指数位于0.75~1.0之间[16,17]。由于其简便易行,莱西指数常用于指导实际生产。对于整个样本空间,为炭黑粒子的理论含量[18-20]。根据方程(11),经计算M为0.987。M值越大,混合效果越好。尽管莱西指数常用于评价两种粒状料的混合水平,但用于表征炭黑在聚合物基体中的分散与其他表征方法有较好的一致性。
3 结论
(1)采用熔融共混-母粒稀释技术,辅以高效动态混合器制备了聚丙烯/炭黑薄膜。基于TEM图像定性和定量表征了炭黑在其中的分散与分布。炭黑在聚丙烯基体中的粒径明显小于1μm。
(2)借助Image J图像分析软件,对粒子数目、TEM平均粒径及粒子表面密度进行了分析,结果表明TEM平均粒径为0.2μm左右,粒子面积分布服从对数正态分布,当量直径分布服从多峰非正态分布;森下氏分散指数为0.985,表明炭黑粒子在基体中的空间分布均匀。偏斜度为0.0014,意味着薄膜中炭黑粒子分散良好及分布均匀。莱西指数为0.987,说明炭黑粒子与聚合物基体混合效果较好。
(3)TEM图像所呈现的定性信息与描述混合体系混合效果的几何参数结合起来,可客观、全面的表征炭黑粒子在聚合物基体中的分散与分布。
[1] MATTEW F S,VADIM F L.Characterization of non-aqueous dispersions of carbon black nanoparticles by electrochemical impedance spectroscopy[J].J Electroanal Chem,2005,577(1):67-78.
[2] HUANG J F,SHEN F,LI X H,et al.Chemical modification of carbon black by a simple non-liquid-phase approach[J].J Colloid Interf Sci,2008,328(1):92-97.
[3] 张慧慧,郭利伟,邵惠丽,等.炭黑填充Lyocell纤维的制备及其用于炭纤维原丝的研究初探[J].新型炭材料,2004,19(3):172-178.
[4] KIM D J,SEO A H,HONG K H,et al.Effects of dispersing agents on dispersity and mechanical properties of carbon black/PET[J].Polym Eng Sci,1999,39(1):500-507.
[5] 安阳.用干涉显微技术测量炭黑分散度[J].现代橡胶技术,2006,32(6):40-41.
[6] 卢尚斌,王晓辉.显微照相法测定炭黑分散度的研究[J].橡胶工业,1999,46(7):421-424.
[7] 汪传生,祝卫国.混炼胶中炭黑分散度测定方法的改进[J].橡胶工业,2004,51(12):755-758.
[8] 占部诚亮,赵可申.用电阻法测定炭黑的分散度[J].橡胶译丛,1987,(6):69-76.
[9] 裴运同,李恒泰.丙纶强力丝专用色母粒的研制[J].塑料工业,1997,(4):85-87.
[10] JACQUIR.Introduction to image J[J].Biomedical Imaging Research Unit,2009,(9):1-19.
[11] TONY J C.Introduction to image j for light microscopy[J].Microsc Microanal,2007,13(2):1674-1675.
[12] HWANG S I,CHOL S I.Use of a lognormal distribution model for estimating soil water retention curves from particle-size distribution data[J].J Hydrol,2006,323(1-4):325-334.
[13] NAKAO Y,YABUTA M,TOMINAGA A.The relation between the dispersion state of polymer microspheres in coatings and film properties[J].Prog Organic Coat,1992,20(3):369-381.
[14] KARNEZIS P A,DURRANT G,CANTOR B.Characterization of reinforcement distribution in cast al-alloy/sicp composites[J].Mater Charact,1998,40(2):97-109.
[15] TZAMTZISL S,BAREKAR N S,BABUA N H,et al.Processing of advanced Al/SiC particulate metal matrix composites under intensive shearing-a novel Rheo-process[J].Composites Part A,2009,40(2):144-151.
[16] RHODES M J,WANG X S,NGUYEN M,et al.Study of mixing in gas-fluidized beds using a DEM model[J].Chem Eng Sci,2001,56(8):2859-2866.
[17] TASIRIN S M,KAMARUDIN S K,HWEAGE A M A.Mixing process of binary polymer particles in different type of mixers[J].Modern Applied Science,2009,3(6):88-95.
[18] ALHWAIGE A A,TASIRIN S M,SOWEDAN A M,et al.Study the homogeneity of mixing a binary polyethylene granular mixture in fluidised bed mixer[A].Proceedings of the World Congress on Engineering and Computer Science[C].San Francisco:International Association of Engineers,2008.
[19] ZHAO Y Z,JIANG M Q,ZHENG J Y.Discrete element simulation of the segregation in brazil nut problem[J].Acta Physica Sinica,2009,58(3):1813-1818.
[20] ZHAO Y Z,ZHANG X Q,LIU Y L,et al.Augmenting the mixing of size-type binary granular systems in a rotating horizontal drum[J].Acta Physica Sinica,2009,58(12):8386-8393.
Quantitative Characterization Dispersion of Carbon Black Particles in Polymeric Matrix Based on TEM Images
JIANG Zhao-hui1,2,FU Peng2,JIN Jian2,XIAO Chang-fa1,LI Xin2,KONG Ling-xi2
(1Key Laboratory of Fiber Modification and Functional Fiber,Tianjin Polytechnic University,Tianjin 300160,China;2State Key Laboratory of Biobased Fiber Manufacture Technology,China Textile Academy,Beijing 100025,China)
PP/CB films were prepared with the method of melt blending-masterbatch dilution method,assisted by high-efficiency dynamic mixer.Based on TEM images,the dispersion and distribution of CB particles were characterized quantitatively and qualitatively.The image analysis software,Image J,was introduced to achieve particle number,particle area density,particle size and their distribution.It turns out that the mean diameter of particles is about 0.2μm and equivalent diameter subjects to non-normal multi-peak distribution.The result from origin fitting confirms that area distribution of particles approximately follows lognormal distribution.Quantitative and qualitative characterization were conducted combining TEM images with Morisita’s index (I),Skewness(β)and Lacey index(M)which were used to depict mixing effect.Morisita’s index is 0.985,which demonstrates a uniform distribution of CB particles.The value of Skewness(0.0014)informs us that CB particles in polymer matrix are provided with good dispersion and uniform distribution.Lacey index equals 0.987,which indicates that CB particles and polymer matrix are mixed well.
polypropylene;carbon black;quantitative;TEM;Image J;dispersion;distribution
TQ317.2
A
1001-4381(2011)10-0072-06
科技部国家科技支撑计划(2009BAE75B01)
2010-10-04;
2011-03-07
姜兆辉(1982—),男,博士生,从事高聚物结构与性能研究,联系地址:北京市朝阳区延静里中街3号中国纺织科学研究院研究开发中心(100025),E-mail:tjjzh_2005@163.com

