基于模式与熵的随机序列研究

崔圆圆 北京邮电大学电子信息工程专业 100876

基于模式与熵的随机序列研究

崔圆圆 北京邮电大学电子信息工程专业 100876

本文从双色球开奖结果出发，探讨真随机序列中暗含的“模式”：真随机序列有时表现得并不那么“随机”。这是因为人们认为，随机应是无序的。事实证明，并非如此。另一方面，人为产生的伪随机序列，大多经过了消除重复的步骤以使序列本身较为“随机”——看起来是无序的。本文使用Mersenne Twis算ter 法产生伪随机序列，测试这种人为因素对随机序列统计特性的影响。为了进一步研究“无序”序列与随机序列的差异，本文基于熵，提出了一种简便的伪随机数发生器。通过对有序序列进行次数可控的交换来逐步实现无序化。对无序化后的序列进行均匀性和图像加密测试。通过无序的方法产生的序列，其随机性在一定范围内是可以信赖的。

真伪随机序列;模式;熵 ;Mersenne Twister算法;图像加密

1.形形色色的随机数

在自然界和人类社会中存在着两类现象，确定性现象和非确定性现象。前者在一定条件下必然发生；对于后者，其结果的样本空间非但并不唯一，大多数时候甚至难以计量。非确定性现象，或者说随机现象，经过大量的重复试验或观察，总能表现出一定的统计规律性。随机数根据其产生机理，可分为两种：真随机数与伪随机数。前者由物理采样方法得到，后者来自于数学计算。

2.随机序列与模式

2.1 真随机数及其特征

真随机数源有很多，包括人为随机源、设备随机源、电路中的热噪声和散粒噪声，等等。电脑的操作系统就能够实现对如键盘随机性、鼠标随机性、中断随机性等的统一控制，以产生符合要求的随机数。即使是真随机数发生器的设计者，也不可能知道实际生成的随机序列的内容，生成的随机数是真正无法预测的。

2.2 真随机与假模式

2.2.1 预测的模式

随机现象的本质是不确定性。研究表明，“我们在不确定局面下进行评估和选择时，常常会依赖于直觉”。面对随机序列，我们所要做出的判断并不会威胁自身的安全，仅仅是个小小的判断。这时候，模式的思维就占了上风。

2.2.2 双色球中的幸运

在中国，目前双色球是一种较流行的博彩方式：投注区分为红球号码区和蓝球号码区，红球号码范围为01～33，蓝球号码范围为01～16。双色球每期从33个红球中开出6个号码，从16个蓝球中开出1个号码作为中奖号码，双色球玩法即是竞猜开奖号码的6个红球号码和1个蓝球号码，顺序不限。考虑到16是2的四次幂，便于后文的二进制计算，本文取每一期的蓝球号码作为真随机序列。

毫无疑问，每一次的蓝球数字都是随机产生的。现在，让我们再来看看前一节所提到的ABCDE五个数字序列。印象中最为随机不可预测的序列，竟然表现出了惊人的“模式”。不得不相信，这些模式，仅仅是凑巧的结果。一方面，概率学的知识告诉我们，产生任何一种排列，都是有可能的，而这些模式，只是无数可能排列中的一种而已；另一方面，真随机序列，原来有时候看起来并不那么“随机”。

2.2.3 统计性验证

用于描述随机序列的两个主要指标就是期望和方差。数学期望体现了随机变量的真正平均，而方差则代表随机变量的取值与其方差的偏离程度。

对于理想的从1～16等可能取值的随机序列，其数学期望和方差分别为：

取最近200期的蓝球开奖结果，计算其平均值与方差：

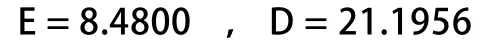
可见，即使没有数量庞大的样本（只取了200个），真随机序列在统计特性上的表现，仍是十分优越的。真随机序列中暗含的“模式”，让它看起来不那么随机了。

2.3 伪随机序列

与真随机序列相对的，就是假随机序列。一般计算机中使用的伪随机序列，都是通过递推公式计算得来。这种生成装置，称为伪随机数发生：由一个初始状态（种子）开始，通过一个确定的算法来生成随机数。

另一种广泛使用的PRNG，是Mersenne Twister算法（马特赛特旋转演算法）。

1997 年，松本和西村开发了这一基于有限二进制字段上矩阵线性再生的伪随机数算法。它的算法随机性好，易实现，占用内存少，产生随机数的速度快、周期长，且具有623维均匀分布的性质。 在MATLAB v7.7 及以上版本中，通过调用RandStream类，就能产生基于MT的伪随机数。

2.4 两种随机数的比较

将Matlab自带的随机序列生成器设为“mt19937ar”，便可以得到基于MT算法的伪随机序列。为了与双色球的真随机数作比较，产生多组200个同区间均匀分布的伪随机数。计算数学期望与方差，可得：

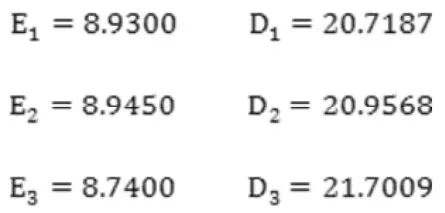
可以看到，Matlab产生的伪随机数偏离理想均值8.5的程度比双色球大，其波动却相对较小。

使用随机数生成算法连续生成的2 0 0个随机数，耦合成199个像素坐标值。Dn表示第n个像素点，以此衡量数据的均匀性。作图后可见，两者的均匀性相似。如果取值空间更大，而不是1至16，应当会出现一定的差异。

3.基于熵的伪随机序列发生器

3.1 物理熵

1850 年，德国物理学家鲁道夫·克劳修斯首次提出熵的概念，用来表示任何一种能量在空间中分布的均匀程度。一个体系的能量完全均匀分布时，这个系统的熵就达到最大值。系统的熵，只能逐渐增大或保持不变，而不可能逐渐减小。在物理学中，熵代表着系统的无序性。越是均匀无序的系统，其熵值越大。

3.2 信息熵

信息论的创始人香农，率先将熵的概念进行了泛化，引入信息熵。对于有限离散随机变量集合，当集合中的等概率发生时，熵达到最大值。对于随机序列，当取值均匀分布时，熵达到最大值。熵标志着系统的无序性，当序列变得无序，熵也不断增大，逼近均匀分布。

3.3 基于熵的发生器

构建一个序列，由四个从0到255的连续升序排列（0,1,2,...255）组成。显然，这一序列是非常有序的。根据前一小节的分析，如果不断打乱其排序，序列的熵就会不断增加，逼近最大值。这时，就有可能得到了一个伪随机序列。

在原序列基础上，每次随机选取两个序号，交换其值，进行实验。根据期望和方差的定义，由于打乱后的序列，其各个数字的数量维持在4不变，因此均值和方差与理想序列相同。

3.3.1 均匀性测试

按照第二部分中介绍过的均匀性衡量方法，取序列的前256个值作图。记k为交换的次数，分别做出k=0,100,200,300, 400,500时的均匀性分布图。

未做交换时，原图是一条直线。随着k的值不断增大，点越来越分散。k=500时，仍能看出原图的痕迹。对于使用这种扰乱的方法构造的1024个数字组成的序列，在交换500次时，随机性仍不理想。

当交换次数达到600时，点的分布已找不到原始的规律；随着交换不断增加，均匀性状况不再改变。对于一个长度为2n的序列，交换n次时，可基本无序。

3.3.2 无序程度测试

在未进行交换时，1024个点，每个都在自己的初始位置。现每交换100次后，测试仍在初始位置的点的个数，它表现出了明显的下降趋势，并且在3200次之后开始波动，不再单一递减。可以推测，对于长为n的序列，当交换3n次时，无序状况基本稳定。

3.3.3 图像加密测试

以大小为256×256的256级灰度的Lena图像为例，明文为是一个256×256的8bit的2进制矩阵，通过reshape整合运算，将算法生成的随机数转换成为一个256×256的密钥矩阵，然后再将明文矩阵与密钥矩阵按位异或。当交换次数改变时，加密效果有所不同。交换400次后，仍能看出原图的痕迹；交换800次后，逐渐变得模糊；交换1200次后，已经完全看不出Lena的样子了。对于一个长度为n的序列，进行n次交换后，已达到较好的图像加密效果。

[1]胡细宝,孙洪祥,王丽霞.概率论·随机过程·数理统计.北京邮电大学出版社.2004年2月,第一版

[2]列纳德·蒙洛迪诺[英]著；郭斯羽译.醉汉的脚步——随机性如何主宰我们的生活.湖南科学技术出版社.2010年6月,第一版

10.3969/j.issn.1001-8972.2011.11.012

崔圆圆，北京邮电大学电子信息工程专业本科生，在读。