配电系统可靠性分析的最小割集-网络等值法①
祁彦鹏, 张 焰, 余建平, 郭 征
(1.上海交通大学电气工程系, 上海 200240; 2.上海市电力公司市东供电公司, 上海 200122)
配电系统可靠性分析的最小割集-网络等值法①
祁彦鹏1, 张 焰1, 余建平2, 郭 征2
(1.上海交通大学电气工程系, 上海 200240; 2.上海市电力公司市东供电公司, 上海 200122)
为提高复杂配电系统可靠性评估的准确性,提出一种最小割集-网络等值法,通过网络的可靠性等值简化复杂配电系统的求解过程,利用最小割集法提高可靠性计算的精度和速度,克服了传统的可靠性网络等值法没有考虑计划检修、不能计算二阶故障以及传统的最小割集法不适用于复杂配电系统等的一些不足。对RBTS可靠性测试系统进行计算的结果表明,所提方法能更真实地反映配电系统可靠性的实际状况。
配电系统; 最小割集; 网络等值; 可靠性分析; 比林顿测试系统
配电系统可靠性是指供电点到用户,包括配电变电所、高低压线路及接户线在内的整个配电系统及设备按可接受标准及期望数量满足用户电力及电能量需求能力的度量[1]。有统计资料表明,在电力系统发生的停电事故中,80%是由配电系统故障引起的[2],配电系统供电可靠性对电力用户有着极其重要的影响。
配电系统可靠性分析计算的主要方法是故障模式与后果分析法[3]FMEA(failure-mode-and-effect analysis),该方法通过对配电系统可能发生的故障事件进行后果分析,在找出系统故障模式集合的基础上得到系统及各负荷点可靠性指标。FMEA方法适用于简单辐射状配电系统的可靠性评估,而对于复杂的配电系统,直接采用FMEA方法有一定的困难。
文献[4~6]通过求取配电系统的最小路集,将非最小路上的设备故障对负荷点可靠性的影响折算到相应的最小路的节点上,对每个负荷点,仅对其最小路上的设备与节点进行计算,达到减少计算量的目的。但是随着配电系统规模的增大,求取最小路的困难也随之增加,而且其中对非最小路上设备故障影响的折算也会影响计算精度。
文献[7]通过求取配电系统的最小割集来获得系统可靠性指标。该方法将待计算的状态限制在最小割集内,大大减少了计算量。但是随着配电系统的日益复杂化,负荷点与电源点之间的供电通路可能有多个,使得最小割集的求取反而成了该法的一个瓶颈,仅使用该法已难以很好地对复杂配电系统进行可靠性评估。
文献[8~11]应用可靠性网络等值法把一个复杂的配电系统逐步简化成简单辐射状主馈线系统,有很好的适用性。文献[12]在此基础上考虑了分支馈线首端断路器的影响。但是可靠性网络等值法只能计算一阶故障,没有考虑二阶故障的影响,而且没有考虑设备的计划检修问题和母线故障的影响。
本文在文献[11]的可靠性网络等值过程中引入最小割集法的思想,提出一种最小割集-网络等值法。网络等值过程简化了配电系统可靠性计算的复杂程度,而在每一步的网络等值简化的过程中应用最小割集法,则提高了可靠性等值的计算精度与速度。在最小割集的求取过程中考虑了二阶故障、计划检修以及母线故障的影响,弥补了原可靠性网络等值法的不足,两个方法的结合,既提高了计算精度、更加真实的反映了实际配电系统的可靠程度,又没有增加太多的计算量。
1 馈线可靠性分析的最小割集-网络等值法
1.1 设备的可靠性模型
配电系统中的主要电气设备包括各种开关、熔断器、配电变压器、线路、母线等,本文对于这些设备均采用3状态的可靠性模型,如图1所示。

图1 3状态可靠性模型Fig.1 3-state reliability model
1.2 简单辐射状馈线
辐射状馈线在配电系统中占有重要地位,既可直接向用户供电,也可由多个简单馈线构成复杂的配电系统向用户供电,是复杂配电系统的组成基础。其典型结构如图2所示。
由于各馈线段由隔离开关、分段开关等连接在一起,在可靠性逻辑上可等效为串联系统上的一个馈线节点,以M表示,其中各开关的故障率可叠加到与其相连的馈线段上;各负荷支路[12]通过馈线段连接在一起,任一负荷支路发生故障,都可能引起该级馈线故障,所以也是可靠性逻辑上的串联关系,等效为一个负荷节点,以L表示。这些节点在可靠性分析中彼此独立,之间没有任何的从属关系,系统的可靠性由各节点的故障情况共同决定。

图2 简单辐射状馈线Fig.2 Simple radial feeder
另外,在该级馈线的可靠性计算中还考虑了来自上级馈线或母线故障的影响,以E表示,并串联于系统中。
于是图2在可靠性分析上可等值为图3。

图3 简单辐射状馈线的网络等值Fig.3 Network-equivalent of a simple radial feeder
1.3 最小割集-网络等值法
本文把与母线直接相连的馈线称作一级馈线,和一级馈线相连但不和母线相连的馈线称作二级馈线,依此类推,可定义n级馈线,复杂的配电系统是由多级馈线构成的,每级馈线都是一个简单辐射状馈线。本文只对配电系统中的每个简单辐射状馈线求取最小割集,计算得到它们的首端以及任一负荷支路与相应馈线段的连接点处的可靠性参数,并通过网络等值法[12]中的上行等值把复杂的配电系统最终简化成一个简单辐射状馈线,再通过下行等值求取每个负荷点的可靠性参数以及系统的可靠性指标。网络等值法是计算复杂配电系统可靠性的基本思想,用于简化复杂配电系统的可靠性计算,最小割集法应用于每一步的可靠性等值过程中,是网络等值法的基础和计算手段,用于提高可靠性计算的精度和速度。本文自始至终仅对各级简单辐射状馈线即串联支路求取最小割集。
最小割集若由n个失效设备组成,则称为n阶最小割集[14]。若要求得系统的精确解,必须进行高阶最小割集的求取,并进行最小割集不交化的处理,但是由于电力系统中的设备一般都具有较高的可靠度,计算到二阶割集便足以达到所要求的精度。
1)一阶最小割集的可靠性计算公式
设节点j为图3所示的等值简单辐射状馈线上的任一负荷支路与相应馈线段的连接点,由于所有的负荷节点以及馈线节点可靠性上的逻辑串联关系[12],可得该点所对应的一阶故障率λj、故障持续时间rj以及年停电时间Uj的计算公式如下:
(1)
(2)
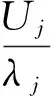
(3)

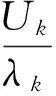
设联络开关成功闭合的概率为pa(pa=0表示无备用电源,pa=1表示联络开关100%可靠),并设r为各自设备的故障修复时间、ra为联络开关的倒闸操作时间、rd为分段开关操作时间,并且有r≥ra≥rd。
①故障点与负荷节点j之间未设分段开关
在此种情况下故障设备不能被隔离,rE、rQF、ri、rk为故障设备的修复时间r。
②故障点与负荷节点j之间设有分段开关
故障点位于电源侧时,则节点j可能通过备用电源继续供电,故取联络开关的倒闸操作时间ra与故障设备的修复时间r的组合值作为故障持续时间[12]:rapa+r(1-pa)。
故障点远离于电源侧时,仅分段开关打开即可,故障持续时间取为分段开关操作时间rd。
2)二阶最小割集的可靠性计算公式
二阶最小割集可分为无计划检修和计划检修两类,下面分别阐述。
①无计划检修的二阶最小割集
无计划检修的二阶最小割集中,两故障设备只是简单的并联关系[13],其可靠性参数计算公式如下:
(4)
(5)
(6)

②计划检修时的二阶最小割集
有计划检修的二阶最小割集是指一个设备在检修状态中,另一个设备发生故障,从而导致负荷节点j供电终止的情况,相当于一个条件概率[13],其计算公式为(假设设备1处于计划维修状态):
(7)
(8)
(9)

实际上,二阶割集仅对双电源供电或带有联络开关的馈线有用,若某一条馈线仅由单电源供电,则只求取一阶割集即可。
3)简单辐射状馈线首端FT与负荷点Lp处的等值可靠性参数的计算
求得简单辐射状馈线所有的一阶及二阶最小割集后,即可按照网络等值[11]的思想对其进行可靠性的分析计算,主要有首端FT以及负荷点Lp处的可靠性参数计算两个方面,其中前者是上行等值的基础,而后者则是下行等值的基础。
①首端FT的可靠性参数计算
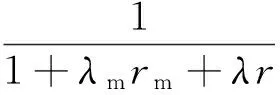
(10)
(11)

(12)
式中:故障持续时间rQF、ri、rk为隔离开关的操作时间rd,其余参数含义与前相同。
若馈线首端没有断路器,则在式(10)、(11)中令λQF=0,pQF=0,其中的故障持续时间ri、rk的计算方法为:故障设备与首端之间没有分段开关时,取各自的故障修复时间r;故障设备与首端之间设有分段开关时,取分段开关的操作时间rd。
②负荷点Lp处的可靠性参数计算
求得简单辐射状馈线所有的一阶割集和二阶割集的可靠性参数后,即可计算各负荷点Lp处的可靠性参数,其计算公式如下:
(13)
(14)
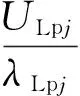
(15)
式中:ULpj、λLpj、rLpj分别表示负荷点Lpj处的等值年停电时间、等值平均故障率、等值平均故障持续时间,p、q分别指无计划检修及有计划检修时的二阶最小割集的个数,其余参数含义与前相同。
2 复杂配电系统可靠性分析的最小割集-网络等值法
复杂的配电系统是由多条简单辐射状馈线构成的,如图4(a)所示。与母线直接相连的简单辐射状馈线(称为一级馈线)上负荷节点处连接的是另外一条简单辐射状馈线(称为二级馈线),而在该二级简单辐射状馈线的负荷节点处又连接了一个简单辐射状馈线(称为三级馈线),依此类推,就构成了一个复杂结构的配电系统。处理该类复杂结构的配电系统,可通过最小割集-网络等值法的上行等值、下行等值过程来求取,两者的具体过程分别阐述如下。
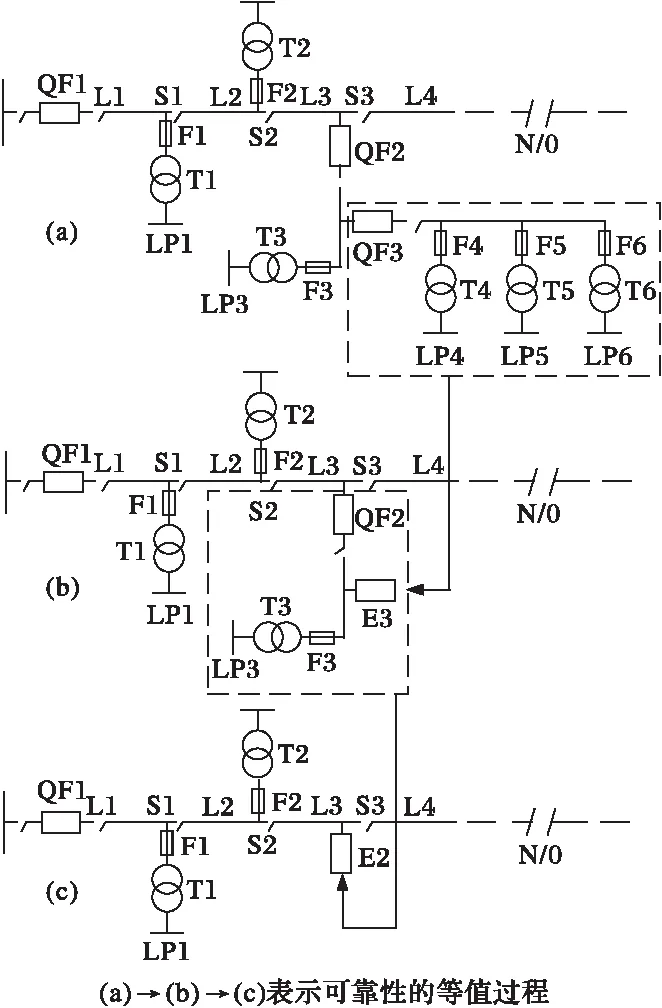
图4 复杂配电系统的最小割集-网络等值Fig.4 Minimum-cutest and network-equivalentof a complex distribution system
2.1 上行等值过程
上行等值的过程其实就是化复杂配电系统为简单辐射状馈线的过程,其目的是把一级馈线上所连接的所有二级馈线,以及二级馈线上所连接的所有三级馈线等等逐级向上等值为一级馈线上的一个个负荷节点。可先通过最小割集法,求取每条简单辐射状馈线首端处的可靠性等值参数,从而将每条简单辐射状馈线等值为上级馈线的一个负荷节点,这样逐级简化,最终即可将一个复杂的配电系统简化为一个或多个一级简单辐射状馈线,其可靠性参数的计算公式和首端FT的可靠性参数计算公式(10)~(12)相同。
2.2 下行等值过程
通过最小割集法求得一级简单辐射状馈线上各负荷节点与馈线节点的连接点处的可靠性参数后,将该可靠性等值参数作为上级馈线对下级馈线的影响串联在二级馈线中,如图3中的E所示,然后再次运用最小割集法求取该二级馈线负荷节点与馈线节点的连接点处的可靠性参数,依此类推,可求得所有负荷节点与馈线节点的连接点处以及原始负荷点处的可靠性参数,其可靠性参数的计算公式和负荷点Lp处可靠性参数计算公式(13)~(15)相同。
求得所有负荷点Lp处的可靠性参数后,即可计算系统的可靠性指标,计算公式见文献[2]。
3 算例分析
3.1 算例及其原始数据
本文采用比林顿可靠性测试系统RBTS(roy billinton test system)可靠性测试系统bus6[14,15]的馈线4作为算例,系统的单线图如图5所示。该馈线包含30段线路、23个负荷点、23个熔断器、23个配电变压器、4个断路器。各原始数据见表1~3,其中隔离开关、分段开关的操作时间为0.4 h,联络开关的倒闸操作时间为1 h。
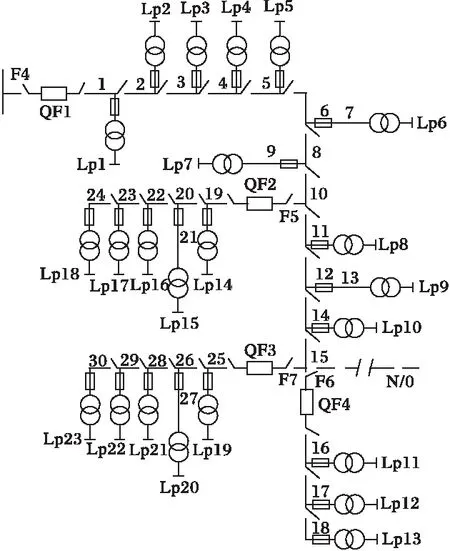
图5 复杂配电系统结构图Fig.5 Configuration of a complex distribution system表1 设备的可靠性参数Tab.1 Equipments reliability parameters
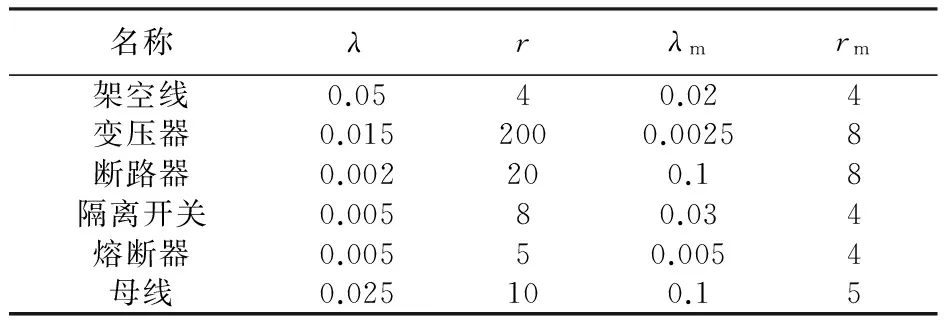
名称λrλmrm架空线0.0540.024变压器0.0152000.00258断路器0.002200.18隔离开关0.00580.034熔断器0.00550.0054母线0.025100.15
注:表中λ单位(次/年),r单位为h/次

表2 线路参数Tab.2 Feeder parameters
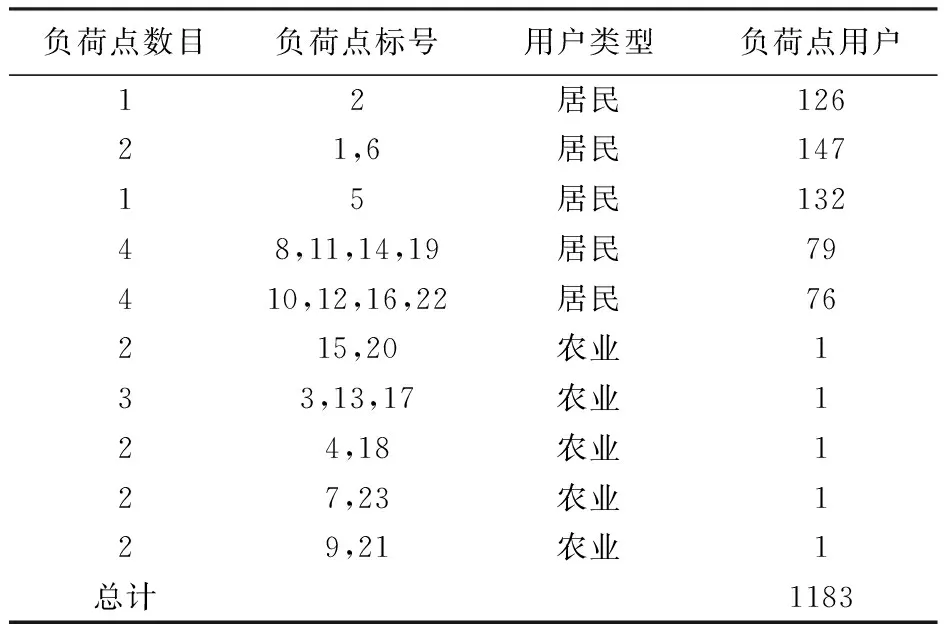
表3 负荷数据Tab.3 Customer data
3.2 计算结果及分析
在图5中,F4为一级馈线,F5、F6、F7为二级馈线,其中一级馈线F4上位于馈线F6、F7之间的连接点处设有联络开关(图5中N/0所示)与其它馈线相连,设联络线故障率为0。分以下几种情况进行可靠性的分析计算:
①不考虑母线故障,不考虑二阶故障,不考虑计划维修;
②考虑母线故障,不考虑二阶故障,不考虑计划维修;
③考虑母线故障,考虑二阶故障,不考虑计划维修;
④考虑母线故障,考虑二阶故障,考虑计划维修。
对应以上4种情况的二级馈线F5、F6、F7的上行等值及下行等值可靠性参数的计算结果示于表4。可看出4种情况下的上行等值的可靠性参数计算结果是相同的,这是因为在馈线F5、F6、F7的上行等值计算中均没有母线故障、二阶故障、计划维修的影响。在下行等值可靠性参数计算结果中,馈线F6、F7两者基本相同,但相对于馈线F5,所计算的可靠性参数值较小,主要是由于前者的位置靠近联络线而后者距离母线和联络线均较远,而馈线F5、F6两者可靠性参数值之间的细微差异主要是由于它们各自本身结构的差异所引起的。

表4 馈线5、6、7等值可靠性参数Tab.4 Equivalent reliability parameters of feeder5、6、7
注:表中λ的单位为(次/年),r单位为h/次,U单位为h/a。
表5、6列出部分负荷点处可靠性指标,表7列出系统可靠性指标。可看出,随着可靠性计算中逐步计入母线故障、二阶故障及计划维修的影响,各负荷点可靠性指标及系统可靠性指标SAIFI、SAIDI、CAIDI的值也在逐渐增加,而系统可靠性指标ASAI值则在减小,说明在配电系统可靠性评估中考虑母线故障、二阶故障,以及计划检修是必要的。
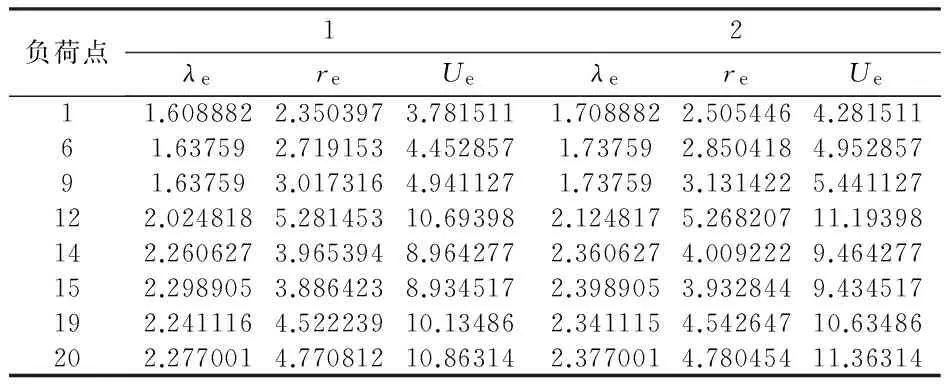
表5 部分负荷点可靠指标(计算情况1、2)Tab.5 Reliability in dices of selected load points(case1、2)
注:表中λ的单位为(次/年),r单位为h/次,U单位为h/a。
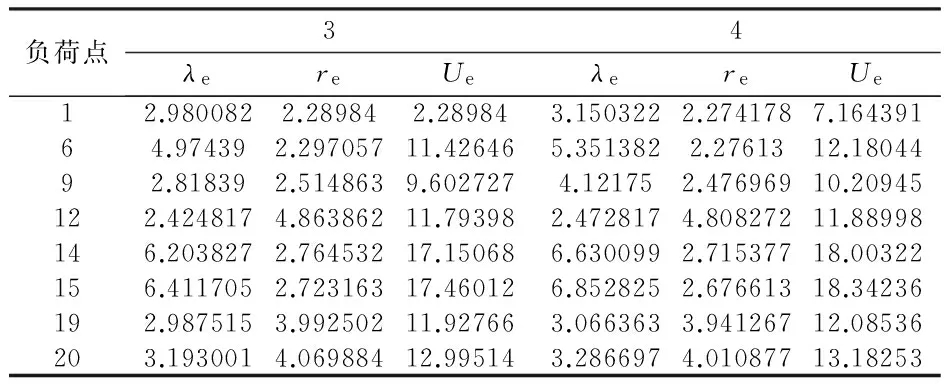
表6 部分负荷点可靠性指标(计算情况3、4)Tab.6 Reliability indices of selected load points(case3、4)
注:表中的单位分别是λ(次/年)、r(h/次)、U(h/a)。
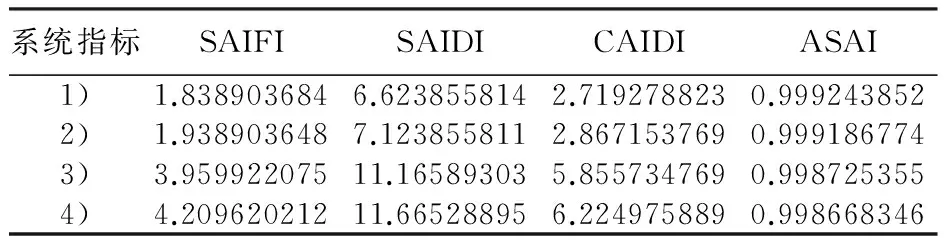
表7 系统可靠性指标Tab.7 Reliability indices of system
注:SAIFI(system average interruption frequency index)为系统平均停电频率指标,单位为次/用户年;SAIDI(system average interruption duration index)为系统平均停电持续时间指标,单位为h/用户年;CAIDI(customer average interruption duration index)为用户平均停电持续时间指标,单位为h/停电用户年;ASAI(average service availability index)为平均可用率指标。
4 结语
本文在配电系统可靠性分析的网络等值法的基础上,融合最小割集法的思想,提出了一种最小割集-网络等值法来分析计算复杂配电系统的可靠性指标,由于在可靠性的计算过程中计入了母线故障、二阶故障以及计划维修的影响,不仅提高了计算精度,而且由于把计算范围限制在了最小割集的范围中,并没有增加太多的计算量。通过考虑母线故障、二阶故障以及计划维修影响的计算结果可知,这三者对配电系统可靠性有着重要影响,在进行配电系统可靠性分析时不能忽略。
[1] 郭永基.电力系统可靠性分析[M].北京:清华大学出版社,2003.
[2] Billinton R, Allan R. Reliability Evaluation of Power Systems, 2nd Edition[M].New York: Plenum Press, 1996.
[3] 张鹏, 郭永基(Zhang Peng, Guo Yongji).基于故障模式影响分析法的大规模配电系统可靠性评估(Large scale distribution system reliability evaluation based on failure mode and effect analysis)[J].清华大学学报:自然科学版(Journal of Tsinghua University:Science and Technology), 2002, 42(3): 353-357.
[4] 别朝红, 王秀丽, 王锡凡(Bie Zhaohong, Wang Xiuli, Wang Xifan).复杂配电系统的可靠性评估(Reliability evaluation of complicated distribution systems)[J].西安交通大学(Journal of Xian Jiaotong University), 2000, 34(8): 9-13.
[5] 戴雯霞,吴捷(Dai Wenxia, Wu Jie).基于最小路的配电网可靠性快速评估法(Fast evaluation for distribution network reliability based on minimal path)[J].电力自动化设备(Electric Power Automation Equipment),2002,22(7): 29-31.
[6] Xie Kaigui, Zhou Jiaqi, Billinton R. Reliability evaluation algorithm for complex medium voltage electrical distribution networks based on the shortest path[J].IEE Proceedings: Generation, Transmission and Distribution, 2003, 150 (6): 686-690.
[7] 杨文宇, 余健明, 同向前(Yang Wenyu, Yu Jianming, Tong Xiangqian).基于最小割集的配电系统可靠性评估算法(Reliability assessment algorithm of power distribution system based on minimal cut sets)[J].西安理工大学学报(Journal of Xian University of Technology), 2001, 17(4): 387-391.
[8] Billinton Roy, Wang Peng, Zhang Wei. Reliability assessment of an electric power system using a reliability network equivalent approach[C]∥IEEE WESCANEX Conference on Communications, Power and Computing, Winnipeg, Canada: 1997.
[9] Billinton R, Wang P. Deregulated power system planning using a reliability network equivalent technique[J].IEE Proceedings: Generation, Transmission and Distribution, 1999, 146(1): 25-30.
[10]Wang Peng, Billinton Roy, Geol Lalit. Unreliability cost assessment of an electric power system using reliability network equivalent approaches[J].IEEE Trans on Power Systems, 2002, 17(3): 549-556.
[11]Billinton R, Wang P. Reliability network equivalent approach to distribution system reliability evaluation[J].IEE Proceedings: Generation, Transmission and Distribution, 1998, 145 (2): 149-153.
[12]万国成,任震,田翔,等(Wan Guocheng, Ren Zhen,Tian Xiang,etal).配电网可靠性评估的网络等值法模型研究(Study on model of reliability network equivalent of distribution system reliability evaluation)[J].中国电机工程学报(Proceedings of the CSEE),2003,23(5): 48-52.
[13]Billinton R, Allan R. Reliability Evaluation of Engineering Systems, 2nd Edition[M].New York: Plenum Press, 1992.
[14]Allan R N, Billinton R, Sjarief I,etal.A reliability test system for educational purposes——basic distribution system data and results[J].IEEE Trans on Power Systems, 1991, 6(2): 813-820.
[15]Billinton R, Satish Jonnavithula. Test system for teaching overall power system reliability assessment[J].IEEE Trans on Power Systems, 1996, 11(4): 1670-1676.
ApplicationofMinimum-cutsetandNetwork-equivalentMethodinDistributionSystemReliabilityAnalysis
QI Yan-peng1, ZHANG Yan1, YU Jian-ping2, GUO Zheng2
(1.Department of Electric Engineering, Shanghai Jiaotong University,Shanghai 200240, China;2.Shanghai Municipal Electric Power Co., Shanghai 2000122, China)
A method of minimum-cutset and network-equivalent is introduced to obtain a better result of the reliability evaluation of complex distribution system. The reliability network equivalent method is used to reduce the complex distribution system,and the minimum cutset method is used to enhance the precision and speed of the reliability calculating. The proposed method overcomes the deficiency of the original method such as maintenance and the second-order faults can not be calculated. The results of the RBTS system by using this method examine the validity.
distribution system; minimum-cutset; network-equivalent; reliability analysis; Roy Billinton test system(RBTS)
2009-05-12
2009-12-08
TM711
A
1003-8930(2011)02-0098-07
祁彦鹏(1982-),男,硕士研究生,研究方向为电力系统规划及可靠性。Email:qiyanpeng112233@163.com
张 焰(1958-),女,教授,博士生导师,研究方向为电力系统分析、规划、电力系统可靠性等。Email:zhang_yan@sjtu.edu.cn

