应急电力物资综合调配方案模型设计①

杨旭昕， 刘俊勇， 季宏亮， 郭晓鸣， 贺星棋， 潘 睿

(1.四川大学电气信息学院， 成都 610065； 2.宁夏电力公司， 银川 750001)

应急电力物资综合调配方案模型设计①

杨旭昕1， 刘俊勇1， 季宏亮2， 郭晓鸣1， 贺星棋1， 潘 睿1

(1.四川大学电气信息学院， 成都 610065； 2.宁夏电力公司， 银川 750001)

电力物资的及时有效供应是灾变后电网能快速恢复供电的基本保障，科学合理的电力物资调配能够极大的缩短事故恢复的时间、提高电网运行的安全性及事故的处理效率。根据事故后电力物资需求的特点，利用对称三角模糊数模拟应急活动中的不确定性因素，引入物资供给时间的保障率指标，确定有物资调配时限的最优路径。在此基础上，以最大程度地恢复电网输电能力为目标建立多物资储备点、多物资需求点的电力物资调配方案的数学模型，并用算例验证了方法的有效性及正确性。

物资调配； 三角模糊数； 保障率； 最大输电能力

目前，随着电网互联趋势的逐步深入，电力系统之间的联系日趋紧密，电力系统的安全稳定运行受外界因素的影响程度也日益增强，尤其是近年雪灾、地震等自然灾害造成中国南方地区大量电力设施受损，电力行业的安全连续生产面临着更加严峻的考验。电力作为当今人们生活和工作必不可少的能源，它的中断会给用户和社会造成巨大的影响。相比于电力系统稳定性所引起的电网事故，由外力(如冰灾、地震、台风)所引起的电网事故对电力基础设施的破坏程度更为严重，对其修复对物资的需求量和紧急程度也更高。

物资调配方案的制定受物资储备仓库和物资需求点的地理位置，仓库的物资储备量，恢复供电的时效性等因素制约，应综合考虑多方面的因素。在目前对物资调配方案的研究中，绝大部份只涉及电力抢修的最优路径问题，如文献[1，2]分别利用Dijkstra算法和改进粒子群算法求出最佳电力抢修路径，其目标就是在出发点和目的地之间找到一条最短路径。而对电力物资调配及抢修设备对电网影响程度等方面问题的讨论几乎是空白。

为了有效解决该问题，本文引入管理学中应急管理的理念[3～7]，结合电网运行及物资需求的特点，将电力抢险物资调配问题分解为最优路径、电力设施重要性评价及物资调配三个子问题。通过对称三角模糊数刻画物资运输期间的不确定性因素，建立模糊运输网络模型，搜索物资运输的最高保障率路径。结合实际，在多物资仓库，多物资需求点的条件下，根据各输电线路的恢复对电网输电能力的影响确定物资需求的优先级，建立以综合保障率为目标的应急电力物资调配方案。

1 电力物资需求特点分析

电力系统作为一个连续物资消耗系统，它的正常运行离不开有效的物资保障及供给，结合电力系统自身的特点分析可知灾变后电力系统对电力物资的需求具有以下特点：

1.1 及时性和有效性

由于电网各部分之间电磁联系的紧密性，网络结构的缺陷决定了电网的局部突发事件可能导致在很大范围内都具有极大的危害性，并且蔓延速度很快。电力作为一种公共基础产业，在国民经济和日常生活中具有不可替代的作用。如果不及时有效地采取应对措施，必定会造成电网运行状况的进一步恶化和发展。而对此类事故的处理应建立在充分有效的物资保障基础上，因此，应急电力物资调配的首要目标就是及时性和有效性。

1.2 季节性

电力系统的大部分电力设施处于自然环境中，很容易受到自然灾害(如地震、水灾、风灾、雪灾、冰灾等)的毁坏，这些事故都有鲜明的季节性特点。因此，电力系统对电力物资的需求也具有鲜明的季节特点。

1.3 网络性和复杂性

电力系统因为其特殊性(输电塔、输电线路遍布各个角落)，在灾害发生时对各类电力物资的需求可能不是单点的，同时由于外界不确定性因素的影响，如气候、交通等，导致电力物资的调配往往涉及多专业、多领域、多层面，因此在进行具体的调配时必须对这些因素进行综合考量。

1.4 动态博弈性

由于电力网络在空间分布上的广阔性，因此实际运行中，灾变后电力抢险物资的需求点往往不止一个，由于各个破坏点在电网中的重要程度不同，对物资的需求紧迫性也不尽相同。同时，随着修复进程的推进，各物资需求点的重要性可能也在不断的变化。

2 电力物资综合调配方案模型设计

由上两节分析可知，电力系统对电力物资的调配是一个包含众多约束条件的复杂问题，其中含有很多无法用精确语言描述的不确定性因素。若直接对其进行建模求解，则是一个复杂的非线性多目标问题，求解比较困难。

当前具体电力应急物资调配主要面临三方面问题：一是物资的路径决策问题即确定物资运送的最优路径问题；二是物资需求的优先级决策问题即确定各受损电力设施的最优恢复顺序；三是物资的调配决策问题即选择物资调配点，确定物资调配量的问题。这三个问题既相互联系又有所区别，共同构成完整的应急电力物资的调配方案，见图1。

图1 电力物资的调配方案Fig.1 Power material allocation program

从电力物资的实际调配流程出发，按其阶段性分解为最优路径、物资需求优先级和物资调配三个子问题分别进行研究。对这三个子问题，可分别通过图论、连续潮流法和线性规划进行求解。

3 电力物资调配的最优路径

3.1 数学模型

电力公司在各地设立了各级不同储备规模的电力物资储备仓库，以便在电网发生故障或灾变时能够及时调集物资进行抢修。不防把各个物资仓库、交通枢纽和被破坏的输电线路抽象为节点，而节点之间的连线距离代表两节点间物资运送的时间。

由于电力系统物资需求的季节性和复杂性，根据具体的运输条件只能对运输时间做出一个近似的模糊估计。为了有效地刻画实际中存在的这种时间上的模糊性，本文引入对称三角模糊数来表示这种时间的不确定性。此外，由于电力系统的社会公益性及基础性，通常要求必须在某个时间内恢复电力供应，因此对于电力抢险物资的到达时间也有限制。而由于模糊数本身的数学性质无法与实数时间进行比较，本文引入保障率指标来寻找最优路径，在上述条件下建立电力抢险物资调配最优路径的数学模型。

设S1，S2，…，Sn为当前的n个电力物资储备仓库，D1，D2，…，Dm为m条被破坏的输电线路即电力物资需求点，它们分布在图G(V，E)的节点上，物资储备仓库与物资需求点之间通过交通道路相连。图G中除上述节点外的其余节点代表交通枢纽。对G中的每一条边e对应权值为ω(e)，在模型中代表物资在两个节点之间的运送时间。

设Rij为Si到Dj的所有通路的集合，若P是G中连接任意两点的一条路，路P的权为P中所有边的权之和记为ω(P)：

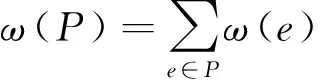
(1)

设t为物资运送限制期，则满足要求的路径集合为A={[P|ω(P)≤t，P∈R}，要在满足要求的路径里寻找最短的一条P0，因此电力物资调配的目标函数为

(2)

在上述模型中，ω(P)为对称三角模糊数，因此路径之间通常无法直接比较，本文通过引入保障率指标来解决这一问题。

定义保障率M(P，t)为路径P的运输时间小于等于限制期t的程度。对保障率进行有效而准确的分析，可以衡量路径承担运输风险的能力。

对任意一个对称三角模糊数

a=[al，am，au]

(3)

可知

(4)

函数图像如图2所示。把区间[al，au]看作是时间的可能范围，把μa(x)看作是时间可能性分布密度，而限制期t为普通实数，可用时间t所截三角形面积(如图2阴影部分)与整个三角形面积的比来定义a≤t的可能度，即模型中的保障率指标。

对时间限制t得出路径P的保障率指标表达式如下[8]：

M(P，t)=

(5)

式中权值ω(P)l，ω(P)m，ω(P)u为[9]

(6)

因此目标函数式(2)可等效为

(7)

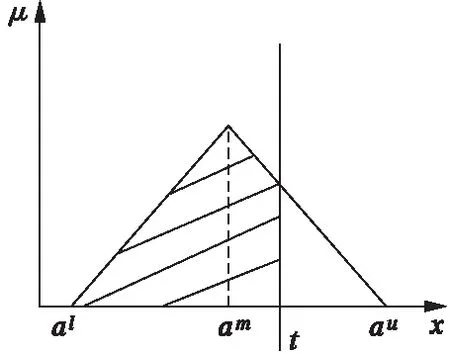
图2 对称三角模糊数的隶属函数Fig.2 Membership function of symmetrictriangular fuzzy number

3.2 模型求解

因路径权值由三角模糊数表示，不能直接运用最短路算法(如Floyd算法、Dijkstra算法)。由文献[10]可知，式(7)可转化为如下等价形式求解。

(8)

式中x0∈[-1，0]

路径P0对应保障率为

(9)

由于式(8)是一个较复杂的非线性路径问题，进一步将这一问题进行转化。

记P(x)：

(10)

P(x)为给定 值时，式(10)的最优解对应的路径，因此问题最终转化为先求x的值，再利用最短路算法，求取最优路径[10,11]。记：

(11)

x的具体求解步骤如下：

①令x=0，若Q(0)≤t，则P(0)为最优路径，否则转②；

②令x=-1，若Q(-1)>t，则P(-1)为最优路径，否则转③；

③令x′=-1，x″=0转④；

④取x=(x′+x″)/2，若|Q(x)-t|<ξ，则P(x)为最优路径，停止。否则，转⑤；

⑤若Q(x)>t，则让x″=x，否则x′=x，转④。

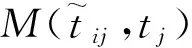
4 物资需求的优先级

由于遭到破坏的电力设施众多，实际情况中物资仓库的物资储量及运输能力有限，必须集中物资优先恢复电网中的重要设备。对电力设备恢复的优先级确定应以能够最大程度增强系统的运行稳定裕度为目标。由于电网线路故障的组合情况很多，故障后电网的运行方式发生变化，并随线路的恢复而改变。本文不考虑电力物资需求的动态博弈性，只讨论电网发生故障后既定的电力物资调配方案，以线路恢复后电网的最大输电能力作为物资调配方案中对线路重要性的评估指标。电网最大输电能力(TTC)是指系统在满足一定的安全稳定约束条件下可以传输的最大功率[12]，以此作为指标可以制定出合理高效的物资调配方案，达到最快最好恢复电网输电能力的目的。

用连续潮流法计算TTC的思想是在给定的发电机节点群和负荷节点群上，在一定系统运行方式下，分别增加送受电功率，然后求解系统潮流方程，并检查是否有线路过载或节点电压越限，重复这一过程直到出现越限为止[13]。此时的送点功率即为当前运行方式下输电网络的最大输电能力。根据这一思想，引进负荷参数 ，并假设有 个负荷节点且负荷的有功无功按比例增长，得到目标函数：

(12)

通过计算恢复不同线路的TTC，以此对线路重要性进行评价，得出物资需求的优先级排序。

5 电力物资调配

5.1 问题描述

通过上述分析可获得从仓库到需求点的最高保障率路径和物资需求的优先级。此外还需确定调用哪些仓库的物资，每个仓库针对不同的物资需求点调运多少物资，才能使其综合效益最高。应急电力物资调配的最终目标是在满足物资需求和限制期的条件下，考虑各物资需求点在受损电网运行中的重要性，使方案能在限制期内完成物资调配的综合保障率最高。

综合考虑运输路径的保障率和线路重要性的影响可能遇到以下问题：线路的优先级别虽然很高，但是通过最优路径计算所有仓库都不能在限制期内满足其物资供应。由于电力物资供应的首要目标为及时性和有效性，在制定应急电力物资调配方案时，对物资运输的优先级还需根据保障率做出调整，剔除所有仓库对其物资运输的保障率均为0的线路(在本文的物资调配方案中不考虑对其的物资运输)，从而形成新的物资运输优先级排序，完成物资调配方案的建立。

5.2 数学模型及求解

完整的物资调配方案是根据建立的物资需求优先级排序结果，依次针对每一个物资需求点建立物资调配方案形成的。若某一优先级别只有单一需求点，则最优方案的做法是：选取保障率最高的仓库参与应急。如果它的全部物资量小于需求量,则再让保障率第二高的仓库参与应急，以此类推,直至满足应急物资的需求。若涉及到某一优先级别有多个物资需求点的情况，则需要找到一个全局的综合保障率来刻画该方案的优劣。对上述单点和多点问题建立统一的数学模型如下：

假设任一可行方案表示为

(13)

定义该方案的综合保障率为

(14)

则最优方案φ*对应目标函数如下：

(15)

此模型是一个有约束条件的线性规划问题，用现有的各类线性规划求解方法很容易求得结果。对每一优先级的物资需求点利用式(15)计算，即可得到完整的物资调配方案。

6 算例分析

6.1 最优路径

如图3所示，该网络为一边权为对称三角模糊数的模糊交通网络。

以IEEE14节点系统为例，假设事故时线路6-13、2-5、6-11、12-13、5-4退出运行，对相应受损设备进行抢修需电力物资的供给才能进行，分别将以上线路和物资仓库抽象为交通网络图中的节点。线路与节点对应关系如表1。物资仓库与节点对应关系如表2。

假设事故后所有物资需求点要求物资在24 h内运达才能满足电力抢险应急要求，用本文的方法搜索从物资仓库到需求点的最优路径及对应保障率(部分结果)如表3所示。

表1 线路节点对应关系表Tab.1 Corresponding relation between nodes and lines

表2 仓库节点对应关系表Tab.2 Corresponding relation between nodes and stores

表3 最优路径及对应保障率Tab.3 Optimal path and guarantee rate

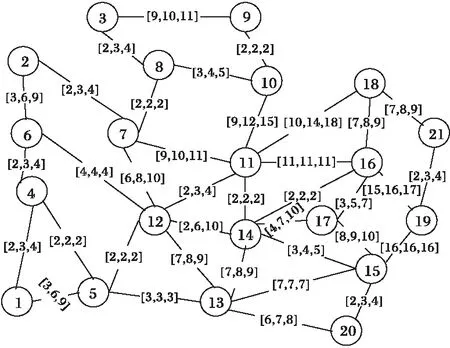
图3 模糊交通网络Fig.3 Fuzzy traffic network

6.2 物资需求优先级

用连续潮流法计算恢复任一线路的最大输电能力，将结果排序如表4所示。

将以上结果结合3.1节的保障率，不考虑综合保障率为0的物资需求点的物资调配，得到如表5所示排序结果。

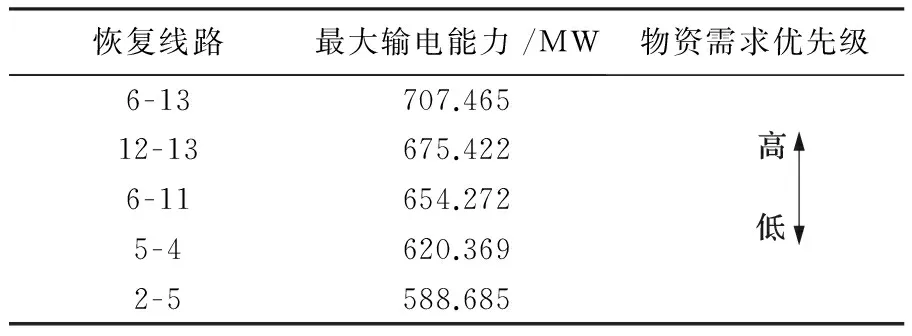
表4 物资需求的优先级排序Tab.4 Priority of material demand

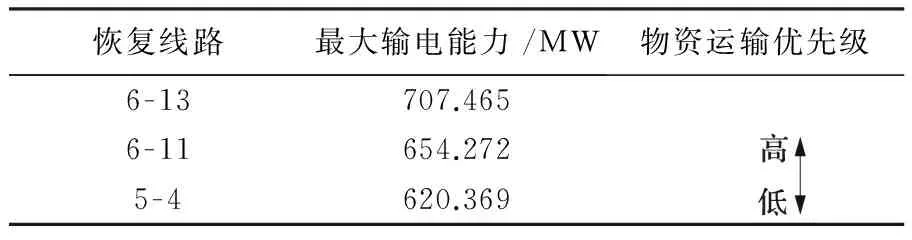
表5 考虑综合保障率物资运输的优先级排序Tab.5 Priority of material transportation based oncomprehensive guarantee rate

6.3 物资综合调配方案

假设物资仓库S1，S2，S3的物资储量分别为90，90，90，故障线路恢复所需物资对应D1，D2，D3，D4，D5分别为40，50，50，50，40。根据表5的运输优先级排序得到物资调配方案如表6所示。

从以下方案可以看出，考虑应急物资调配时，物资供应总量不变的情况下，需有针对的优先恢复重要输电线路。对于某些重要但短时间内并不能满足其物资供应输电线路，无法恢复运行，则不予优先考虑。选择综合保障率较小的调配方案符合实际要求。

表6 物资调配方案Tab.6 Material allocation program

7 结语

针对灾变后应急电力物资的综合调配问题，本文在分析事故后电力系统对电力物资需求特征的基础上，根据输电线路对电网最大输电能力的影响建立了多物资供应点、多物资需求点的电力物资调配模型。通过引入对称三角模糊数描述现实世界的不确定性因素并通过保障率指标对模糊目标的进行转化求解。最后利用线性规划快速得到物资调配方案。由于在变后电力系统的故障情况很多，本文提出的评估线路重要性指标只能在一定程度上反映输电线路恢复对电网的影响，且影响调配方案的因素除了时间，还受成本等其他因素影响。如何在更多复杂情况的影响下建立多目标的应急电力物资调配方案是今后的工作方向。

[1] 叶品勇,都洪基,沈曦(Ye Pinyong,Du Hongji,Sheng Xi).Dijkstra算法在最佳抢修路径计算中的应用(Application of the Dijkstra algorithm in the best repairing path)[J].继电器(Relay)，2006,34(12):39-41，51.

[2] 张铭泉,胥鸣,秦文韬(Zhang Mingquan,Xu Ming,Qin Wentao).基于改进粒子群算法的电力通信网最佳抢修路径问题的研究(Research of the best repair path based on an improved particle swarm optimization in power communication network)[J].科学技术与工程(Science Technology and Engineering),2008,8(22):5990-5995.

[3] Fan Y. Optimal Routing Through Stochastic Networks[D].USA: University of Southern Californian, 2003.

[4] Yu Gang,Yang Jian. On the robust shortest path problem[J].Computers and Operations Research, 1998,25(6):457-568.

[5] 邹志云,宋程,虢向阳(Zou Zhiyun, Song Cheng, Guo Xiangyang).基于灰色理论的应急物流最优路径选择(How to select the optimal emergent logistics route based on grey theory)[J].物流技术(Logistics Technology),2008,27(1):46-48.

[6] Rathi A K, Solanki R S, Church R L. Allocating resources to support a multicommodity flow with time windows[J].Logistics and Transportation Review,1993,28(1):167-188.

[7] Linet Ozdamar, Ediz Ekinci, Beste Kucukyazici. Emergency logistics planning in natural disasters[J].Annals of Operation Research, 2004,129(1):217-245.

[8] 何建敏,刘春林(He Jianmin, Liu Chunlin).限制期条件下应急车辆调度问题的模糊优化方法(Fuzzy programming problem for vehicle dispatch under time restriction)[J].控制与策(Design and Control),2001,16(3):318-321.

[9] 戴更新,达庆利(Dai Gengxin,Da Qingli).多资源组合应急调度问题的研究(The study of combinatorial scheduling problem in emergency systems)[J].系统工程理论与实践(Systems Engineering Theory & Practice),2009,12(9):52-55.

[10]何建敏，刘春林，曹杰,等.应急管理与应用系统一选址、调度与算法[M].北京:科学出版社，2005.

[11]陈大宇,肖峻,王成山(Chen Dayu,Xiao Jun,Wang Chengshan).基于模糊层次分析法的城市电网规划决策综合评判(A Fahp-based Madm method in urban power system planning)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2003,15(4):83-88.

[12]刘盛松,蒋传文,侯志俭(Liu Shengsong,Jiang Chuanwen,Hou Zhijian).基于最优潮流的最大传输能力计算(Optimal power flow based total transfer capability calculation)[J].上海交通大学学报(Journal of Shanghai Jiaotong University),2004,38(8):1233-1237.

[13]刘焕志,李扬,陈霄(Liu Huanzhi,Li Yang,Chen Xiao).基于连续潮流的输电网可用输电能力计算(Availiable transfer capability calculation based on continual power flow for transmission network)[J].电力自动化设备(Electric Power Automation Equipment),2003,23(12):5-9.

DesignofEmergencyPowerMaterialAllocationModel

YANG Xu-xin1， LIU Jun-yong1， JI Hong-liang2， GUO Xiao-ming1，HE Xing-qi1， PAN Rui1

(1.School of Electrical Engineering and Information，Sichuan University，Chengdu 610065， China；2.Ningxia Electric Power Company，Ningxia 750001， China)

The effective and timely supply of power material is the basic guarantee for quickly service restoration after a disaster. Scientific and rational allocation of power material could greatly reduce the time of recovery, and increase the safety of power grid and the efficiency in handling the accident. Triangular fuzzy number was used to simulate the uncertainties in the emergency response activities. Based on the characteristics of demand for power material, the optimal path with time limits is determined by the guarantee rate of time for material supply. And a mathematical model of emergency power material allocation program for multi-material reserves and multi-material needs was established to achieve the goal of maximizing total transfer capability of the grid. Examples proved the efficiency and validity of the proposed approach.

material allocation； triangular fuzzy number； guarantee rate； total transfer capability

2010-01-21

2010-04-06

国家自然科学基金项目(50977059)

TM769；TM73

A

1003-8930(2011)02-0085-07

杨旭昕(1988-)，男，本科，主要从事电力系统稳定与控制方向研究。Email:yangxuxin@gmail.com

刘俊勇(1963-)，男，教授，博士生导师，主要从事电力市场、分布式发电、灵活输电与电力系统可视化等方面的研究。Email:scdxliu@ehdc.com.cn

季宏亮(1970-)，男，高级工程师，工程硕士，主要从事继电保护，自动化方向研究。Email:sck2101@163.com