大传动比减速器动力学建模及分析

王兰

西安航空职业技术学院，陕西 西安

大传动比减速器动力学建模及分析

王兰

西安航空职业技术学院，陕西 西安

重视机械结构系统的动力学问题，研究机械系统在实际工作状态下的受力变化、运动情况及其动态行为，以满足机械结构静、动态特性及低振动、低噪声的要求。因此，有必要对所设计的减速器系统进行扭振动力学分析，找到影响动态特性的薄弱环节，从而为进一步动态结构优化设计、提高减速器的动态性能提供了理论依据。

传动比；动力学；数学模型；扭转；振动

Drive ratio;Dynamics;Mathematical model;torsional;Viberation

机械臂在探测器执行任务中起着决定性的作用，机械臂的各个关节的减速器必须具有较轻的质量，以减轻关节驱动电机的负载，而且应该具有较大的传动比以提高机械臂机械手的控制品质。因此，小体积、大传动比、高转矩、高效率减速器的研制开发已成为减速器产品研究的新课题。本文对所设计的减速器系统进行扭振动力学分析，找到影响动态特性的薄弱环节，从而为进一步动态结构优化设计、提高减速器的动态性能提供了理论依据。

1.系统扭转动力学模型的建立

减速器结构如图1所示,为了分析该传动系统的动态特性，首先需要根据其结构建立动力学模型。根据各种零件动力学作用的不同，可把组成系统的各元件分成两类，即惯性元件和弹性元件。

A.将轴上的齿轮和其他质量较大而直径比较小的零件作为只有惯性而无弹性的惯性元件。

B.计算两刚性圆盘之间所有轴段的扭转刚度和转动惯量，将各轴段的转动惯量迭加到该轴的两惯性元件上，各轴段的扭转刚度转换成一个弹性轴段的扭转刚度，其值应与两惯性元件之间实际轴段的扭转刚度相等。

C.将各轴上的两刚性圆盘和弹性轴段,转换到同一轴线上，构成单一轴线的当量圆盘系统的扭转动力学模型。

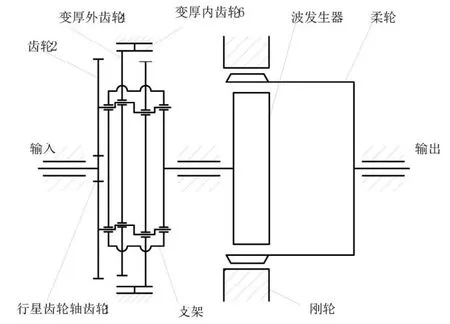
图1 减速器传动系统机构简图

1.1 惯性元件的等效转动惯量

假设输入轴上齿轮的角速度为ω1,外齿轮2，3的自转速度为ωz2、公转速度为ωg2,J’

1表示外齿轮1的转动惯量，J’2表示外齿轮2，3的转动惯量。由于三齿轮表面经过渗碳淬火，弹性变形很小(啮合处的弹性元件可以忽略)，所以相啮合的3个齿轮可合并成一个惯量元件,转换后该等效元件的当量转动惯量为J1。按动能相等原则有

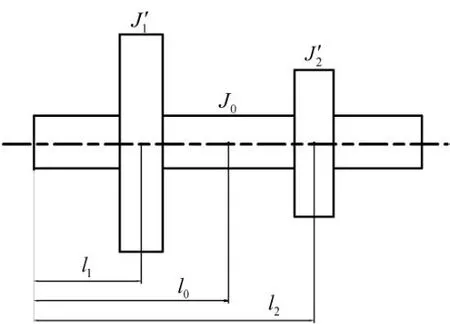
图2 轴的转动惯量分配

设等效分配到惯性元件1上的转动惯量为J01，分配到惯性元件2上的转动惯量为J02,则有所有轴的转动惯量，均可作同样的处理，从而求得系统振动中各单元的转动惯量如表1所示。

1.2 弹性元件扭转刚度的确定

1 )轴的扭转刚度

根据材料力学的理论，轴的扭转刚度为

式中G—为材料的剪切弹性模量；

l—为轴的受扭长度(mm)；

Jp—为轴的极惯性矩(m4)。

利用上述公式，求出各轴段的扭转刚度k1,k2,……,kn，再根据刚度串联公式(8)：

将各轴段的刚度串联起来，从而求得整根轴的扭转刚度k。

2 )轴的等效扭转刚度

弹性元件按转换前后势能相等的原则进行转换,其通用转换公式为

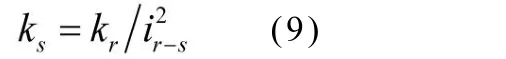
上式为r轴上的弹性元件的扭转刚度kr向s 轴转换后得到的新扭转刚度ks。

假设该轴的弯曲应变能为U1，扭转应变能为U，等效扭转应变能为U，则

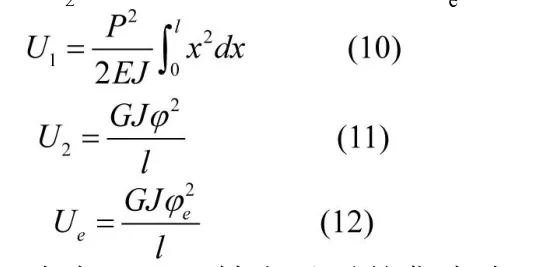
式中P——轴上承受的集中力 ；

J——极惯性矩;

E——拉压弹性模量;

G——剪切弹性模量;

x——轴向长度变量;

ψ——扭转角;

l——轴段长度。

即可得到曲柄轴段的等效扭转刚度为：

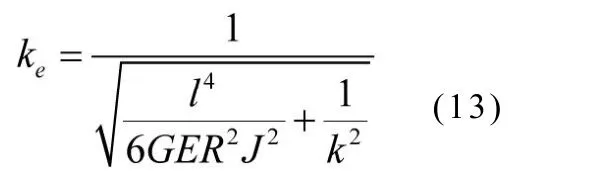
式中 k—只考虑扭转变形时轴段的扭转刚度(N.mm/rad)；

R —曲柄轴中心至输入轴中心的距离，即扭转半径 (mm)。

1.3 轴类零件扭转阻尼的确定

轴类零件的扭转阻尼主要是材料阻尼，根据H.H.Lin和C.Lee等的分析，其扭转阻尼可根据下式进行计算：

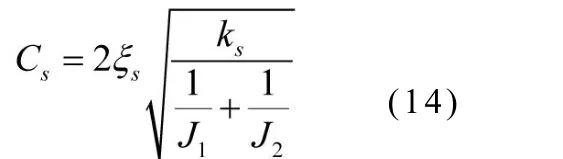
式中ks—轴类零件的扭转刚度 (N.m/rad)；

ξs—轴类零件的扭转阻尼系数，根据D.R.Houser等的实验研究

J1J2—分别为轴类零件两端惯性元件的转动惯量(kg.m2)。

在按照上述公式将各轴的刚度和阻尼转换到输入轴上后,根据该减速器各元件的实际尺寸计算得到表2和表3的数值。

表2 各弹性元件的等效刚度(N.mm/rad)

表3 各弹性元件的等效扭转阻尼(N.mm.s/rad )

2.系统扭转振动数学模型的建立

2.1 扭转系统中惯性元件的数学模型

图3为惯性元件的力学模型,Jj为元件转动惯量, fj为外加激振力矩,两端与相邻元件的连接点分别为 jL和jR,作用于该元件左右两端的扭矩与扭角分别为

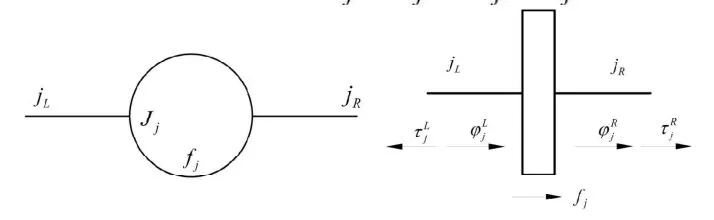
图3 惯性元件的力学模型简图

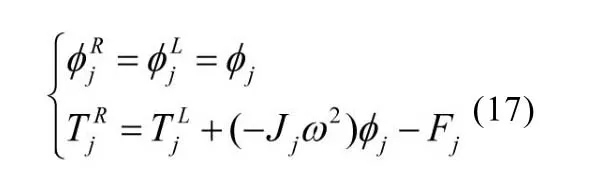
2.2 系统扭振数学模型的建立

图3中所示的谐波传动系统是由十四个二端元件组成,七个惯性元件和七个弹性元件,利用传递矩阵的原理,建立系统的扭振数学模型。将图中十四个元件从左到右依次编号为，则其各个二端元件的数学模型分别为：

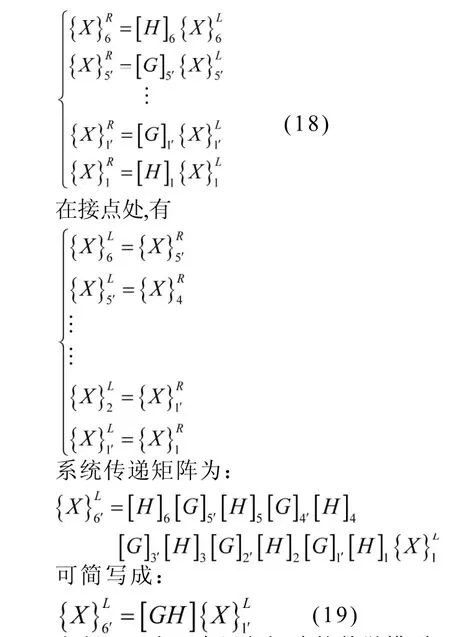
方程(19)为一个累积矩阵的数学模型。用它可以对扭振系统进行计算、分析和评价，也可以进行系统的修改和优化设计。3.扭振动力学分析

利用前面建立起来的减速器系统的动力学模型对减速器系统进行扭振分析。

本文采用数值法编制MATLAB程序对其进行迭代求解，流程图如图4所示。另外，利用该程序还绘制出了减速器系统的振型曲线，如图5所示。由振型曲线图可以看出5～6之间振幅剧增，即此环节最弱,主要影响因素是矩阵H3，所以提高此轴段刚度k3即可。通过适当增大轴的直径或减小其长度可以提高其扭转刚度。本文将轴颈增大2mm后得到新的振型如图6所示。

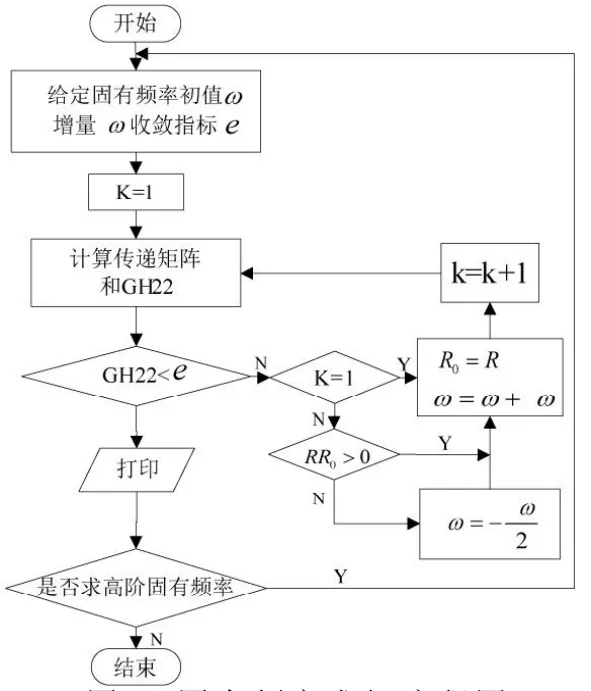
图4 固有频率求解流程图

图6 调整后的振型曲线

4.小结

为了保证减速器具有良好的动态性能必须对减速器进行动力学分析。根据集中参数法将减速器的各个零件简化成相应的惯性元件和弹性元件，建立了减速器系统的动力学模型。同时，根据能量守恒定理将各惯性元件和弹性元件转换到输入轴上，进一步得到了适于用传递矩阵法进行动力学分析的等效动力学模型。在建立起惯性元件和弹性元件动力学数学模型的基础上，利用传递矩阵法建立了减速器系统的动力学数学模型。利用所建立的动力学模型，通过MATLAB编程分析减速器的自由振动，得到了该系统的固有频率和各阶振型等动态特性参数，结果表明，该装置具有良好的动态特性，非常适合用于空间机械臂传动及其他精密机械传动中。

[1]Ueura.Keigi.Slatter. Development of harmonic drive gear for spaceapplications. European Space Mechanisms and Tribology Symposium. Sept.29-Oct.1, 1999:259～264

[2]孙晓军,翁立军,于德洋.固体润滑谐波减速器真空运行性能的试验.机械传动.1998,22(4):22～24

[3]袁茹,纪名刚.航空行星减速器的振动特性分析.航空动力学报.1995, 10(4):395 ～398

[4]Daigill.lee. Development of the composite flex spline for acycloid typeharmonic drive using net shape manufacturing method.Composite Structures.1995, 32:557 ～565

[5]R.malti and A.K.Roy. MINIMUM TOOTH DIFFERENCE IN INTERNAL-EXTERNAL INVOLUTE GEAR PAIR .Mech.Mach.Theory Vol. 31,No. 4,1996 :475～485

[6]周晖，温庆平,张伟文.谐波减速器在空间飞行器中的应用.真空与低温.2004,10(4):187～192

Attention to the dynamics of mechanical structure system to study the mechanical system in the state of the actual work force change, movement and their dynamic behavior to meet the mechanical structure of static and dynamic characteristics and low vibration and low noise requirements. Therefore, it is necessary to the design of the gear torsional vibration analysis system, find the weak link of the dynamic characteristics, dynamic structure for the further optimization of design to improve the dynamic performance of gear to provide a theoretical basis.

10.3969/j.issn.1001-8972.2011.19.051