门式刚架面内振动特性分析的精细传递矩阵法
祝彦艳 朱利 .烟台市建筑设计研究股份有限公司,山东 烟台 64000;.机械工业勘察设计研究院,陕西 西安 70055
门式刚架面内振动特性分析的精细传递矩阵法
祝彦艳1朱利21.烟台市建筑设计研究股份有限公司,山东 烟台 264000;2.机械工业勘察设计研究院,陕西 西安 710055
精细传递矩阵法无需求对微分方程进行求解,只需按照迭代公式进行计算,就可以得到所需要的传递矩阵。本文推导了门式刚架在面内自由振动时的精细传递拒阵。通过实际的计算,证实了该方法是一种具有较高精确度且简便易行的方法。
精细传递矩阵;刚架桥;控制微分方程; 振动
precise transfer matrix method;steel frame;control differential equations;vibration
刚架桥这一类结构的面内自由振动,是横向自由振动和纵向自由振动的耦合。通常在分析时,往往不考虑其纵向振动的影响,这在低阶频率范围内影响尚不大,但在高阶自振频率范围内则有较大的误差。本文提出了门式刚架结构在面内振动时,同时考虑横向振动及纵向振动的传递矩阵及分支处的传递矩阵;本文将精细传递矩阵法[1-2],应用于门式刚架结构的振动特性分析。利用转折处的坐标变换矩阵和分支点处的传递矩阵,满足了位移的协调条件和力的平衡条件,最终将门式刚架结构的动力分析演化成一链式的矩阵相乘过程,从而求得其自振时的各阶频率。
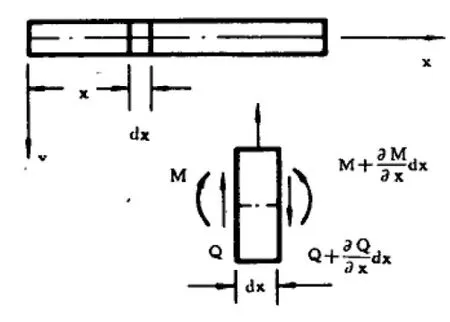
图1 直梁横向自由振动图
1 横向自由振动的传递矩阵
直梁在横向的自由振动如图1所示,其振动微分方程[3]为:

式(3)的一般解为:
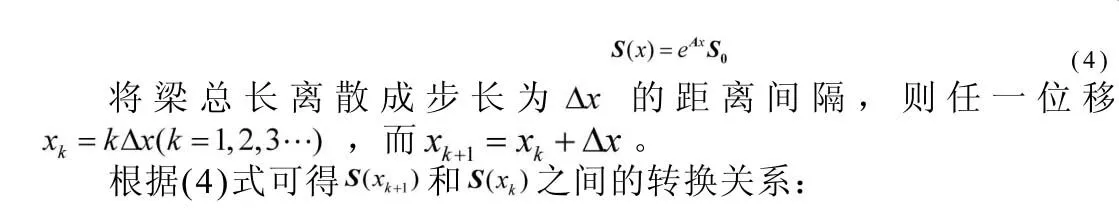

2 纵向自由振动的传递矩阵
直梁在纵向的自由振动如图2所示,其振动微分方程为:

按照(4)~(9)式的步骤计算得到直梁纵向振动的传递矩阵。
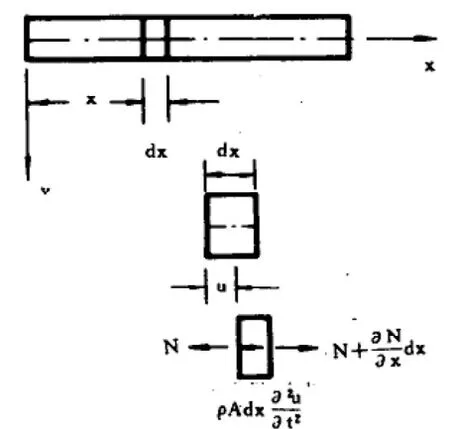
图2

图3 转折处
3 门式刚架面内自由振动的传递矩阵
门式刚架在面内自由振动时,对于任一段杆,其传递矩阵应同时考虑横向和纵向自由振动。将2节和3节所得到横向和纵向自由振动传递矩阵进行组合,即可得到门式刚架面内自由振动的传递矩阵。
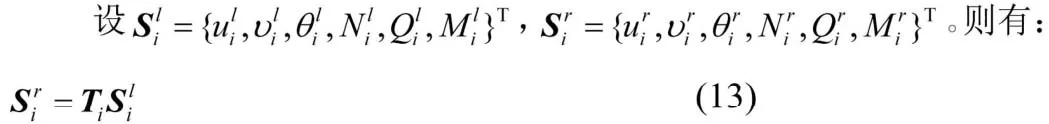
式(13)中的Ti即为门式刚架面内自由振动的传递矩阵
4 转折处的传递矩阵
在转折处如图3所示,左右状态向量存在如下的转换关系:

5 自振频率的求解
各段梁的传递矩阵确定之后,任一段的状态向量可由下式求得:

6 算例分析
算例,某大跨径门式刚架结构的简化模型如图4所示。计算中,以相对值表达取



图4 计算简图
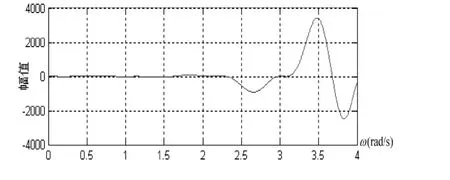
图5 频率函数曲线
7 结语
(1)将指数矩阵精细算法应用于传递矩阵法的求解,能有效控制传递矩阵的精度,可以精确求解结构的自振频率,进而可以分析结构的振动特性等问题。
(2)算例分析证实了本文算法的高精度与高效率。

表1 结构的自振频率
[1]孙建鹏,李青宁.结构地震反应的频域精细传递矩阵法[J].世界地震工程,2009,25(2):140~145.
[2]孙建鹏,李青宁.基于传递矩阵法的曲线桥的振动特性分析
[J].西安建筑科技大学学报(自然版),2009,41(4):518~523.
[3]张荣山.工程振动与控制[M].北京:中国建筑工业出版社,2003
[4]刘庆潭,倪国荣.结构分析中的传递矩阵法[M].北京:中国铁道出版社,1997.
[5]王一凡.直接积分法与精细积分法结合求解结构动力方程[J].工业建筑,2006,36(增)554~566
Precise Transfer Matrix Method for Vibration Characteristics Analysis of The Steel Frame in Plane
Zhu Yanyan1Zhu Li2
1.Yantai Architectural Design Co., Ltd.shan dong yan tai 264000; 2.Xian Li Qun Architectural Engineering Architects,shaan xi xi′an 710055
Precise transfer matrix method is no need to solve the differential equations, just following the iterative formula, the necessary transfer matrix can be get.The transfer matrix on free vibration of a frame in plane and out plane is advanced in this paper.Practical calculations show that this method is accurate,simple and practicable.
TU375
A
10.3969/j.issn.1001-8972.2011.22.070

