运用CAE工具进行两阶段结构优化设计

汪冬生 南京地下工程建筑设计院有限公司，江苏 南京 210029

运用CAE工具进行两阶段结构优化设计

汪冬生 南京地下工程建筑设计院有限公司，江苏 南京 210029

本文利用CAE工具，对一受集中荷载作用的矩形板依次进行拓扑优化与尺寸优化的计算与分析，最后得到给定条件下的合理结构。研究结果表明，拓扑优化与尺寸优化相结合的结构系统优化设计方法，是解决具有较少目标的结构优化问题的一种有效方法。

CAE技术；工程结构；拓扑优化；尺寸优化；有效性

CAE Technique; Engineering Structure; Shape Optimization;Size Optimization;Validity

1 前言

CAE(Computer Aided Engineering的缩写), 是指用计算机辅助求解分析复杂工程和产品的结构力学性能，以及优化结构性能等，它是计算机技术发展的基础上出现的一门新兴学科。采用CAE技术，即使对复杂的工程分析也无须作很多简化，并且计算速度快、进度高。常见的工程分析包括对质量、体积、强度、应力、变形、稳定等的计算分析，以及对产品的运动精度、动静态特征等的性能分析。

本文利用CAE工具，结合已有的研究成果，对一典型构件进行了两阶段优化设计，最后得到在满足各项设计要求下的最优化设计方案。

2 两阶段结构优化设计方法

2.1 结构拓扑优化

拓扑优化即形状优化，有时也称为外形优化。从理论上讲,广义的结构拓扑优化是指: 确定结构单元、节点及内部边界的空间连接方式。拓扑优化的目标是寻找承受单载荷或多载荷的物体的最佳材料分配方案。与传统的优化设计不同的是，拓扑优化不需要给出参数和优化变量的定义。目标函数、状态变量和设计变量都是预定义好了的。设计者只需要给出结构的参数（材料特性、模型、载荷等）和要省去的材料百分比，以及一定约束条件（如位移、频率、稳定性等）。很明显，拓扑优化的目标是得到物体的最佳形状。

目前，拓扑、布局优化技术有多种，比较有效的方法有基于连续体结构拓扑优化的均匀化方法[1]、渐近结构拓扑优化法[2]等，后者是通过将无效或低效的材料一步步去掉，结构将逐渐趋于优化。该方法采用已有的有限元分析软件，通过迭代过程在计算机上实现，通用性很好。渐近结构拓扑优化法不仅可以解决形状和拓扑优化问题，还可以实现应力、位移（刚度）、振动频率、响应、临界压力等优化。

目前，已有不少国内外软件能够处理结构拓扑优化问题（由于拓扑优化的理论尚不成熟，故都还处于发展阶段）。需要注意的是，基于CAE技术的拓扑优化的结果对网格划分密度十分敏感。一般来说，很细的网格可以产生“清晰”的拓扑结果，而较粗的网格会生成“混乱”的结果。但是，较大的有限元模型收敛需要更多的时间。

2.2 结构尺寸优化

为了使设计方案满足使用上的各项要求，对结构需施加一定的约束，一般分为显式约束和隐式约束。显式约束是直接施加于一个或几个设计变量的限制。而隐式约束即状态变量，是间接施加于设计变量的限制。基于CAE技术的隐式约束需要通过求解有限元方程间接得到。约束条件在设计空间中构成一个曲面，它代表等式满足约束条件的设计点的轨迹。对于不同点的设计方案，将具有不同的目标函数值。在该阶段的设计中，需要设计者找出使目标函数值最小的点[2]。

对于已知的给定参数，求出满足全部约束条件并使目标函数取极小值的设计变量。用数学方式表示，就是极小化目标函数 W(x)

满足约束条件的设计中，关于应力和位移的约束条件，通常都是设计变量的非线性函数[1]。

这是一个数学规划问题。

结构尺寸优化作为一种数学方法，通常是利用对解析函数求极值的方法来达到寻求最优值的目的。基于数值分析技术的CAE方法，显然不可能对我们的目标得到一个解析函数，CAE计算所求得的结果只是一个数值。然而，样条插值技术又使CAE中的优化成为可能，多个数值点可以利用插值技术形成一条连续的可用函数表达的曲线或曲面，如此便回到了数学意义上的极值优化技术上来。样条插值方法当然是种近似方法，通常不可能得到目标函数的准确曲面，但利用上次计算的结果再次插值得到一个新的曲面，相邻两次得到的曲面的距离会越来越近，当它们的距离小到一定程度时，可以认为此时的曲面可以代表目标曲面。那么，该曲面的最小值，便可以认为是目标最优值。以上就是CAE方法中的优化处理过程。一个典型的CAE优化过程通常需要经过以下的步骤来完成：

(1)参数化建立几何模型：利用CAE软件的参数化建模功能把将要参与优化的数据（设计变量）定义为模型参数，为以后软件修正模型提供可能。

(2)求解运算：对结构的参数化模型进行加载与求解（用数值方法求解选定的数学模型）。

(3)提取并指定状态变量和目标函数。

(4)后处理：把状态变量（约束条件）和目标函数（优化目标）提取出来供处理。

3 算例与讨论

3.1 拓扑优化

问题是求图1所示的结构在集中荷载F作用下的拓扑优化设计。以渐近拓扑优化理论[3]为基础，基于应力水平的材料删除。图2显示了删除率[3]RR为30%时的拓扑优化结果。（这里将设计区城分成 四节点等尺寸的平面应力单元，板的厚度取为50mm，并假设F＝1MPa，L＝1m，H＝2.4m,弹性模量E＝ 100Gpa，泊松比ν＝0.3，比重ρ＝7.85× 103Kg/m3）。

本问题拓扑优化的目标函数是结构总体积，通过对优化前后的数据比较发现结构的总体积从优化前的2.4降低到0.389，如图3所示，降低量是原设计的85%。另外，拓扑的最终结果显示H＝2L[3]。

3.2 尺寸优化

条件约束是当荷载P作用于结构时，各杆中的最大拉应力不得超过137MPa，最大压应力不得大于100Mpa，且不大于纵向屈曲时的临界应力σcr和局部屈服应力σs；载荷作用点允许的最大竖向位移uy。下面求该构件（见图4）的最小重量。

图4 结构计算及尺寸示意图

根据分析问题的性质，选择杆的直径D1、D2和管壁厚t为设计变量(必须是正值,如图4所示)；状态变量为杆内的（轴向）应力值、压杆稳定条件以及集中载荷处的竖向位移，目标函数为构件的最小重量。

综上所述，该问题的优化数学模型为：

优化结果见下表。

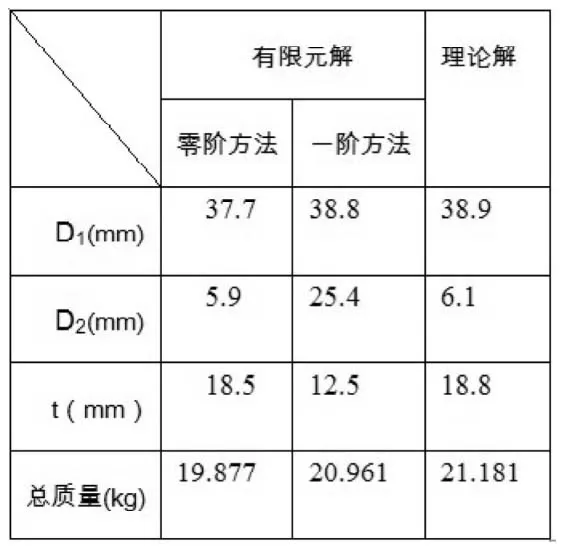
表1 尺寸优化结果表

利用MATLAB优化组件[4]得到的理论解为D1=38.9, D2=6.1和t=18.8。设计变量D1、D2、t和目标函数的大小随迭代过程的变化规律分别如图5、6所示。

综上可得到以下结论：当管子的尺寸分别为D1=37.7, D2=5.9和t=18.5时，整个结构的重量最轻(此时总质量为19. 877kg),也得到了最佳设计。

在静载荷工况作用下，构件拓扑优化问题中很难处理欧拉失稳问题[5]，如还需要考虑基频约束，问题会变得较复杂。为此，本例在尺寸设计阶段才具体考虑稳定性等问题，这样使问题容易解决。

4 结论

本文利用CAE工具对一典型结构进行了两阶段优化设计。优化结果显示，将拓扑优化与尺寸优化相结合的系统优化设计方法，对解决具有较少目标的优化问题，是一种行之有效的新尝试，具有很好的应用前景。对于应用两阶段优化方法处理多目标的优化问题，今后还需要进一步研究。

[1]XIA Li – juan, Study on Topology Optimum Design of Engineering Structures[J], China. Journal of Ship Mechanics. Dec, 2002～. 6594

[2]朱伯芳.有限单元法原理与应用[M].北京：水利电力出版社.1979.394～400

[3]荣见华,郑健龙,徐飞鸿编著.结构动力修改及优化设计[M].北京:机械工业出版社.2002. 249～251

[4]飞思科技产品研发中心编著.辅助优化计算与设计[M].北京:电子工业出版社.2003.1. 91～93

[5]童卫华,徐斌,姜节胜.具有频率约束的结构拓扑优化新方法[J].西北工业大学学报.2002.1. 14～19

Two Stage Construction Optimization Design Method Useing on the CAE Technique

By utilizing the CAE tool, this paper optimizes a typical construction combining the already research results which have been, finally getting the optimum design of construction under satisfying the variously requests. Combining topology optimization with size optimization together, here gets a kind of valid new trial of the construction optimization on the CAE Technique. But for many targets problems, it still need the further research.

Wang Dongsheng Nanjing Underground Engineering & Architectural Design In，stNitaunreji nCgO J.,iLaTnDg su 210029China

10.3969/j.issn.1001-8972.2011.11.061

汪冬生（1978-），男，国家一级注册结构工程师、土木（岩土）工程师。主要从事结构、岩土方面的设计和研究工作。