液态结构与性质关系Ⅰ
——Mg熔体的运动黏度及与熔体微观结构的关系*
弭光宝李培杰Охапкин А ВКонстантинова Н ЮСабирзянов А АПопель П С
1)(清华大学新材料国际研发中心,北京 100084)2)(Научно-исследовательскый центр Расплав ,Уральский Государственный Педагогический Университет,Екатеринбург 620017,Россия)(2010年8月25日收到;2010年9月16日收到修改稿)
液态结构与性质关系Ⅰ
——Mg熔体的运动黏度及与熔体微观结构的关系*
弭光宝1)李培杰1)Охапкин А В2)Константинова Н Ю2)Сабирзянов А А2)Попель П С2)
1)(清华大学新材料国际研发中心,北京 100084)2)(Научно-исследовательскый центр Расплав ,Уральский Государственный Педагогический Университет,Екатеринбург 620017,Россия)(2010年8月25日收到;2010年9月16日收到修改稿)
采用坩埚扭摆振动法测量 Mg熔体的运动黏度,得到935—1190 K温度区间高精度的黏度-温度关系曲线 v(T),发现升温和降温过程中Mg熔体的黏度随温度变化呈指数规律单调递增(减),没有发生异常变化和滞后现象.同时,利用液态结构中原子集团演变行为的物理模型,计算得出该温度区间Mg熔体的主要结构信息参数——原子集团尺寸-温度关系曲线d(T);通过对实验和计算数据的综合分析,发现Mg熔体的运动黏度和原子集团尺寸均为温度的单值函数,且二者之间存在线性的函数关系v(d),即v=v0+K·d(T).该函数关系揭示了Mg熔体微观结构的黏度变化特性,为计算金属熔体的运动黏度及深入认识其微观本质提供了新途径.
金属熔体,结构与黏度相关性,原子集团演变,线性关系
PACS:66.20.Ej,66.20.Cy,61.25.Mv,36.40.-c
1.引 言
液态作为物质存在的一种基本形态,与固体、气体相比,液体具有其特殊的结构、性质及其变化规律,同时液体还是晶态和非晶态固体材料的母体,因此液体特别是高温熔体的微观结构及物理性质的研究十分重要[1].
液态金属的黏滞特性研究一直是人们倍感兴趣的课题,一方面它是熔体结构的最敏感物性参数,能够间接反映液态结构的变化,另一方面它能够揭示出液、固态之间相互联系的信息,如预测晶体组织性能[2]、判断非晶形成能力[3,4]等,同时它还是重要的铸造工艺参数[5].目前,有关熔体黏度及结构方 面 的 研 究 已 见 很 多 报 道[1,2,6—9],如 Al,Sn,Sb,Si,Fe等,据黏度随温度的变化特性,基本上可分为三类:1)黏度-温度关系曲线连续变化,即黏度随温度单调变化(减小或增大),多见于简单金属;2)黏度-温度关系曲线不连续变化,即存在异常变化(突变或跳跃),常见于半金属;3)升温和降温过程的黏度-温度关系曲线不重合,即黏度不是温度的单值函数,存在滞后现象.
然而,固态下具有hcp结构的镁的熔体黏度随温度的变化特性是否属于上述第一类情况、熔体的微观结构如何变化等问题的系统研究尚未见报道.这与当前固态条件下镁及合金的组织性能控制及镁工业的发展极不平衡,其主要原因是镁熔体高温的强烈氧化和高的蒸汽压(如1100 K,1个大气压下镁蒸汽压为铝的1.1×107倍[10])使黏度的精确测量十分困难,现有文献中的零散数据基本上源于理论计算或经验公式间接得到[10—12].
此外,仅从黏度-温度关系曲线的异常变化(突变或跳跃)研究金属熔体的微观结构是不完备的,黏度随着温度连续变化的微观本质是什么,二者之间是否存在函数关系?这些问题尚不十分清楚,文献报道也未给出明确的一致性回答.例如,对于Al熔体,有的学者认为黏度在670和750℃发生异常变化是熔体表面的氧化膜形成和破裂所致[13,14],文献[15]用熔体中有序度较高的结构单元相对数量的突变来解释黏度在1050—1250℃区间的异常变化,有的则认为熔体结构发生了类似固体多晶型转变的“多形性变化”[16,17];对于 Sn 熔体,一些学者对比研究了高纯度和工业用 Sn,测量结果表明,前者升温和降温过程的黏度-温度关系曲线重合,即没有发生滞后现象,后者则存在滞后性,当工业用Sn熔体过滤后滞后现象消失,他们认为熔体中存在的不溶杂质是产生滞后本质原因[18],文献[19]则认为黏度分别在 400和800℃发生异常变化,并综合DTA-TG分析结果作出熔体结构发生两次变化的结论;等等.可见,金属熔体的黏度与温度及液态结构之间的关系有待于进一步研究.
鉴于上述,本文精确测量镁熔体的黏度与温度的关系,同时结合前期的理论研究工作[20,21],尝试探索镁熔体的黏度与微观结构之间的内在联系.
2.实验方法
采用坩埚扭摆振动法对935—1190 K温度区间镁熔体的黏度进行测量.黏度测试装置的主体工作部分如图1所示,主要由悬挂系统、加热器以及数据测量系统等组成.测量时,在线圈中通入电流,产生的磁场使悬挂系统开始做扭摆运动,达一定角度后,线圈停止通电,即去掉外力矩,在内摩擦力作用下,系统开始作阻尼扭摆运动,由于悬挂系统扭摆的对数衰减率、周期与熔体黏度保持一定的关系,于是便可通过系统对数衰减率、周期的测算得到运动黏度.

坩埚扭摆的对数衰减率、周期与运动黏度的关系由 Швидковский 公式给出[22]2π;v为运动黏度;M为液体试样的质量;K为悬挂系统的转动惯量;R为坩埚半径;H为液体试样在坩埚中的高度;a,b,c为系统参数;δ为装入熔体的坩埚扭摆的对数衰减率;δ0为空坩埚扭摆的对数衰减率;τ为装入熔体坩埚的扭摆周期;τ0为空坩埚的扭摆周期.
用高纯镁(99.999%)作为实验材料,试样尺寸为Φ14 mm×21 mm.为避免镁熔体的氧化和蒸发对黏度测量产生影响,熔体完全被保护,且蒸发质量小于0.1 g,主要采取以下操作:1)粗磨、细磨试样表面;2)用丙酮清洗试样、坩埚等表面;3)采用带滑动

图1 黏度测试装置的主体工作部分示意图 1悬挂系统,2反光镜,3悬挂系统的容器(向内依次为带螺旋盖的不锈钢坩埚、石墨坩埚、镁熔体),4双线加热器,5数据采集系统,6激光器,7产生磁场的线圈,8水冷系统,9热电偶
式中,盖的石墨坩埚装载试样(镁熔化后石墨盖紧贴熔体表面),然后将石墨坩埚装入带螺旋盖的不锈钢坩埚,再将其装入悬挂系统的容器;4)悬挂系统所在的腔体中采用高纯氦气(99.9995%)保护,即开启抽真空装置,抽真空后充入氦气,然后再抽真空(真空压力表控制),重复四次抽真空操作后,最终腔体中通入压强约为101 kPa的氦气进行保护.
实验过程中,以8 K/min的速度将液态金属试样加热至预先设定温度进行对数衰减率、周期等参数测算(利用图1中数据采集系统5的光电二极管探测).对数衰减率通过关系式 lntn=δ·n+lnt0(t0为悬挂系统扭摆达到一定角度后,激光第一次通过系统5中两个黑色孔的时间;tn为激光第n次通过5中两黑色孔的时间)获得,如图2所示;扭摆周期为激光两次通过5中白色孔的时间.升温和降温过程中,每间隔约30 K测量一次参数,每个温度重复测量5次参数(测量时间约为20 min),每次测量的参数包括30组数据,然后取其平均值进行黏度计算,进一步提高了实验精度.
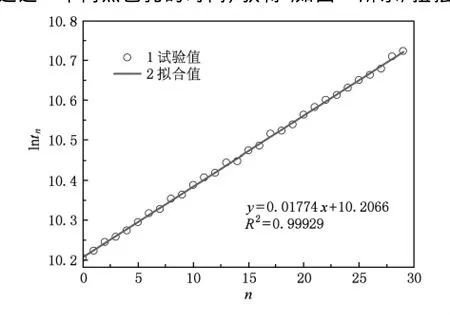
图2 对数衰减率与测量参数之间的关系
从(1)式可知,黏度值的确定是一个间接测量过程,它依赖于多个直接测定参数,即 ν=f(К,М,R,σ,δ,δ0,τ,τ0),因此采用下面公式进行评价测得黏度的相对误差[23,24],即
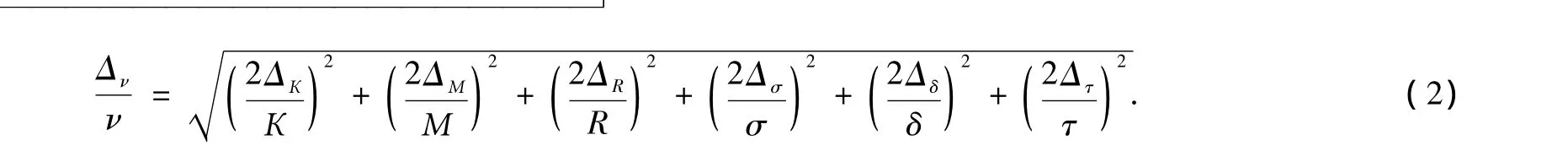
从直接测量及处理后的试验数据中,可以得到:ΔМ/М,Δτ/τ,Δδ/δ,ΔR/R 和 Δσ/σ 分 别 小 于0.05% ,0.03% ,0.05% ,0.01% 和 0.06% ,ΔК/К 按照文献[23]的方法进行取值.于是,据(2)式确定了黏度计算值的相对误差,即升温和降温过程中黏度的相对误差均低于2.2%.
3.结果与分析
图3所示为935—1190 K温度区间镁熔体的黏度-温度关系曲线v(T).从图3中试验值1,2可以看出,在所测量温度区间,镁熔体黏度随温度升高(降低)而逐渐减小(增大),没有发生异常变化;比较升温和降温过程的黏度值发现:在同一温度下,熔体黏度的最大偏差小于2.0%,这说明在允许的误差范围内,升温和降温过程的黏度-温度关系曲线相重合,没有产生滞后现象.
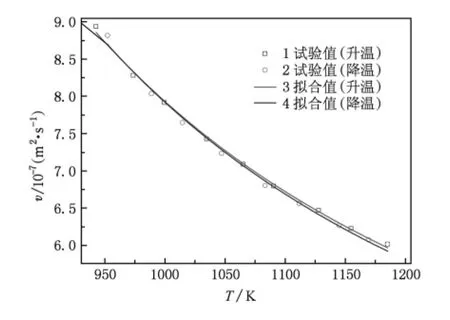
图3 镁熔体黏度-温度关系曲线v(T)
通过试验数据的非线性回归可以得到升温和降温过程的黏度-温度关系拟合曲线 v(T),如图3中曲线3,4所示,黏度随温度变化关系如下:


式中,vH,vC分别为升温和降温过程的运动黏度(m2/s);T为绝对温度(K).
从(3),(4)式中可以看出,镁熔体的黏度随温度的变化规律呈指数关系,且很好地符合Arrhenius方程式[25]
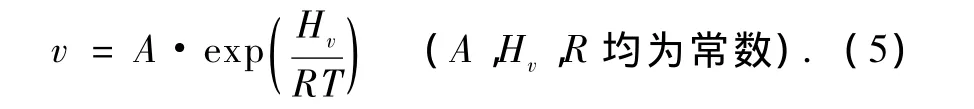
将升温和降温过程测得的黏度视为其中一个过程的试验值进行综合分析,可以得到关系式

比较(3),(4)和(6)式可知,常数的相对差值均小于3.5%,这说明在允许的误差范围镁熔体的黏度是温度的单值函数,即在所测量温度区间,镁熔体黏度的温度变化特性可用(6)式表示.表1是据(6)式计算得到的黏度值与文献数据(包括计算外推值)的比较,综合二者结果的相对误差,可见文献中的零散数据与本试验相应温度的黏度值相符合.

表1 试验数据拟合值与文献数据的比较
由于黏度本质上反映的是熔体中微观粒子间的相互作用,所以黏度随温度的单调性变化体现了熔体微观结构的规律性变化.根据金属熔体结构的微观不均匀性理论[2,27,28],熔化后的金属熔体由带有低能量原子的类晶体原子集团(平均尺寸为 2—5 nm,存在时间约为 10-7—10-8s)和含有高能量激活原子的失稳区域构成.统计意义上,随着温度的升高,熔体中类晶体原子集团的平均尺寸逐渐减小,失稳区域的激活原子浓度逐渐增大[21].Швидковский 等[18]通过研究纯锡和含有杂质的工业纯锡熔体的黏度得出,在压力一定的条件下,熔体中包含在类晶体原子集团内部的原子浓度(数量)仅是温度一个参数的函数;Sklyarchuk等[9]通过研究铝及其合金熔体黏度、密度等物性认为,价电子参与了类晶体原子集团内部价键的形成,当熔体中添加异类元素时,形成的原子集团及其相互作用存在差异,如原子集团由结合力较强的原子构成时,它的存在时间大于由结合力较弱原子构成的集团,这些原子集团是黏性流动的独立单元.在相同温度下,经电脉冲处理的铝熔体的黏度测量及DSC分析结果也证明了这一点[29],黏度的增大是熔体有序化提升、原子集团尺度增大的宏观反映.可见,随着温度升高,原子集团内部及其与周围失稳区域内激活原子之间的相互作用大为减弱,二者之间原子的交换频率增强,从而导致原子集团内包含的近程有序原子的相对浓度减小(失稳区域内原子浓度相对增大),宏观上表现为黏度的降低.
4.讨 论
由上述结果分析可知,宏观上镁熔体黏度随温度的连续变化反映了熔体微观结构的演变规律,即黏度的温度变化特性与原子集团、激活原子浓度等微观结构参数之间存在相互联系.
4.1.液态结构中原子集团的演变行为
据金属熔体结构信息的计算模型[20,21],原子集团的演变行为可以利用激活原子相对浓度CA,原子集团的平均尺寸d及其内部包含的近程有序原子数nij等结构信息参数描述,
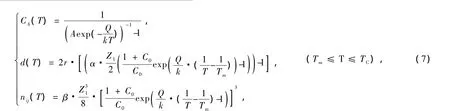
即式中,A为振动熵项;k为玻尔兹曼常数;α为几何形状因子,0(α≤1;Z1为金属熔化前的配位数;r为原子集团中原子间距离;Q为激活能;C0为熔点处激活原子的相对浓度;Tm为熔点温度;TC为熔体从液态到气态转变过程中第一次发生结构转变(原子集团失稳)的温度.
从(7)式可以看出,随着温度的升高,CA逐渐增加、R逐渐减小和nij逐渐减少,即类晶体原子集团内的原子浓度逐渐减小,熔体的有序度不断下降.
将铝的热物理性参数及基本结构参数[30,31]代入(7)式,得到铝熔体中原子集团的平均尺寸随温度变化的关系式
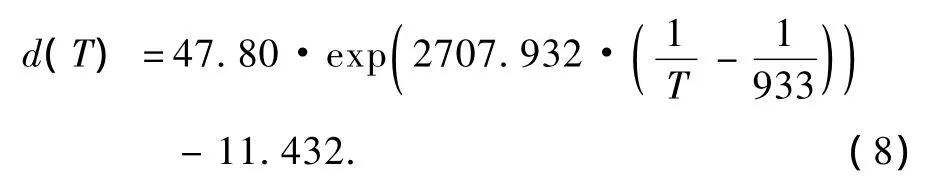
于是,据(8)式计算得出铝熔体中原子集团平均尺寸的变化情况,如图4(a)所示.其中,部分温度所对应的原子集团尺寸已被离心法或X衍射实验测量[32,33],鉴于 X 射线衍射实验得到的相关半径rc表示的是原子集团尺寸的下限值[34],所以可以认为理论计算结果与试验值相符合,这为液态结构中原子集团尺寸计算模型提供了直接的验证.
同理,将镁的热物理性参数及基本结构参数[30,31]代入(7)式,可以得到镁熔体中原子集团的平均尺寸随温度变化的关系式

据(9)式计算得出935—1190 K温度区间镁熔体中原子集团的演变行为,如图4(b)所示,原子集团的平均尺寸随温度升高(降低)而不断减小(增大).

图4 铝、镁熔体原子集团尺寸-温度关系曲线d(T) (a)铝熔体;(b)镁熔体
4.2.黏度与原子集团尺寸的关系
图5是镁熔体黏度与原子集团尺寸之间的关系曲线v(d).从图5中试验值1,2可以看出,升温和降温过程中的黏度随原子集团尺寸的增大近似分布在一条直线上,即熔体黏度随原子集团尺寸的增大而呈线性增加,可见黏度随温度的规律性变化反映了熔体中原子集团的演变行为.
通过拟合镁熔体黏度的试验值(图5中1,2)和原子集团尺寸的理论计算值,可以得到二者之间的函数关系式,即

从(10),(11)式可以看出,镁熔体的黏度 v与原子集团的平均尺寸d之间存在一一对应关系,即黏度随温度的变化规律呈线性关系,可归纳为下面通式:
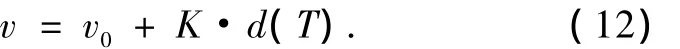
式中,v0,K均为常数;d(T)为原子集团的平均直径(nm);T为绝对温度(K).
同样地,将升温和降温测得的黏度视为其中一个过程的试验值,可以得到关系式

比较(10),(11)和(13)式可知,常数的相对偏差均在3.5%以内,这说明在允许的误差范围镁熔体的黏度是熔体主要微观结构信息——原子集团平均尺寸的单值函数,即镁熔体微观结构的黏度变化特性可用(13)式表示.
(13)式定量描述了镁熔体的宏观黏度与微观结构信息之间的对应关系,综合(7)和(13)式即可以得到液相线以上至TC温度的镁熔体的运动黏度.这为计算镁熔体黏度及深入认识其微观本质计算提供了新的途径.由于熔体黏度与原子集团的平均尺寸均为温度的单值函数,所以该线性函数关系的揭示同时为金属熔体结构信息的计算模型提供了间接验证.

图5 镁熔体黏度-原子集团尺寸的关系曲线v(d)
5.结 论
本文采用坩埚扭摆振动法精确测量了935—1190 K温度区间升温和降温过程的镁熔体的运动黏度,其相对误差低于2.2%;随着温度的升高(或降低),黏度呈指数规律下降(或升高),没有发生异常变化,且很好地符合 Arrhenius关系;比较升温和降温过程的黏度值,发现二者的黏度-温度关系曲线相重合,没有产生滞后现象.同时,利用金属熔体结构信息的计算模型研究了液相线以上不高温度区间的铝熔体结构信息的变化,计算结果与已有试验值相符合,进而研究了935—1190 K温度区间的镁熔体中原子集团的演变行为,随着温度的升高(或降低),原子集团尺寸逐渐减小(或增大).通过实验和理论计算数据分析发现,镁熔体的黏度与原子集团尺寸之间存在线性的函数关系,即v=v0+K· d(T),该线性关系定量描述了镁熔体的宏观黏度与微观结构信息之间的对应关系,为深入认识金属熔体黏度的微观本质提供了新思路.
致谢作者感谢中国科学院物理研究所王强老师在黏度测量精度方面提出的宝贵意见.
[1] Wang Q,Lu K Q,Li Y X 2001 Chinese Science Bulletin 46 1431
[2] Baum B A,Hassin G A,Tyagunov G V 1984 Liquid Steel(Moscow:Metallurgical Industry Press)p6(in Russian)
[3] Angell C A 1995 Science 267 1924
[4] Geng H R,Sun J C,Yang Z X,Wang R,Ji L L 2006 Acta Phys.Sin.55 1320(in Chinese)[耿浩然、孙春静、杨中喜、王 瑞、吉蕾蕾 2006物理学报 55 1320]
[5] Li Y X 2005 Principle of material processing(Beijing:Tsinghua University Press)(in Chinese)[李言祥 2005材料加工原理(北京:清华大学出版社)]
[6] Iida T,Rodarick I L 1993 The Properties of Liquid Metal(Ox-Ford:Clavendon Press)p148
[7] Assael M J,Kakosimos K,R Banish M 2006 J.Phys.Chem.Ref.Data 35 285
[8] Zhang W,Liu C C,Wang H Y,Xu Y S,Shi Y Q 2008 Acta Phys.Sin.57 3875(in Chinese)[张 雯、刘彩池、王海云、徐岳生、石义情 2008物理学报 57 3875]
[9] Sklyarchuk V,Plevachuk Yu,Yakymovych A 2009 Int.J.Thermophys 30 1400
[10] Samsonov G V 1976 Handbook of elemental nature-the first part:physical nature(Moscow:Metallurgy Press)P235(in Russian)[11] Cmitls K R 1980 Metal manual(Moscow:Metallurgy Press)P335(in Russian)
[12] Regel A R,Glazov V M 1980 Physical property of electron melt(Moscow:Science press)P13(in Russian)
[13] Iouns W R P,Bartlett W L 1952 J.Inst.Met.81 145
[14] Alsenchiyev P P 1982 Iron 5 14
[15] Qin J Y,Bian X F,Wang W M,Sliusarenko S I 1998 Acta Phys.Sin.57 3875(in Chinese)[秦敬玉、边秀房、王伟民、Sliusarenko S I 1998物理学报 47 438]
[16] Poole P H,Grande T,Angell C A,McMillan P F 1997 Science 275 322
[17] Reichert H,Klein O,Dosch H,Denk M,Honkimaeki V,Lippmann T,Reiterk G 2000 Nature 408 839
[18] Shvidkovskii E G,Goriaga G I 1956 Journal of Moscow State University 6 33(in Russian)
[19] Yang Z X,Geng H R,Tao Z D,Sun C J 2004 Journal of atomic and molecular physics 21 663(in Chinese)[杨中喜、耿浩然、陶珍东、孙春静2004原子与分子物理学报21 663]
[20] Mi G B,Li P J,He L J 2010 Sci.China Phys.Mech.Astron 53 1571
[21] Mi G B,Li P J,He L J 2010 Sci.China Phys.Mech.Astron 53 1823
[22] Shvidkovskii E G 1955 Some problems in the viscosity of molten metals(Moscow:Gostekhizdat)p83(in Russian)
[23] Bazin Yu A,Zamrtin V M,Hasiipov Ya A 1985 Trans Higher Educ-Ferrous Metall 5 28(in Russian)
[24] Glazov V M,Vobst M,Timoshinko V I 1989 Research methods for the nature of liquid metals and semiconductors(Moscow:Metallurgy Press)p245(in Russian)
[25] Chhabra R P,Seth D K 1990 Z.Metallkde 81 264
[26] Kolobnev I F,Krimov V V,Polianskii A P 1957 Caster manualshaped castings of aluminium and magnesium alloys(Moscow:MASHGR)p5(in Russian)
[27] Li P J 1994 Ph D Dissertation(Harbin:Harbin Institute of Technology)p64—72(in Chinese)[李培杰1994博士学位论文(哈尔滨:哈尔滨工业大学)第64—72页]
[28] Skrebcov A M 2009 Trans Higher Educ-Ferrous Metall 2 28(in Russian)
[29] Qi J G 2006 Ph D Dissertation(Beijing:University of Science&Technology Beijing)(in Chinese)[齐锦刚2006博士学位论文 (北京:北京科技大学)]
[30] Zhang R L 1993 EmpiricalElectron Theory ofSolidsand Molecules(Jilin:Jilin Science and Technology Press)(in Chinese)[张瑞林1993固体与分子经验电子理论 (长春:吉林科学技术出版社)]
[31] Dean J A 1999 Lange’s Handbook of Chemistry(15th Ed.)(New York:McGraw-Hill)P6.124
[32] Levin E S,Geld P V,Yakubchik V P 1975 Acta Metall Sin.USSR Acad Sci.5 80(in Russian)
[33] Roik A S,Samsonnikov A V,Kazimirov V P 2006 Metal 3 24(in Russian)
[34] Byharenko V V,Chen S Sh,Ilinskii A G 1991 Metal Physics 1992(in Russian)
PACS:66.20.Ej,66.20.Cy,61.25.Mv,36.40.-c
Relationship between liquid structure and propertyⅠ—Kinematic viscosity of magnesium melt and its relationship with the microstructure*
Mi Guang-Bao1)Li Pei-Jie1)Ohapkin A V2)Konstantinova N Yu2)Sabirzianov A A2)Popel P S2)
1)(National Center of Novel Materials for International Research,Tsinghua University,Beijing 100084,China)2)(Research Center Melt ,Ural State Pedagogical University,26 Cosmonavtovst,Ekaterinburg 620017,Russia)(Received 25 August 2010;revised manuscript received 16 September 2010)
The method of crucible rotating oscillation damping was employed to measure the kinematic viscosity of magnesium melt and the curve of viscosity v versus temperature T from 935 K to 1190 K was obtained.It is exponential increase(decrease)law of viscosity with the temperature during heating and cooling process;Besides,based on the physical model for evolution behavior of atomic cluster in liquid structure,the main structural information of magnesium melt in this temperature interval—the curve of size d of atomic cluster versus temperature T was obtained;By analyzing the experimental and calculated data,it is found that both kinematic viscosity and size of atomic cluster of magnesium melt are monodrome function of the temperature and the relation between them is linear function,i.e.,v=v0+K·d(T).This relation reveals the change characteristic of viscosity for magnesium melt microstructure,which presents a new way for calculating kinematic viscosity of metal melt and understanding the micro-nature deeply.
metal melt,correlation between structure and viscosity,evolution of atomic clusters,linear relationship
*国家重点基础研究发展计划(批准号:2007CB613702)和国际科技合作项目(批准号:2007DFC50090)资助的课题.
E-mail:mgb07@mails.tsinghua.edu.cn
*Project supported by the National Basic Research Program of China(Grant No.2007CB613702)and International Cooperation Program in Science and Technology(Grant No.2007DFC50090).
E-mail:mgb07@mails.tsinghua.edu.cn

