一个八阶收敛的修正牛顿法

许长勇，肖志华，沈栩竹

（云南大学 数学与统计学院，云南 昆明 650091）

非线性方程的数值解法一直都是非线性科学的一个重要课题。经典牛顿迭代法（CN[1]）是非线性方程求根的基本方法，二阶收敛到单根。牛顿法因收敛速度快而得到广泛应用，也备受学者的重视，近年来很多文献中提出各种修正的牛顿法。Chun提出四阶收敛到单根的两步修正牛顿法（MCN4[2]）；通过对四阶收敛的算法增加一步迭代，Chun和Ham提出六阶收敛的修正牛顿法（MCN6[3]），Kou、Wang和Li提出七阶收敛的修正牛顿法（MCN7[4]）。在此基础上，本文运用导数和均差的性质，提出一个新的八阶收敛的修正牛顿法。

1 算法构造

为方便表述，首先给出一些相关预备知识。

定义1[1]设迭代过程

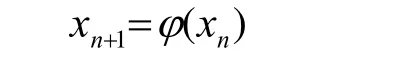
收敛于方程

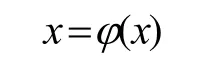
的根*x，如果迭代误差

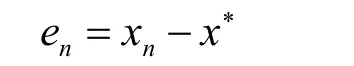
当n→∞时成立下列渐进关系式

称该迭代过程是p阶收敛的，称

为误差方程。

定义2[4]称 p1/d为算法的效能指数，其中p表示迭代算法的收敛阶，d表示每步迭代所需要的计算。

定义3[5]称

为函数 f(x)关于点x0，x1的一阶均差。

为函数 f(x)的二阶均差。

一般地，称

为函数 f(x)的k阶均差。

特别地，

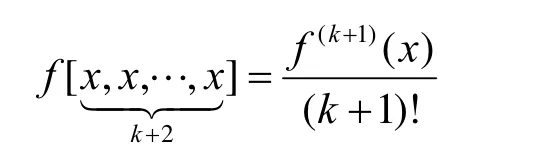
下面构造一个新的八阶收敛的修正牛顿法。

将 f(x)在yn处作泰勒展开，可得：

令 x= zn，可得：

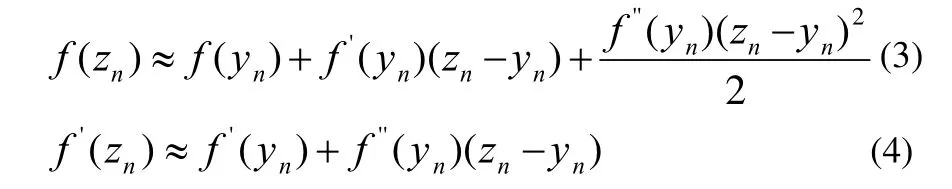
由(3)得：

将(5)代入(4)，可得：

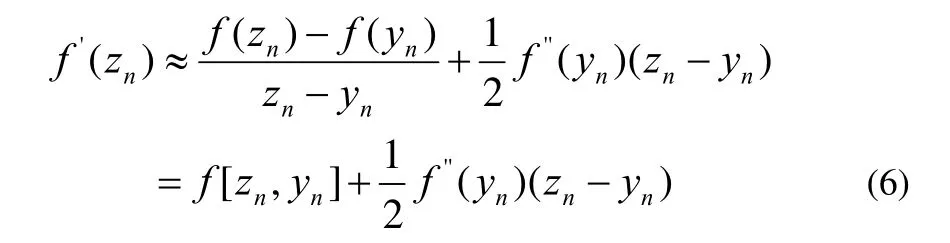
为避免计算二阶导数，考虑如下近似关系：

将(7)代入(6)，可得：

即得到一个新的算法（MCN8）：

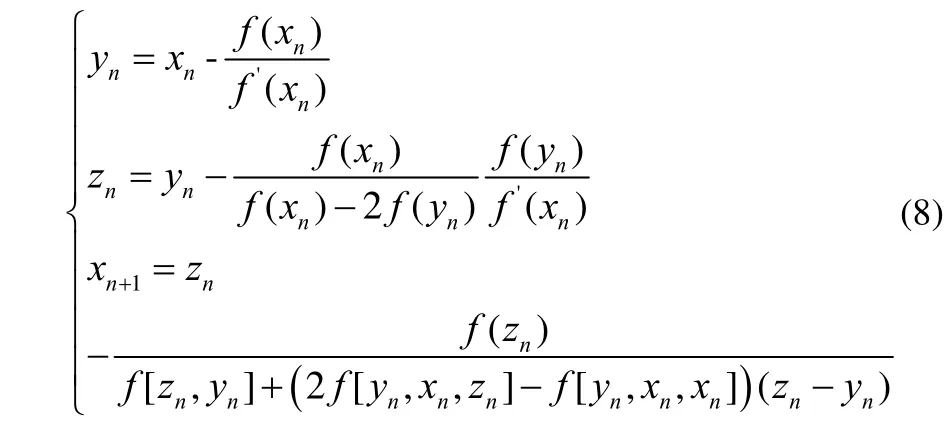
2 收敛性分析

定理1设ξ是充分光滑函数

证明不妨设

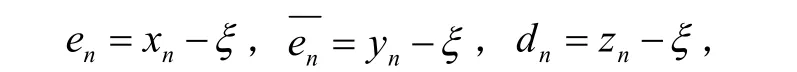
并记

将 f ( xn)，f'(xn)和 f ( yn)在ξ处作泰勒展开，并考虑 f(ξ)=0，可得

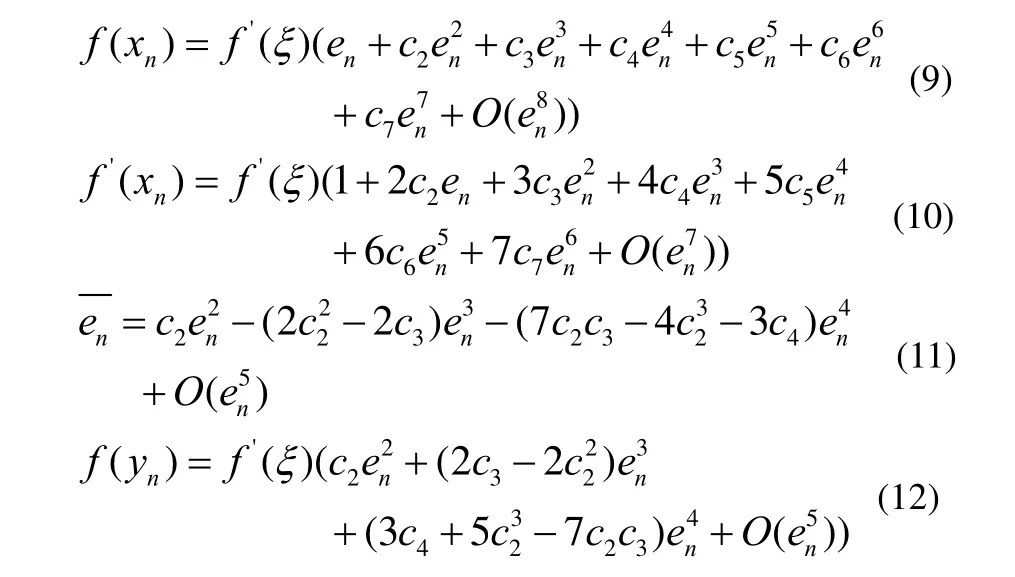
由(9)-(12)得：

从而

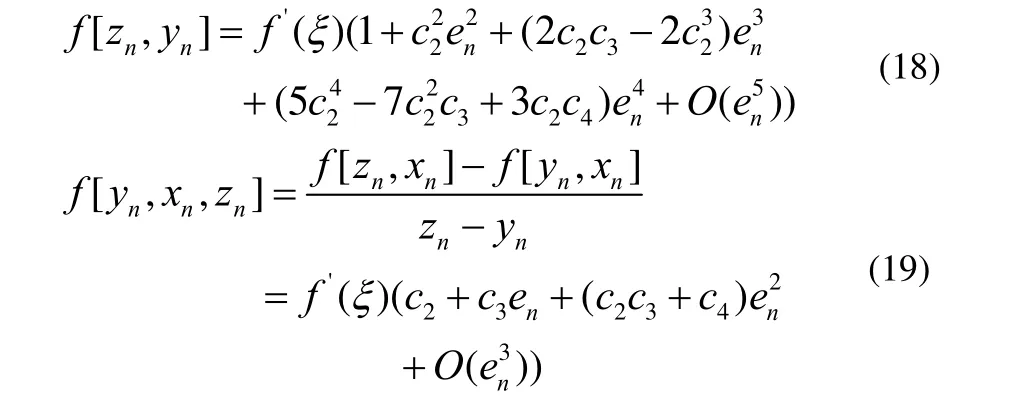
由(15)-(19)得：

即证得由迭代格式(8)所得的序列{ xn}是八阶收敛的。

注衡量一个迭代算法优劣除了考察收敛阶外，还要考察其算法的效能指数。本文算法（MCN8）的效能指数为，显然高于

3 数值试验

为检验本文算法（MCN8）的效率，分别用CN，MCN6，MCN7和MCN8来解下列常用的测试函数方程[3,4]：

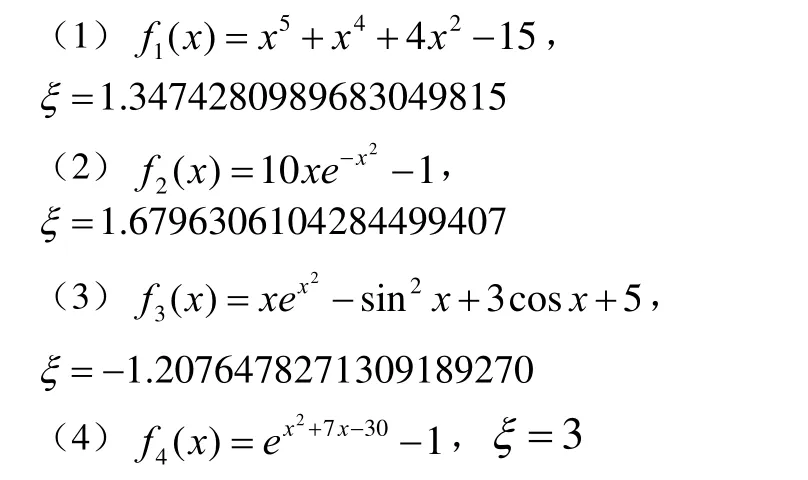
从初始值x0开始迭代，用经过同等函数计算个数（TNFE）运算后的值作为标准，来说明新算法的有效性。所有结果都是在Matlab 7.0的环境下操作，计算结果如表1所示。

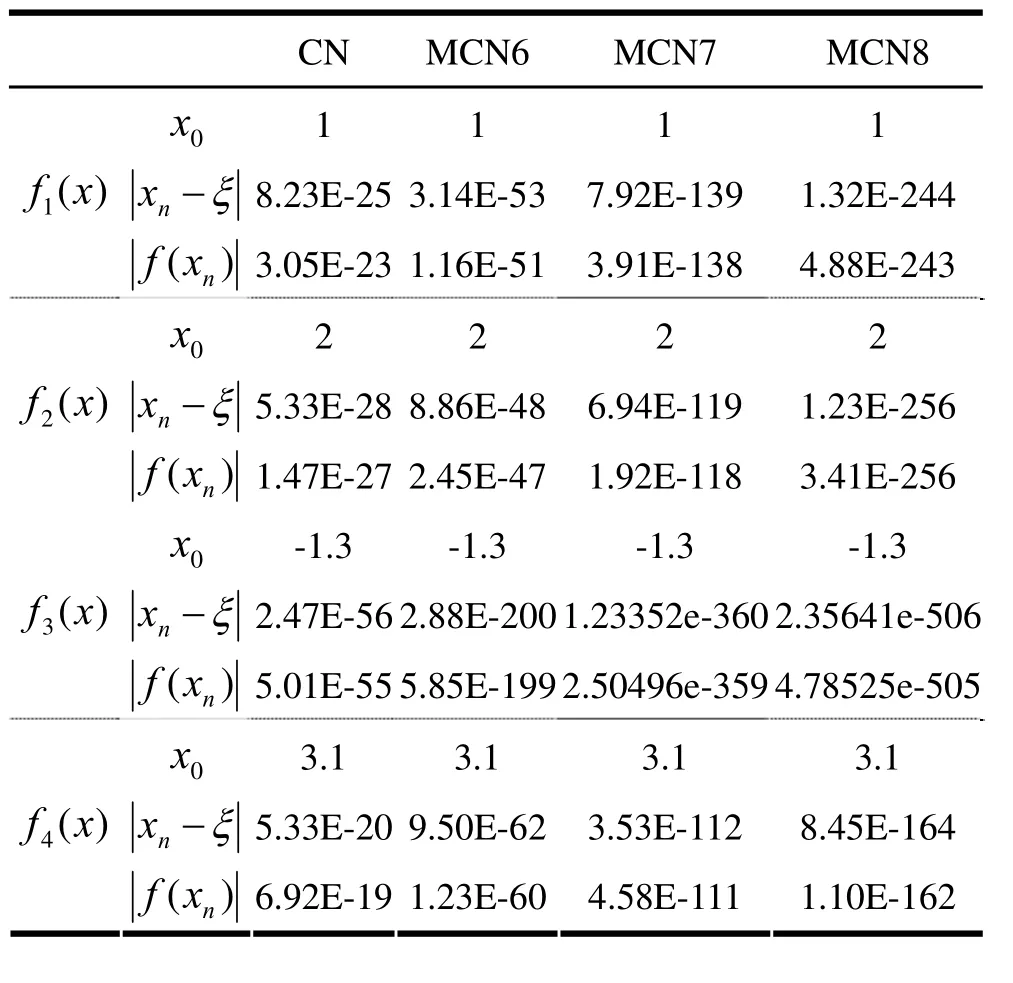
表1 不同迭代法的比较表（函数计算个数总和均为12）

由数值试验可见，新算法（MCN8）具有收敛速度快，精确效果好的特点，故较其他算法具有一定的优越性。

注 在数值试验中，MCN6为文献[3]的式(12)在选取

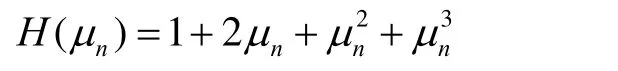
的情况下所得到的算法；MCN7为文献[4]的式(8)在选取α =1的情况下所得到的算法。

4 结论

提出了一个新的八阶收敛的修正牛顿法，理论分析和数值试验表明新算法是一种较优的求解非线性方程的方法。