灾害气候下交通枢纽滞留旅客转移模型研究

沈 洋，罗正军

（南京航空航天大学 经济与管理学院，南京 210016）

灾害气候下交通枢纽滞留旅客转移模型研究

沈 洋，罗正军

（南京航空航天大学 经济与管理学院，南京 210016）

文章针对灾害气候中各重要交通枢纽有大面积人群滞留的情况，采用贝叶斯网络和影响图作为建模工具，研究和设计了滞留旅客转移决策过程模型，为进一步研究滞留旅客在各个交通枢纽的分布和转移规律，进而为政府应急管理决策提供建议建立了理论基础。

应急管理；旅客滞留；旅客转移；建模；贝叶斯网络；影响图

0 引言

近年来，我国不断发生一些非常规突发事件，对社会安定和居民生活造成了严重的影响。如2003年的SARS事件、2008年春南方雪灾及2008年的汶川地震、2010年玉树地震等。新的形势要求政府在新时期提高应急管理水平，从而能够在非常规突发事件发生时进行迅速且科学的决策。因此，建立起非常规突发事件中各种问题的合理研究模型具有重要的意义。

国内外学者对政府应急管理做出了大量研究。这些研究主要集中在应急资源布局问题、警力部署问题、资源评估问题、人员撤离问题、应急预案及应急反应模式等方面[1-5]。对突发事件造成交通受阻时，旅客在交通枢纽的滞留和转移问题尚未见报道。另外，目前文献中对应急管理的研究多以非线性规划等宏观方式进行，不可避免地忽略了一些或许是重要的影响因素。本文针对非常规突发事件（如雪灾）中各重要交通枢纽（汽车站、火车站、机场等）有大面积人群滞留的情况，以滞留旅客个体为研究对象，采用贝叶斯网络和影响图描述旅客在不确定环境下的决策过程，研究和设计了旅客滞留和转移决策过程微观模型，为进一步研究滞留旅客在群体中的涌现行为（如在各个交通枢纽的分布和转移规律等），进而为政府应急管理决策提供建议建立了理论基础。

1 问题描述

设某城市的交通运输系统如图1所示，其中节点1、2、3分别代表汽车站、火车站和飞机场，节点I表示旅客的输入，节点O表示旅客的输出，即旅客离开该交通系统，到达目的地（或放弃出行）。

按照旅客对时间和费用的不同承受能力可以将其划分为A、B、C三类，其中A类人群以农民工为代表，他们比较注重经济成本，而对时间成本要求不高，表现出比较偏好于汽车、火车这两类交通工具的特性；而C类人群是商务人士，他们往往更看重时间成本，相对来说对经济成本不太敏感，相应更偏好于飞机这种交通工具；B类人群则为其他人群。

下文所述的模型试图从微观的角度，对旅客根据所接收的环境信息进行转移决策的动态过程进行建模。

2 旅客转移决策模型

2.1 滞留旅客转移决策模型的贝叶斯网络和影响图

贝叶斯网络可被用于对不确定环境建模，同时，它也能反映出模型中存在因果关系事件的相互影响[6,7]。对不确定环境建模的目的往往是需要将所建立的模型用于决策过程，本文采用影响图来描述旅客在灾害气候下进行运输节点转移决策的模型，如图2所示。

旅客在运输节点间转移决策的影响图由一个决策节点Move，一个效用节点U和一个包含5个事件的贝叶斯网络组成。在这里，可以将贝叶斯网络理解为旅客在不确定的天气条件下对自己进行某个转移决策后的可能等待时间和花费转移成本的思考过程。本文模型贝叶斯网络中各事件的含义与取值如表1所示。

表中，tnormal,tdelay,tcancle分别为班次正常时滞留时间，班次延误时滞留时间和班次取消时滞留时间，其值由公式（1）计算得出：

图2 旅客运输节点转移决策影响图

表1 贝叶斯网络中各节点的含义与取值

式中，tmin为一较小常数，nahead为在排队队列中该旅客之前的旅客人数，可由该旅客所乘班次之前的尚未发出班次数目换算得出，为简化计算，取nahead=n/2,n为所在节点旅客总数，v为该节点最大运力，tlimit为一较大常数，表示旅客所能承受的滞留时间上限。当旅客转移到新的节点时需付出购新票成本，而且此时如果系统未发出旅客原先班次取消信息，则旅客还需付出退票成本，值得注意的是，这里的取消信息是指系统明确发出的班次取消通告，而不是旅客根据贝叶斯网络得到的班次取消概率。crefund，c分别为退票成本和购新票成本，λ≥1，为临时购票系数（表示旅客在转移到其他节点时可能无法以原价购票），crefund，c，λ均为常数。贝叶斯网络中的有向线段表示事件之间的因果关系，如图1中天气的恶化将可能导致交通节点的关闭和班次的延误，班次的延误或或取消又可能导致滞留时间增长。在图1中，除天气事件发生的概率P(W)为自然概率外，其余事件发生的概率均为其父事件（因果关系的源端）的条件概率，如节点状态事件的概率应由式P（SNW)计算，而班次状态事件的概率则应由式P(SRSN,W)计算得出。在仿真计算时，根据预先设定好的一系列条件概率表（Conditional probability table,CPT）来计算相关事件的发生概率。需要指出的是，若有证据表明某事件已经发生，即某个事件节点不再有不确定性时，则该节点之前的因果关系不再发挥作用。例如，在计算滞留事件时，若已发布某班次的延误信息，则天气和交通节点状态不再影响计算结果。下面描述旅客在影响图作用下的转移决策过程。

2.2 旅客的转移决策过程

本节着重解释以上节模型为基础的旅客的转移决策过程。设各项自然概率及条件概率均已知，则旅客的决策过程可描述为以下步骤。当旅客评估决策方案由m0转移至m时：

(1)由天气情况自然概率P(m)(W)及相关CPT求节点状态概率 P(m)(SN)。

根据贝叶斯概率基本原理，有：

(2)由天气情况自然概率P(m)(W)，步骤1求出的节点状态概率P(m)(SN)及相关CPT求班次状态概率P(m)(SR)与步骤1类似，有：

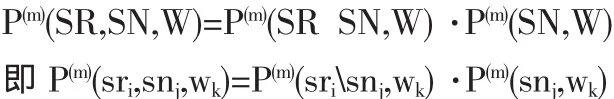
(3)由步骤2求出的P(m)(SR)，转移决策m求滞留时间和转移成本的期望效用

tlimit表示该类型旅客所能承受的时间上限。而：

上式中Ncancel为该旅客班次取消通告标识，Ncancel=true表示系统已发布该旅客所乘班次取消通告。

(4)由成本效用与时间效用的相对权重w求出总效用U的期望值

(5)在进行决策选择时，舍弃效用小于0的方案，并根据剩余方案的效用期望值计算转移概率，计算公式见式(9)

式中E(i)(U)＞0。若任一方案的效用均小于0，则用户将放弃出行，离开系统。

3 算例分析

设各条件概率如表2～4所示。

各节点初始人数、运力、人数估计比例、新购票成本和退票成本等参数见表4。

表中δ为节点人数估计比例。旅客在班次延误的状态下进行转移决策需要根据节点人数评估滞留时间时，当前节点的人数是可以获得的，但其他节点的人数在信息不对称的环境下旅客无法获知，此时旅客根据δ估计出其他节点的人数，作为评价滞留时间的依据。例如，当3号节点人数为40人时，则认为1号节点和2号节点的人数分别为80人和120人。表中3号节点短途新购票成本为∞，表示短途旅客不可能转移至机场。

不同类型旅客的类型参数见表5。

表中各符号含义见第3节。

下面假设有一处于节点2的B类型长途旅客，该旅客对天气情况的判断见表6，且各节点均未发布任何取消通告，则根据第3小节，该旅客决策过程如下：

表2 交通节点状态条件概率表

表3 班次状态条件概率表

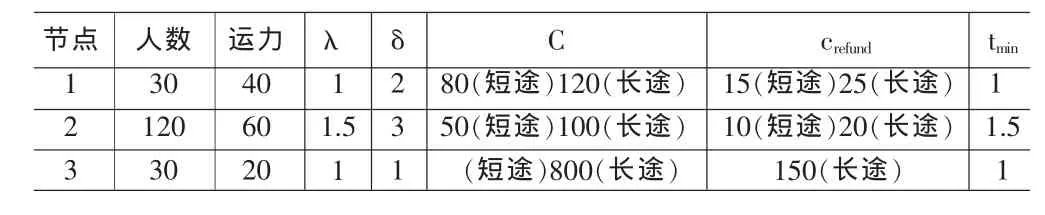
表4 各节点相关参数表

(1)根据式(2)及表(2,6)，可计算出各节点的 P(SN)如表 7所示。

(2)根据式（3）及表（6，7），计算各节点的 P(SR)，结果如表8所示。

(3)根据式(4~6)及表(4,8)，可求出该旅客转移至各节点的效用值。

若旅客无法得知其他节点的人数信息，由于该旅客处于节点2，则2号节点当前人数n2=120为已知，其他节点由人数估计比例δ计算得出，即n1=120*2/3=80，n3=120*1/3=40，那么对该旅客而言：

表5 旅客类型参数表

表6 天气情况的自然概率

表7 节点状态概率

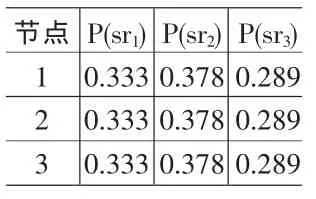
表8 班次状态概率

即该旅客将有更大的可能选择留在2号节点。

但若能及时将各节点的状态告知所有旅客，则可将各节点人数均视作已知信息，那么：

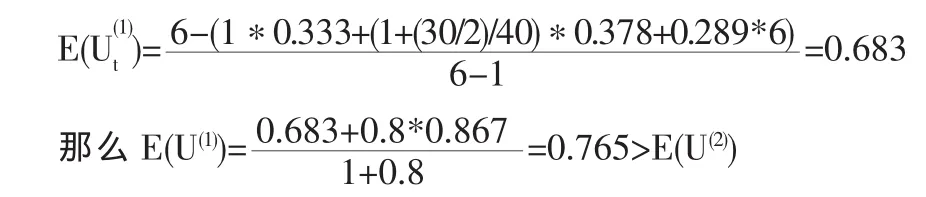
则旅客将有更大的可能选择转移到节点1。

4 结论和展望

本文建立了灾害气候下交通枢纽滞留旅客转移决策过程模型，为进一步研究滞留旅客的动态分布规律建立了理论基础，并通过算例得到以下结论：

（1）使用贝叶斯网络和影响图进行旅客转移问题建模是恰当的，该方法能较好地刻画旅客在不确定性环境中的决策过程。

（2）班次状态、其他交通枢纽滞留旅客人数等信息的及时公布将会对旅客转移决策带来影响。

在后续工作中，作者将开展以下工作：

（1）使用Repast作为仿真环境，建立起该问题的多主体仿真环境，研究滞留旅客的分布和转移规律，进而为政府在相应情况下的应急管理提供决策建议。

（2）研究旅客主体在转移决策过程中受群体的影响和心理变化，在仿真模型中描述旅客主体之间的交互。

（3）研究在本问题中旅客的排队规律，更有效地在模型中描述旅客的等待过程及等待过程本身对转移决策的影响。

[1]ReVelle C.S.,Eiselt H.A.Location Analysis:a Synthesis and Survey[J].European Journal of Operational Research,2005,165(1).

[2]Sherali H.D.,Subramanian S.Opportunity Cost-based Models for traffic Incident Response Problems[J].Journal of Transportation Engineering,1999,125(3).

[3]Barbarosog姚lu G.,Arda Y.A Two-stage Stochastic Programming Framework for Transportation Planning in Disaster Response[J].Operational Research Society,2004,(55).

[4]缪成,许维胜,吴启迪.大规模应急救援物资运输模型的构建与求解[J].系统工程,2006,(11).

[5]杨继君,吴启迪,程艳等.面向非常规突发事件的应急资源合作博弈调度[J].系统工程,2008,(9).

[6]Jensen F.V.An Introduction to Bayesian Networks[M].London,UK:University College London Press,1996.

[7]Howard R.A.,Matheson J.E.Influence Diagrams[J].Decision Analysis,2005,2(3).

(责任编辑/亦 民)

O231

A

1002-6487(2011)03-0045-03

国家自然科学基金资助项目（90924022）

沈 洋(1973-)，男，四川成都人，博士，讲师，研究方向：复杂系统，最优化算法。