隐性知识网络传播行为模型构建及仿真

曹 征，孙 虹

（1.中南大学 公共卫生学院，长沙 410078；2.中南大学 湘雅医院，长沙 410008）

隐性知识网络传播行为模型构建及仿真

曹 征1，孙 虹2

（1.中南大学 公共卫生学院，长沙 410078；2.中南大学 湘雅医院，长沙 410008）

隐性知识一般通过工作经验、技艺、组织文化等方式在工作人员的头脑中留有深刻的印象，并通过工作人员在工作中的实践而得以表现。隐性知识的传播网络存在不对称现象，它是由许多的个体所组成。一般来说，网络密度，出度、入度中心势，中介中心势等是衡量隐性知识网络不对称的重要指标，这些指标对隐性知识传播网络的反映也各有不同。文章通过平均场理论分析了隐性知识传播行为，构建起隐性知识网络传播模型，并对该模型进行了计算机数值仿真。

隐性知识；网络传播；行为分析

1 隐性知识的传播

隐性知识是一种在长期的实践中通过不断地积累总结而产生的、不易通过言辞表达、不易传播与共享的带有个性色彩浓厚的实践经验性知识，它是植根于人们在工作生活中的一些观察、经验与顿悟所得，往往以经验、技巧、感觉、观察能力、特长、思维模式、价值观、组织文化等形式表现出来。

在隐性知识传播过程的研究中，不同的学者进行了不同的研究，日本学者 Nonaka和Takeuhci(1995)提出的知识螺旋模式最为著名[7，8,9],阐述了知识转换的过程为社会化→外化→结合→内化→社会化→外化→ …，在显性知识与隐性知识持续的循环转换中不断进行新的知识创造。Hedlund(1994)提出了通过显性与隐性知识在个体、集体、组织和组织间相互传播的一个知识交换模型。Eriksson和Dickson(2000)阐述了由IT基础设施、推动者、知识传播流程以及组织价值观、规范与程序这四个影响因子构成的一个知识传播与创造的模型。单雪韩(2003)提出，知识传播者的知识外化与知识接受者的知识内化构成了整个知识的传播过程。谭大鹏与霍国庆 (2006)在总结前人的研究后，提出了三个知识传播过程阶段，也就是准备、传递与整合三个阶段，并且他们还创建了一般知识传播模式[11，12]。

从信息传播角度，Hendriks(1999)指出知识的特性决定了其不可以像商品那样自由传播，知识接受者在接受知识的时候也要知道如何重建知识，知识接受者必须有能力在学习的同时还要能传播知识。Jim Botkin(2000)提出知识传播的发送方与接受方必须要有联系才能实现知识的传播；所以说知识传播就是两个事物之间的联系与传播，这两个事物可以是个体与个体，可以是个体与组织，也可以是组织之间。Connelly和Kelloway(2003)认为信息在两者间交换或者是帮助对方的行为的汇集就是知识传播[7，8,11]。

2 隐性知识网络传播过程

隐性知识传播网络是由若干个个体组成的网络，如果个体A向B传播知识，但B个体不一定向A传播知识，这样，可以说这种传播网络是非对称的[10]。网络传播节点由诸多个体组成，它们相互间的联结就构成了多种网络联系，各种知识就可以通过这些联系进行传播。一般来说，出度、入度中心势，网络密度，中介中心势等是衡量隐性知识网络不对称的重要指标，而这些指标对隐性知识传播网络的反映也各有不同：

（1）网络密度是衡量网络节点间紧密程度的重要指标，L/[N（N-1）]是其计算公式，N和L分别代表网络节点数以及网络中弧的条数。在知识网络传播中，如果一个组织的人际网络密度太高，将会降低组织的网络传播的效率，从而浪费较多的精力，进而超出预期维护的成本；反过来，如果一个组织的人际网络密度太低，则表示人们之间的关系不密切，这样也不利于提高知识传播与共享的效率。

（2）就网络节点的出入度中心势问题而言。鉴于网络存在知识的不对称性，这必然导致每个节点在网络中传播截然不同，是否能精确计算每个节点的出入度中心势是解决问题成败的关键。多个节点的联结进而生成了组织隐性知识传播的网络，隐性知识传播效率的高低与节点的行为特性息息相关。我们可以通过节点的出入度中心势反映每个节点与其他节点之间的直接联系。节点出度可以表示为其代表节点vi对其他节点传播影响的程度。其值俞大，说明vi节点向其他节点传播的知识愈多，该节点地位愈高，所起的作用也愈大；节点入度可表示为：其代表节点vj吸收其他节点知识个体数量的多少，同样可以得出其值愈大，吸收其他节点知识的能力愈强的结论。

基于上述的分析，在整个隐性知识传播网络中，其出入度中心势的计算公式如下：

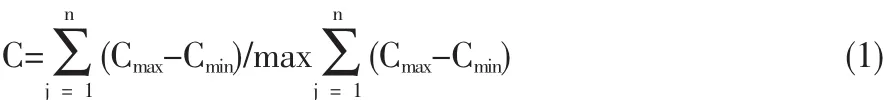
其中V(i)理解为第i个节点的出入度值，Cmax为所有节点出入度的峰值。

（3）当网络中的某个节点置身与其他的节点之间时，为了更好地反映网络中个人成员在整个不对称隐性知识网络传播过程中自身的状况，一个新的概率—中介中心势必须作解释，其公式如下：

其中，经过i-j节点的所有路径总量用gik表示；在gij中，其经过k节点的路径的总量用gikj表示。

3 隐性知识网络传播模型

本文借鉴研究文献[1,2,3,4,5]对传染病的研究成果，构建了隐性知识网络传播的传染性模型，通过计算机模拟仿真证明了该模型。我们假定隐性知识网络传播的网络在一定时点上的节点数不变，并且假定可以把网络节点分为隐性知识易感S，隐性知识潜伏E，隐性知识传播I，和隐性知识隔离Q四种状态，定义时刻时各状态节点所占的比例为S(t)，E(t),I(t),Q(t)并进一步约定ρ1,ρ2分别表示隐性知识潜伏类和隐性知识传播的传染率，ε表示隐性知识潜伏类成为隐性知识传播的比例；γ为隐性知识隔离率，δ为隐性知识恢复率，即由隐性知识隔离类又成为隐性知识易感类的比率。 其中 ρ1,ρ2,ε,γ,δ 均为正常数[11,12]。

对于均匀网络，度高度峰化，度扰动很小，近似为平均度，即 ki≈，如图 1所示，根据平均场理论[11,12]，得出隐性知识SEIQ模型的传播动力学方程如所示:

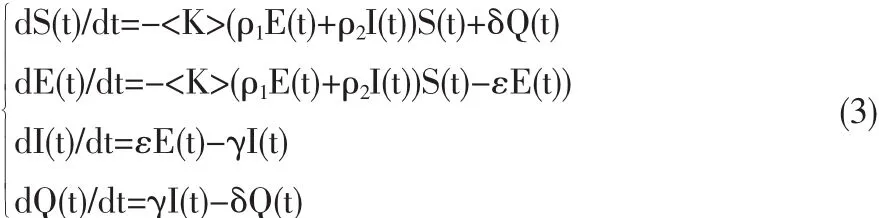
利用归一化条件S(t)+E(t)+I(t)+Q(t)=1，代入(3)，消去S(t)，则系统可归结为下列三维模型：

可以得出，D是系统(4)的正向不变集，隐性知识网络传播系统(4)的零点是其平衡点，故系统(3)有平衡点(1,0,0,0)，该平衡点可以为系统(3)的隐性知识网络传播平衡点。

现在我们寻求系统(3)在D内的其他平衡点，令系统(4)的右端等于零，用I表示所有其它变量，则有：

其中 ρ=(ρ1E(t)+ρ2I(t))，所以 I(t)+γ/ρI(t)+γ/εI(t)+γ/δI(t)=1

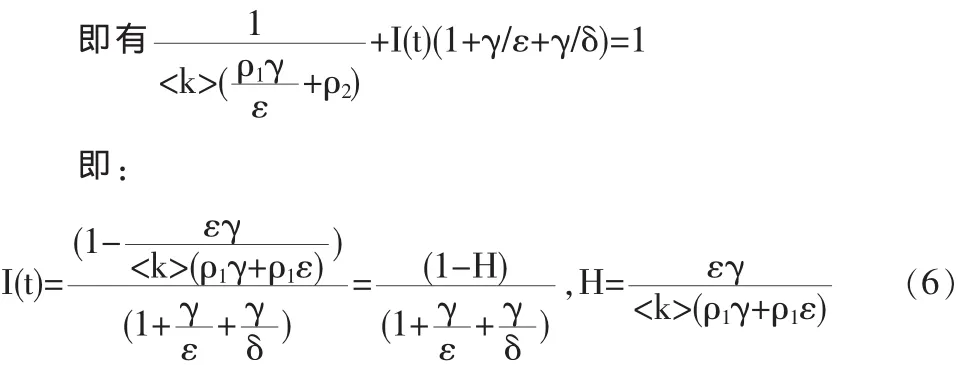
可见，当H<1时，系统（3）在内存在唯一的正平衡点(S*,E*,I*,Q*)，其中 S*,E*,I*,Q* 分别由（5）（6）两式给出，当 H≥1时，系统（3）只有唯一平衡点(1,0,0,0)，不存在正平衡点，这里H=1的即为我们关心的隐性知识网络传播阈值。

4 隐性知识网络传播系统平衡点的稳定性讨论

由于系统（3）的隐性知识网络无效传播平衡点，与系统（4）的零平衡点想对应，因此，只需将系统（4）的零平衡点的稳定性考虑在内即可[11,12]，我们有如下引理：

引理 1：平衡点(S,E,I,Q)=(1,0,0,0)是系统(1)的局部稳定解，记，当 H≥1 时，系统（3）收敛于(1,0,0,0)，称其为隐性知识网络无效传播平衡点。

将系统（4）的右端在原点线性展开，容易得到其特征方程的三个特征根均具有负实部，故由Routh-Hurwits判断[6]，即知零平衡点是局部渐进稳定的，即当H≥1时，系统(1)收敛于(1,0,0,0)，即隐性知识网络无效传播平衡点。

引理2:平衡点(S,E,I,Q)=(S*,E*,I*,Q*)是系统(1)的局部稳定解，当H<1时，系统(1)收敛于该平衡点，称为隐性知识网络有效传播平衡点。

证明:对于 H<1时，系统(1)的平衡点为(S*,E*,I*,Q*)，在

该矩阵的特征值由下列的3次特征方程[11,12]

由Routh-Hurwits判断[6]，则方程（7）的所有特征根均具有负实部，这就证明了隐性知识网络有效传播平衡点是局部渐进稳定的，即当H<1时，系统(1)收敛于(S*,E*,I*,Q*)。

5 隐性知识网络传播传染曲线仿真

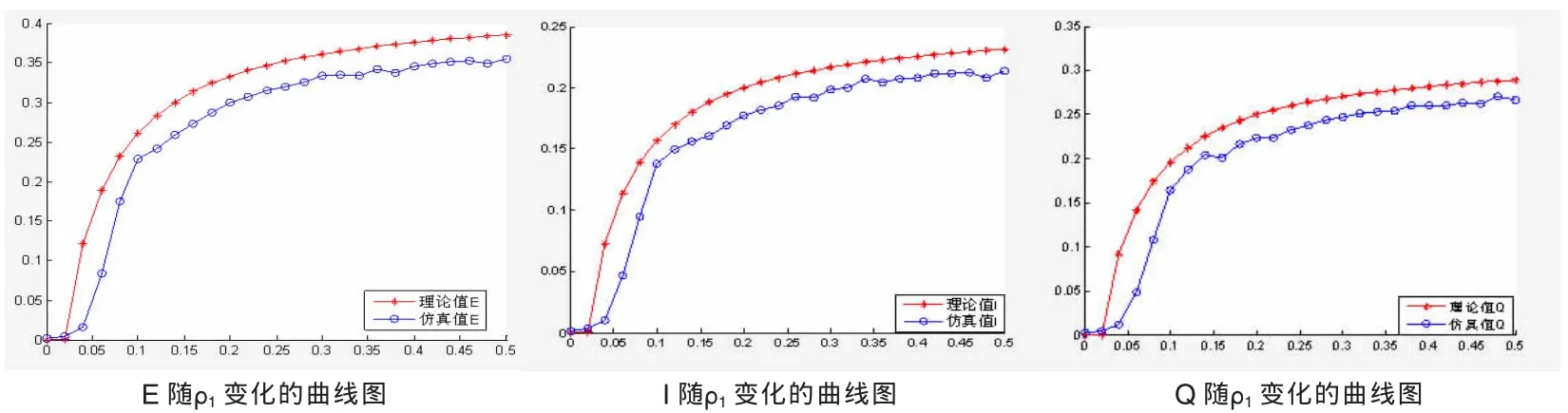
我们取参数N=5000,m=4,p=0.5的小世界网来验证平均场近似的合理性，另外，取定参数ε=0.3,r=0.5,δ=0.4，取20个网络现实，每个现实做40次传播，然后取平均，当ρ2=0.05时，E,I,Q分别随ρ2变化的曲线的模拟结果见图2，当ρ1=0.02时，E,I,Q分别随ρ2变化的曲线的模拟结果见图4，由图可知，当ρ2=0.05，ρ1=0.03时，阈值H=1，与理论值符合得较好。

所以，本文借鉴SEIQ类传染模型[11,12]，对隐性知识网络传播行为进行了仿真过程的演示，基于平均场理论和数值的基础，对均匀网络上的传播临界的特性进行了模拟研究。研究结果表明：对于隐性知识均匀网络，存在隐性知识传播临界阈值且该阈值与隐性知识隔离率、隐性知识潜伏期的隐性知识传播等有关，隐性知识传播行为具有网络性。

[1]Newman M E J.Spread of Epidemic Disease on Networks[J].Physical Review E，2002，66(1).

[2]许丹，汪小帆.局域世界复杂网络中的病毒传播及其免疫控制[J].控制与决策，2006，21(7).

[3]Xia C Y，Liu Z X，Chen Z Q，et al.Dynamic Spreading Behavior of Homogeneous and Heterogeneous Networks[J].Progress in Natural Science，2007，17(3).

[4]李光正，史定华.复杂网络上SIRS类疾病传播行为分析[J].自然科学进展，2006，（3）.

[5]夏承遗，刘忠信，陈增强，袁著祉.复杂网络上带有直接免疫的SIRS 类传染模型研究[J].控制与决策，2008，23（4）.

[6]陈兰荪，陈键.非线性生物动力系统[M].北京:科学出版社，1993.

[7]丛海涛，唐元虎.隐性知识转移、共享的激励机制研究[J].科研管理，2007，(1).

[8]刘志国,崔健.医院科技创新与隐性知识共享[J].中国医院管理,2006，(5).

[9]张方华.知识型企业的社会资本与知识获取关系研究[J].科学学研究,2006,24(1).

[10]王夏洁,刘红丽.基于社会网络理论的知识链分析[J].情报杂志,2007,(2).

[11]林向义.知识不对称网络中隐性知识共享的分析与优化[J].情报科学，2008,（2）.

[12]楚扬杰;周佳华.SEIQ类疾病在小世界网络上的传播行为分析[J].计算机工程与应用，2009，（3）.

(责任编辑/亦 民)

R197.3

A

1002－6487（2011）03－0082-03

曹 征（1978-），男，湖南郴州人，博士研究生，中级经济师，研究方向：知识共享研究。