基于多层线性模型的就业影响因素研究

游达明，杨晓辉，杨 立，丁 燕

（中南大学 商学院，长沙 410083）

基于多层线性模型的就业影响因素研究

游达明，杨晓辉，杨 立，丁 燕

（中南大学 商学院，长沙 410083）

当前就业问题已成为困扰各国政府的世界性难题，对于我国这样一个人口大国尤为突出。文章针对我国就业问题，建立了影响我国就业情况的分层模式指标体系，且通过以就业人数为因变量，各影响因素为自变量的逐步回归模型消除影响因素间多重共线性，得到了影响就业的主要因素。在此基础上，以样本单位为第一水平，样本所在地区为第二水平，建立了关于就业的分地区二层线性模型。

多层线性模型；就业；因果检验；宏观经济

0 引言

就业问题是困扰各国政府的世界性难题。我国是一个人口大国，在当前现代化、工业化、城市化建设进一步加快的历史进程中，劳动力供求总量矛盾与结构矛盾并存，城镇就业压力加大与农村富余劳动力转移速度加快同时出现，新增劳动力就业与失业人员再就业问题相互交织，既要承继人口增长的惯性压力和体制转轨的失业压力，又要面对工业化升级中就业弹性系数不断降低的趋势，迫切需要用正确的理论来解答中国就业问题并为其提供指导，提出相应的政策。

当前，就业问题已经成为经济发展中最重要的问题之一，国内外对此进行了广泛的研究。在亚当·斯密和大卫·李嘉图的早期经济理论中就对就业问题进行了分析，凯恩斯的新古典经济学派又对这一问题进行了研究。西方对就业问题的代表模型有贝弗里奇的结构性失业模型和菲利普·阿吉翁等提出的就业失业模型。总体上而言西方经济学观点认为经济增长是就业增长必然会带来就业增长[1]，这也是奥肯定律的内容。但是，近年研究表明，这些理论与我国现实有一定的矛盾[2]，国内学者又提出了一些新的理论。

李敏[3]在分析中国就业症结时认为有以下原因：

①由累积因果过程与二元结构所引发的内在需求冲动。②效率工资的居高不下削弱了中国劳动力成本低的优势。③缺乏大量的熟练技术工人的技术性约束。④跨国公司本身的技术刚性的限制。⑤政府政策不当造成的资源配置发生扭曲。⑥忽视经济与人协调发展引发就业问题的理论分析。还有其他的对就业问题与居民收入关系的研究[4]，与经济增长关系的研究[5]，与技术进步关系研究[6]等。

虽然多位学者对我国的就业问题进行了多角度的研究，但是当前的研究还存在以下两方面局限：

第一，侧重从某一角度或某一因素研究就业问题，没有从宏观上整体上研究影响就业水平的各个因素，忽略了因素之间的联系。

第二，在研究多个影响就业水平的因素时，没有考虑因素的层次性，单纯将其全部划分到一个层次研究，这样会导致结论不准确，甚至是错误的。

本文正是着眼于上述两方面局限，对就业问题进行进一步的研究。首先，采用Granger因果检验方法，对已有的理论提出的就业水平影响因素进行验证，筛选出影响就业水平的主要因素，通过逐步回归的方法消除共线性，最终确定出影响就业水平的因素或指标。在此基础上，采用多层线性模型，克服各因素之间的层次影响。多层线性模型（简称HLM)，由Lindley和Smith在1972年提出，并于上世纪90年代形成了完善的体系[7]。该理论问世，解决了一个困扰统计学半个世纪的问题，既不同层次的数据处理问题。本文正是基于该理论，充分考虑各个因素之间的层次关系，确定出就业水平模型。

1 就业水平影响因素的指标体系建立

由问题分析中，可以初步了解到当前就业是我国社会和国民经济中极其重要问题，根据我国目前现状和已有的相关文献资料知道，影响就业的因素可能有很多。而该问题要求对有关统计数据分析，寻找影响就业的主要因素或指标。如何在庞大的宏观经济体系中寻找影响就业的主要因素是该小节研究的重点。

1.1 就业问题评价指标（因变量Y）选取

就业是社会、国民经济中极其重要问题。按已有研究，就业可以定义为三个月内有稳定的收入或与用人单位有劳动聘用关系。本文是对就业人数进行研究，所以选取就业人数作为就业问题评价指标。

1.2 影响因素指标体系建立

影响就业的因素可能有很多，这些因素之间内部可能也存在相互之间的关系，如何系统明了地对这些因素进行分析，找到主要的影响因素的首要条件是建立合理的指标体系。

1.2.1 指标体系建立方法选取

通过参考各关于指标体系的文献，本文采用分层模式指标体系，将整个指标体系分为三层，第一层为目标层，第二层要素层，第三层为指标层；根据对各类指标的定性分析，可以认为该问题采用分层模式指标体系的目标层为“影响因素”。接下来讨论研究要素层各要素的选取和定义。

1.2.2 要素选取

参考我国宏观经济指标体系，和讯网数据库和囯研网数据库，以及从宏观角度看，消费、投资、政府购买和进出口都是影响就业的重要因素，再综合文献中的资料，本文选取就业影响的指标体系要素层的三个要素分别为：（1）消费；（2）投资；（3）对外贸易；

1.3 各要素主要指标初步选取

1.3.1 消费要素

根据宏观经济核算指标，了解到反映其消费要素的指标可能有：居民消费价格指数、衣着价格指数、粮食价格指数、居住价格指数、交通和通信价格指数，社会各种消费品零售总额和居民收入等。由于衣、食、住、行价格指数综合起来就是居民消费指数，所以这几个指标就可以选择居民消费价格指数；社会消费品零售总额可以代表社会整体消费品水平，可以反映居民消费；而反映居民消费水平的要素可以包括居民实际收入和可支配收入，所以可以用其中一个指标表示，这里采用居民可支配收入这个指标。

1.3.2 投资要素

整体反映投资要素的指标是固定资产投资完成额，而固定资产投资包括中央和地方投资两项，所以再选取另一个指标——地方项目资产投资完成额。

中央投入中教育科技等投资，间接影响了人力资本的强度，从而影响到就业，这一系列的影响过程涉及很广，在接下来的模型中可以暂不考虑其影响。

市场利率是影响就业的一个很重要的指标，它可以直接影响投资情况，所以考虑将“市场利率”这个指标放入“投资”这个要素中。

1.3.3 对外贸易要素

对外贸易中的主要指标有进出口额，进出口总额，进出口差，其中进出口差最能反映对外贸易这个要素的情况，所以考虑只选取“进出口差”和“进出口总额”这个指标。

综合以上分析，得到影响因素指标体系见表1。

表1 影响就业因素指标体系

指标注释如下：

（1）固定资产投资完成额：选取本期累计数比上年同期增长比例；地方项目资产投资完成额：选取本期累计数比上年同期增长比例；场利率：为同业拆借加权后的指标值。

（2）居民消费价格指数：选取本期数，以上年同期为100；社会消费品零售总额：选取本期累计数与上年同期增长比例；城镇居民可支配收入：选取本期数。

（3）进出口差：选取进出口差的本期数；进出口总额：选取进出口总额的本期累计数与上年同期增长比例。

1.4 样本选取

综合各数据库各指标的数据，由于年度数据样本量太小（一般从1978至2008，且1989年前缺失值严重），本文选取月度数据（2001年1月至2009年7年）作为数学模型建立的所需的统计数据。数据来源于囯研网。

各影响因素指标可以查询到月度数据，而根据就业的定义和数据库中数据，只能得到就业人数的年度数据。本文中利用三次样条插值法，利用2001年至2008年的年度就业人数进行数据处理，得到2001年1月至2009年7月的月度数据。经过各数据整理，得到就业指标数据如表2。

1.5 因果关系检验提取主要指标

通过以上定性的分析，我们选取了8个可能的主要因素指标，并选取了2001年1月至2009年7月的样本数据，现将对这些样本数据进行Granger因果关系检验，通过检验找到这8个指标中对就业人数影响的主要因素。

1.5.1 Granger 因果关系检验原理

两个时间序列的变量在时间上有先导——滞后关系，如何考察一个变量过去的行为是否在影响另一个变量的当前行为，或者双方的过去行为在相互影响着对方的当前行为，Granger提出了一个简单的检验程序，称之为Granger因果关系检验。

对两个变量Y与X，Granger因果关系检验要求估计以下回归：

表2 就业指标表

表3 就业人数与固定资产投资完成额Granger因果检验结果表

表4 就业人数与各因素的Granger因果检验结果

可能存在四种检验结果：

①X对Y有单向影响，表现为（1）式X各滞后项前的参数整体不为零，而（2）式Y各滞后项前的参数整体为零；

②Y对X有单向影响，表现为（2）式Y各滞后项前的参数整体不为零，而（1）式X各滞后项前的 参数整体为零；

③Y与X间存在双向影响，表现为Y与X各滞后项前的参数整体不为零；

④Y与X间不存在影响，表现为Y与X各滞后项前的参数整体为零；Granger检验是通过受约束的F检验完成的。如针对X不是Y的Granger原因这一假设，即针对（1）式中X滞后项前的参数整体为零的假设，分别做包含与不包含X滞后项的回归，记前者的残差平方和为RSSu，后者的残差平方和为RSSR；再计算F统计量：

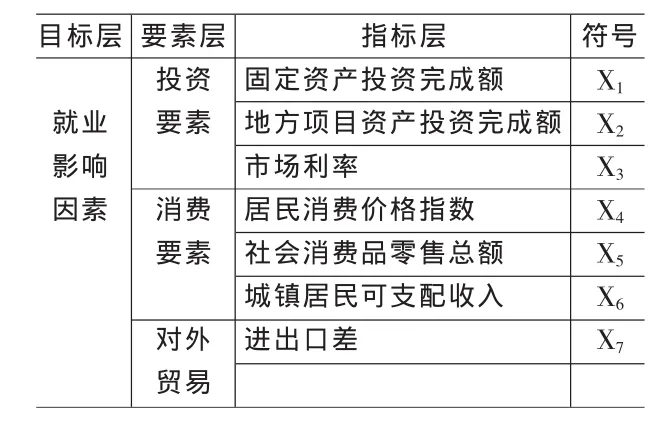
表5 影响就业人数的主要指标

表6 随机效应模型输出表

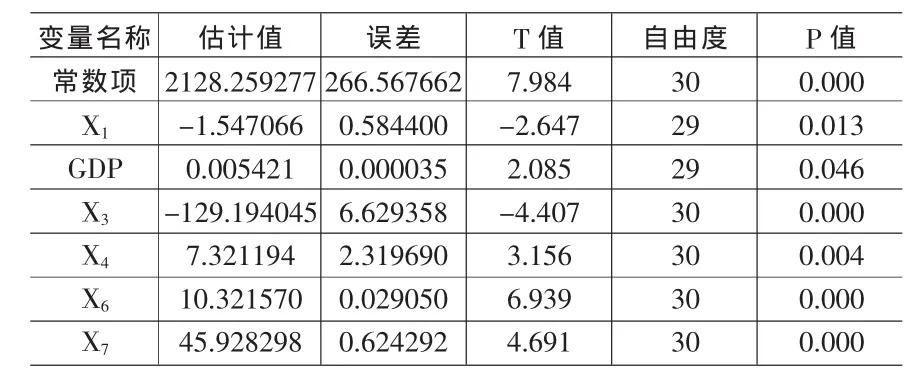
表7 完整二层线性模型系数表

式中，m为X的滞后项的个数，n为样本容量，k为包含可能存在的常数项及其他变量在内的无约束回归模型的待估参考的个数。

如果计算的F值大于给定显著性水平α下F分布的相应的临界值Fα(m,n-k)，则拒绝原假设，认为X是Y的Granger原因。

1.5.2 Granger因果检验

表2中给出了就业人数和8个指标的样本数据，对这些样本数据进行因果关系检验。用Eviews先对就业人数和固定资产投资完成额进行因果关系检验，得到如表3的结果。

由表3F检验的相伴概率可以看出，在5%的显著性水平下，拒绝“X1不是Y的Granger原因”的假设，而不拒绝“Y不是X1的Granger原因”的假设。因此，检验结果为：固定资产投资额是就业人数的Granger原因。

同理，将就业人数与其他因素指标进行Granger因果检验，得到如表4的结果。

综上可得以下结论：

(1)固定资产投资总额、地方项目资产投资、市场利率、居民消费价格指数和社会消费品零售总额是就业人数的Granger原因，但是就业人数不是它们的Granger原因；

(2)城镇居民可支配收入和进出口差额是就业人数的Granger原因，同时就业人数也是它们的Granger原因；

(3)进出口总额不是就业人数的Granger原因，就业人数也不是进出口总额的原因；

1.5.3 主要指标确定

以上表中的因果关系检验结论为依据，是就业人数的Granger原因的指标为影响就业人数的主要指标。则表示为如表5所示。

由上述分析可知，影响就业人数的相关因素由表5所示的七个，为了消除因素之间的多种共线性，以就业人数为因变量，表5中的影响因素为自变量，以2001年1月至2009年7月的全国月度数据为样本，建立逐步回归模型，得到以下回归结果：

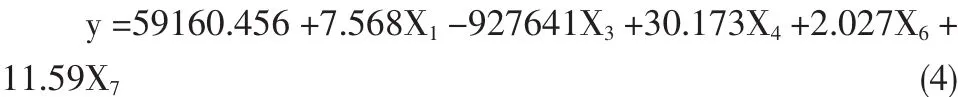
由此可见影响就业问题的主要因素为 X1，X3，X4，X6，X7，在后续的多层线性模型，我们仅考虑这五个因素的影响。

2 多层线性模型建立

多层线性模型（HLM）是分析具有层次结构数据的一种新型统计分析技术，与传统统计方法相比，具有模型假设与实际更吻合、结果解释更合理等特点。近年来这一方法的应用逐渐在社会科学的研究中受到重视。具体而言，多层线性模型(HLM)有5个方面的优点[8]：(1)考虑了不同层次的随机误差和变量信息,其标准误估计、区间估计和假设检验更加准确和有效;(2)可以通过计算不同水平变异在总变异中所占的比率来确定不同水平对因变量的影响程度；(3)可以作为结构方程模型的拓展,用来分析具有多层结构的潜变量之间的因果关系,建立多水平结构方程模型;(4)可以分析重复测量的数据,即将测量看作第一水平,将测试个体看作第二水平;(5)可以分析离散型的数据资料,如二项分布和泊松分布的数据等。

本文从各地区差异性考虑，建立多层线性模型。该问题可以看成一个两水平模型。第一个水平为样本单位；第二个水平为样本所在地区。第一水平方程与线性回归方程相似，但其截据和斜率为随机变量；第一水平方程的截据和斜率依赖于第二水平的自变量，从而构成两水平模型。在该问题中，因变量为数值形式，可以建立以因变量为数值变量的两水平模型。

2.1 随机效应回归模型

由逐步回归模型可知，影响就业的主要因素为X1，X3，X4，X6，X7。 所以选取了 X1（固定资产投资）,X3（市场利率）,X4（居民消费价格指数）,X6（城镇居民收入）,X7（进出口差）五个指标作为自变量，用Y（就业人数）作为因变量建立随机效应二层线性回归模型，并采用统计软件HLM 6.0.2求解。

步骤一：第一层

根据该模型中第一水平：

的原理进行参数估计。因变量为Y，自变量为X1，X3，X4，X6，X7

步骤二：对第二层进行参数估计。

第二水平：

则有HLM 6.0.2的输出结果见表6。

得到随机效应回归模型如下：

由式（7）可以看出当加入地区的因素后，Y 随 X4，X6，X7的增加而增加，随X3的增加而减少，随X1的增加而减少。X3是市场利率，显然该结论符合实际情况。然而当X1（投资）增加，Y（就业人数）减少，该结论不同于逐步回归模型（4）中X1（投资）增加，Y（就业人数）增加的结论，这种差异性可能归因于地区层次作用的控制作用。进一步考虑完整的二层线性模型。

2.2 完整二层线性模型

由（7）分析得出地区层次的控制作用对X1的影响是最大的，由原来的正相关关系转变为负相关关系，所以考虑对在第二水平上加入影响地区的自变量。在宏观经济中，GDP能较全面反映经济发展状况，而关于就业而言，地区的差异性主要体现在经济的差异性上，所以，在第二水平对β1j加入新的自变量——地方GDP。所以模型为：

第一水平：

第二水平：

则HLM6.0.2的输出结果见表7。

得到完整二层线性模型如下：

比较（7）和（15），得知当在 X1的第二层加入 GDP这个自变量后进行回归，X3、X6、X4和 X7前的系数几乎没什么变化；且X1的系数加入GDP这个自变量后，GDP每增加一个单位，固定投资完成额对就业人数的影响 (斜率)就减少0.00542个单位，表明第二层的某变量每变化一个单位，在其他变量恒定的情况下，第一层上相应的回归斜率或截距就变化“该第二层变量的系数值”个单位。这很好地解决了（7）中X1系数为负的问题。如此证明了该模型的合理性；又当任一地区指标值代入（7）中，均能得到该地区对应的Y（就业人数）值。从表7可以看出，本模型各个拟合参数都比较理想，是一个较好的理论模型。

3 结论及研究展望

本文首先对影响就业水平的因素进行了筛选和验证，得到了五个主要的影响因素。在此基础上，通过引入GDP的间接效应，建立了就业水平二层线性模型，从拟合参数来看，模型效果较为理想。

考虑到就业这一宏观经济问题，受到了多层次的因素影响，本文采用了多层线性模型对其进行了探索性研究，后续研究可以进一步深化。在本文中，以分地区为例，建立多层线性模型。该模型适用于多水平回归问题，同样可以将该模型应用到其他方面，如考虑到行业，就业人群等因素。建立三水平模型，甚至是四水平问题。此外，对具体的影响因素，可进行进一步研究，建立更加精确的模型，为我国宏观经济政策提供参考。

[1]Martine Carre,David Drouot.Pace Versus Type the Effect of Economic Growth on Unemployment and Wage Pattern[J].Review of Economics Dynamics,2004,(7).

[2]李晗等.奥肯定律在中国的适用性分析[J].商业研究，2009，386.

[3]李敏.中国就业问题研究[D].华中科技大学,.

[4]王春超.中国农户收入增长与就业决策行为:一个动态解释[J].统计研究，2008，28（5）.

[5]胡鞍钢等.经济增长转型与就业促进[J].数理统计与管理,2004，24（6）.

[6]Moglu.D.Technical Change，Inequality and the Labour Market[J].oumal of Eeonomic Literature,2002，(40).

[7]张雷,雷雳,郭伯良.多层线形模型应用[M].北京:教育科学出版社,2003.

[8]蔡永红等.统计在社会科学领域应用的新进展及反思[J].统计研究，2006，（2）.

(责任编辑/浩 天)

O212

A

1002－6487（2011）03－0041-04

国家社会科学基金重大资助项目（07&ZD023）；教育部新世纪优秀人才支持计划资助项目（NCET-08-0578）；教育部哲学社会科学研究重大资助项目（08JZD0016）

游达明（1963-），男，湖南益阳人，教授，博士生导师，研究方向：技术经济。