一种局部线性嵌入的空间听觉重建方法

汤永清, 方 勇, 黄青华

(1.上海大学通信与信息工程学院,上海 200072;2.丽水学院计算机与信息工程学院,浙江丽水 323000)

一种局部线性嵌入的空间听觉重建方法

汤永清1,2, 方 勇1, 黄青华1

(1.上海大学通信与信息工程学院,上海 200072;2.丽水学院计算机与信息工程学院,浙江丽水 323000)

空间听觉重建中,头相关传输函数 (head-related transfer function,HRTF)庞大的数据量是影响虚拟声源合成效率的主要因素之一.为了减少 HRTF的数据存储,提出一种局部线性嵌入 (locally linear embedding,LLE)空间听觉重建方法.通过LLE对高维 HRTF数据进行降维,在低维数据空间提取与方位感知相关的特征,然后利用聚类算法进行分类,得到特征 HRTF,而其余非特征 HRTF则可以利用特征 HRTF通过改进插值算法进行重构.与现有的主成分分析法 (principal component analysis,PCA)相比,利用LLE降维后的数据保留了更多的感知信息,利用 HRTF数据间的内在关系,对插值后的数据进行修正,可减少重建误差.仿真结果表明,该方法能够有效地减少 HRTF的存储数据量,有利于提高虚拟声源的合成效率.

头相关传输函数;局部线性嵌入;流形;空间听觉重建

空间听觉研究的目标是建立与声源方位相关的听觉环境.已有研究表明,人耳对声源位置的判断取决于声音到达双耳时的耳间时间差、耳间能量差、频谱形状、听觉经验以及环境等因素[1-3].声波经过媒质传输到达双耳时,会受到人的躯干、肩膀、头部,尤其是耳廓的衍射和滤波,整个过程相当于一个声学滤波器.通常将该滤波器建模成头相关传输函数(head-related transfer function,HRTF)或头相关冲激响应(head-related impulse response,HRIR).HRTF或 HRIR包含着关于声源方位的全部特征信息,在空间听觉或虚拟现实中起着非常重要的作用,比如可以通过 HRTF合成任意方位的虚拟声源等.Huang等[4-5]研究了在球谐波域中的插值方法,以及个性化HRTF.在利用 HRTF进行虚拟声源的合成过程中,为了产生逼真的听觉效果,研究者们提出了很多HRTF模型[1,6-7],但大都需要较大的 HRTF数据存储量或较复杂的计算量,从而在应用上影响了虚拟声源的合成效率.

在模式识别和人工智能领域,为了提高算法或系统的“智能水平”,需要借助对人类认知的过程、心理以及生理的研究成果[3,8],即大脑对外界事物的认知是建立在对其部分感知的基础之上.因此,本研究提出一种基于非线性流形学习算法——局部线性嵌入 (locally linear embedding,LLE)的空间听觉重建方法.

1 HRTF数据特征

HRTF是当声源位于头部周围不同方位时所测得的频率响应,是多种因素共同作用所产生的序列.影响 HRTF的因素很多,而声源的方位 (包括水平方位角θ、垂直方位角 φ)是其中最重要的因素之一.

就人的听觉而言,不同方位角的 HRTF既有相似之处,也有各自不同的方位特征.方位角差异越小,其对应的 HRTF数据间的“距离”越小,共性越多.为了定量地描述声源所处的不同垂直方位角与其所对应的 HRTF之间的关系,下面分别从 HRTF数据的距离以及相关系数两方面加以说明.

(1)HRTF数据的距离.

角度坐标如图 1所示.欧氏距离定义为

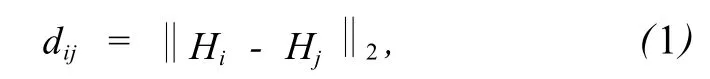
式中,H表示 HRTF数据,i,j对应不同的方位角.图2为声源在垂直面内取不同方位角 φ时 (θ=0°),HRTF之间的欧氏距离灰度图,其中横、纵坐标均表

图 1 角度坐标Fig.1 Angle coord inate

图 2 各垂直方位角对应的 HRTF之间的距离(θ=0°)Fig.2 D istance between HRTF correspond ing angles respectively(θ=0°)

示垂直方位角.

(2)HRTF数据的相关系数.相关系数的定义为

式中,N为 HRTF的序列长度,⊙表示 Hadamard积,,分别表示第 i个和第 j个 HRTF的方差.图 3为θ=0°时,各垂直方位角对应的 HRTF之间的相关系数.

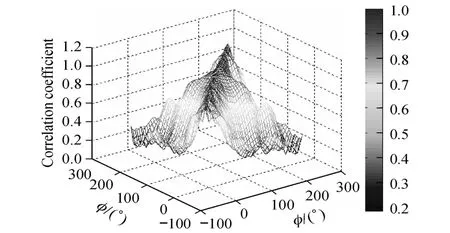
图 3 各垂直方位角对应的 HRTF之间的相关系数(θ=0°)Fig.3 Correlation coeff icients of HRTF between elevation s(θ=0°)

从图 2可以看出,某一垂直角对应的 HRTF和其邻近垂直角对应的 HRTF有较小距离,当角度差异增大时,HRTF之间的距离也随之增大,即相隔较远的垂直角度对应的 HRTF之间的数据关联性减弱.图 3中的 HRTF之间的相关系数说明,邻近方位的 HRTF之间具有较强的相关性,而当垂直角度的差异变大时,这种相关性就会减弱.因此,在对HRTF进行重构时,可以只保留邻近角度的几何性质,利用局部邻近角度的 HRTF进行线性加权重构,这样只需求解一个小的线性方程组,所需要的计算量较小.

2 降维算法及 HRTF特征提取

在聚类之前,通常对高维数据先进行降维处理,已有研究均是利用主成分分析 (p rincipal component analysis,PCA)对 HRTF进行降维[2,9].通过对 HRTF数据所构成的自相关矩阵进行特征值分解,选取特征值相对较大的特征向量所组成的空间作为信号空间,忽略特征值相对较小的特征向量所组成的噪声空间,从而达到数据降维的目的.PCA算法本质上是通过特征向量的线性组合进行降维,属于线性降维方法.但是,当数据不满足 PCA的模型假设时,即当数据不能由特征向量的线性组合表示时,则需要寻找一种新的降维方法.

在人脸识别的研究[10]中发现,流形 (manifold)在人脑认识事物的过程中起着至关重要的作用.流形是局部具有欧氏空间性质的空间,由多个局部呈线性关系的小曲面连续联接而成.人脑认识事物总是先通过对事物的若干关键因素的理解,继而形成对事物的整体认识.人脑从由低维数据所形成的多个不同流形中综合认识由高维数据所组成的事物,如人脸.因此,根据对人类感知机理的分析,当事物的数据特征不能简单地描述成特征向量的线性组合,而数据的局部表现出较强的关联性时,适合采用非线性流形学习算法.

非线性流形学习算法已广泛应用于人脸识别,将该方法引入到空间听觉中来,是基于以下原因:①人脸数据与听觉数据均是与人类感知有关的数据,与传统的线性降维方法相比,该类方法使得降维后的低维空间数据能够保留更多的感知信息,发现数据间的内在关系;②从 HRTF数据特性来看,HRTF间的相关性随着声源方位角差异的变大而减弱,某一方位的 HRTF只与邻近方位的 HRTF具有较强的相关性,因此,可以通过少数邻近方位角的 HRTF对该方位 HRTF进行线性加权重构.

LLE[8]作为一种非线性流形学习算法,其基本思想是在数据点与其邻域点之间构造一个重构权向量,并在低维数据中保持权值不变,即假设嵌入映射在局部为线性的条件下,最小化重构误差.LLE算法中关于数据局部线性的假设与 HRTF的数据特性一致,因此,LLE可以作为 HRTE数据的降维工具.

假设存在高维数据 X为一个 D×N的矩阵,即

X=[X1,X2,…,XN]. (3)

给定数据集:X={Xi∈RD|i=1,2,…,N},可以找到映射函数 f,使{Yi=f(Xi)|i=1,2,…,N}满足,其中Y={Yi∈Rd|i=1,2,…,N},d≪ D,Y为降维后的数据集.

LLE算法可以进行如下描述.

(1)求向量 Xi的 K个最邻近向量以及相应的权值,由于局部邻域内的数据表现出线性关系,因此,Xi可以用 K个最邻近向量的线性加权和进行估计.

真实值与估计值之间的误差可用代价函数ε(W)表示为

式中,Wij表示第 j个数据对第 i个估计向量的贡献,Xj为 Xi的 K个最邻近向量集中的一个.为了计算Wij,可将代价函数ε(W)最小化,并且要求 Wij满足两个约束:①若 Xj属于 Xi的邻近向量集,则②若 Xj不属于 Xi的邻近向量集,则Wij=0.从而得到两个新的矩阵W和H,分别存储权值以及最邻近向量的索引.

(2)将高维向量 Xi映射到低维空间中,得到数据 Yi,而向量之间的权值和邻近关系保持不变.降维后的数据 Y中包含着高维数据的特征,同时使得维数远小于原有数据的维数,有利于进行分类处理.

3 分类算法及插值算法

3.1 分类算法

HRTF数据之间既有区别,又互相联系,在分类前并没有一个非常明确的类别区分标志,因此,适宜采用无监督的学习分类算法——k-均值分类算法.该算法的目的是将降维后的数据划分成 k类,使得各个向量到其对应的聚类中心向量的欧氏距离最短,即类内平方和最小.根据平方误差准则,代价函数可以写为

式中,Yi为被分类的数据集,表示 Y的均值,Nclass为经验值,表示需要分类的数目,可以通过多次实验的方法获得.uij有两个约束:①当 Yi不属于第 j类时,uij=0;②当 Yi属于第 j类时,uij=1.通过最小化代价函数,可以得到 k类聚类中心.对于 HRTF而言,聚类中心为 k列 HRTF,由于 HRTF数据中列与声源的方位是一一对应的,因此,若将聚类中心作为特征 HRTF,则其对应的声源方位称为特征方位.

3.2 插值算法

利用聚类算法可从 HRTF数据库中得到具有代表性的特征 HRTF,其余的 HRTF可以通过对特征HRTF插值进行重构得到.这样只需存储特征 HRTF数据,就可以完成对全部 HRTF数据的重构,从而有效地减少了需要存储的数据量.

从前面的分析可知,某一方位的 HRTF可以表示成邻近方位数据的线性加权和形式,这是由HRTF数据间的内在关系所决定的.

改进后的插值算法,可分为以下两步.

(1)线性内插,即直接由特征 HRTF对其余方位的 HRTF作线性内插.

(2)对插值后数据进行修正.

For i=1∶N

从 H读取 Xi对应的最邻近向量;

从W读取相应的权值W(:,i);

For j=1∶d

利用 Xi=∑jW(j,i)X(:,H(j))进行修正;

End

End

修正后的插值方法充分利用了 HRTF数据间的内在关系,插值效果较好.

4 仿真结果

仿真实验数据采用加州大学戴维斯分校图像处理和计算中心所提供的 HRTF数据库[11].该数据库包括 45种耳廓,每个耳廓有 1 250个采样位置,其中水平位置 50个,垂直角 25个,采样频率为 44.1 kHz.每个 HRIR长度为 200个点,采样时间为 4.5 ms.垂直角从 -45.000°～230.625°等间隔分布 ,间隔为 5.625°.水平角从 -80°～80°等间隔分布 ,间隔为 5°.本研究的仿真实验均是在 3#耳廓对应的HRTF数据库下完成的.

4.1 流形

通过数据降维,可以发现数据与主要因素之间的关系[12].当测试声源的水平方位与垂直方位固定时,每个 HRTF就有 N个采样点的序列,在 N维空间中,该序列可以视为一点.当垂直角连续变化时,将其在N维空间中描绘出的一维曲线称为流形,该曲线反映的是垂直方位角与 HRTF之间的关系.流形中包含着垂直方位信息.

本实验考虑在垂直面上θ=0°的情形.利用LLE将 HRTF数据库降成一维,即只保留垂直方位角,一维流形如图 4所示.对于 HRTF数据库,垂直方位角差距较大的 HRTF的欧氏距离可能会很接近.但垂直方位相差越远,流形距离越远,越能较好地区别声源垂直方位上的差异.从图中可以看到,虽然垂直角是均匀间隔的,但所形成的流形距离并非均匀变化,即流形曲线为非线性的.而从局部来看,数据之间又呈现出线性特点,因此,流形是由若干个局部线性的小曲线连续联接而成的.

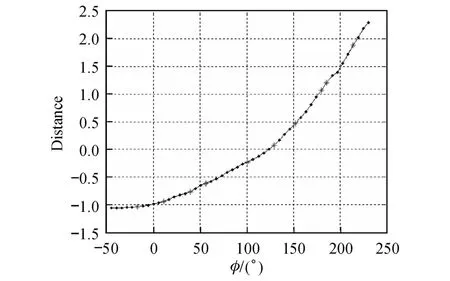
图 4 一维流形与特征角度Fig.4 One d imensionalman ifold and representative angles

4.2 LL E和 PCA算法比较

在 LLE算法中,有 2个参数需要设定:最近邻向量个数 K和维数 d.在仿真实验中,设 K=3,d=6,同时给出利用 PCA进行数据恢复的结果.PCA中主分量的个数选取为 6,其特征值之和占总特征值之和的 95.61%.图 5所示为使用 2种降维方法的数据恢复后的 HRTF与测量得到的 HRTF的比较 (θ=0°,φ =0°),其中 LLE数据恢复利用了 HRTF之间的邻近关系.从图中可以看出,在低频段,2种算法的重构效果基本一致,但在高频段,LLE算法的重构效果好于 PCA算法,这是因为 PCA算法中丢弃的那部分分量与声源的高频有关,即与头部、肩膀、衣服的散射作用有关.

图 5 PCA,LL E数据恢复与测量之间的比较(θ=0°,φ =0°)Fig.5 Data compar ision w ith PCA,LL E and measurement(θ=0°,φ =0°)

归一化误差定义为

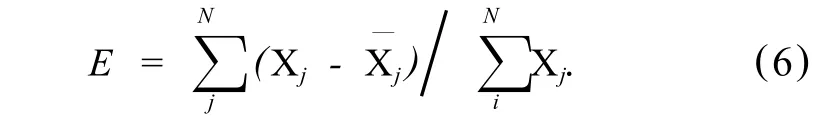
图 6为 PCA和 LLE重构归一化误差.可以看到,基于 LLE的数据恢复的误差总体上小于基于PCA的数据恢复误差.但是在垂直角为 -45°时,LLE的数据恢复误差大于 PCA,原因在于 LLE算法是利用最邻近垂直方位的 HRTF的线性加权和进行数据恢复,一般在该垂直方位的左右两边选择最邻近垂直方位,而 -45°是垂直方位的起始角,在寻找对应的最邻近垂直方位时会出现比较大的误差.但总体而言,非线性流形学习算法比传统线性降维算法的优越性表现在:①无需设置过多的参数;②LLE算法是基于流形的内在几何性质,能发现数据间的内在联系,降维后的数据可保留更多与感知有关的信息,数据恢复误差小;③避免了 PCA算法中的奇异值分解.

图 6 PCA和 LL E重构归一化误差Fig.6 Normalized recon structive error s between PCA and LL E

4.3 特征 HRTF及重构

LLE算法将高维数据降成低维数据,保留了更多感知信息.从低维数据中聚类出特征 HRTF.为了表述方便,特征 HRTF用对应的特征方位表示.经过多次实验得出,分类个数大于 10时可以获得较好的插值重构.此处选取θ=0°的一组数据,选择分类数为 10,聚类中心由对应的特征方位表示,结果为 0°,39.375°,67.500°,95.625°,123.750°,157.500°,180.000°,191.250°,208.125°,225.000°.特征方位在图 4中用“＊”标出.

利用 HRTF进行虚拟声源模拟时,只需在计算机中存储上述特征方位所对应的 HRTF,其余的HRTF可以通过特征 HRTF插值得到.图 7给出了线性内插法重构波形、修正后的插值重构波形与测量值的比较.测量的 HRTF对应方位为θ=0°,φ=0°.线性插值方法直接在 Matlab中实现,所使用的类型为“linear”,调用函数“interp1”实现.

图 7 插值重构比较Fig.7 Reconstruction compar isons w ith interpolation,m od if ied in terpolation and m easurem en t

为了进一步衡量各角度的插值效果,图 8给出了各垂直方位角对应的 HRTF的误差比较.可以看出,由于改进的插值算法充分利用了数据间的内在关系,重构后的效果整体上比直接使用插值算法的效果要好.

总体误差定义为

图 8 全方位插值重构误差比较Fig.8 Reconstruction error compar isons in azim uth

式中,Aj为比较数据,Mj为测量数据.直接内插以及改进后插值的总体误差如表1所示.改进后的插值总体误差比直接线性内插减少了近 4 dB.

表1 总体误差Table 1 Total error

5 结 束 语

本研究在分析 HRTF数据的特征后,将人脸识别中非线性降维算法引入到空间听觉中.与传统的线性降维方法相比,降维后的数据保留了更多的感知信息,有利于数据的聚类.并在此基础上,针对虚拟声源合成的实时性问题,提出了一种基于非线性流形学习的空间听觉重建方法.降维后的数据利用聚类算法聚出 k个中心,即特征 HRTF,其余的HRTF可根据特征 HRTF进行插值重构.在插值过程中,利用数据间的关系对插值过程进行修正,使得重构结果更接近于真实值.实验结果表明,该方法能有效地减少 HRTF的存储数据量,有利于提高虚拟声源合成的效率.

[1] BLAUERT J P.Spatial hearing[M].Massachusetts:M IT Press,1997.

[2] ZOTKIN.Rendering localized spatial audio in a virtual auditory space[J]. IEEE Transaction on Multimedia.2004,6(4):553-564.

[3] HACHHABIBOGLU H,MURTAGH F.Perception based simp lification for binaural room auralization [C]∥Proceeding of the International Conference on Auditory Display.2006:268-271.

[4] HUANG Q H,FANG Y. Interpolation of head-related transfer functions using spherical Fourier expansion[J].Journal of Electronics(China),2009,26(4):571-576.

[5] HUANGQ H,ZHUANGQ L.HRIR personalization using support vector regression in independent feature space[J].Electronics Letters,2009,45(19):1002-1003.

[6] SHIMADA S,HAYASHIS.A clusteringmethod for sound localization transfer functions[J].Journal of the Audio Engineering Society,1994,42:577-583.

[7] HUANG Q H,FANG Y.Modeling personalized headrelated impulse response using support vector regression[J].Journal of Shanghai University:English Edition,2009,13(6):428-432.

[8] ROWERS S, SAUL L. Non-linear dimensionality reduction by locally linear embedding[J]. Science,2000,290:2323-2326.

[9] KAPROLOS B,MEKUZ N,KOPINSKA A,et al.Dimensionality reduced HRTFs:a comparative study[C]∥ Proceedings of Advances in Computer Entertainment Technology.2008:59-62.

[10] SEUNG H S,LEE D D.Themanifold waysof percep tion[J].Science,2000,290:2268-2269.

[11] ALGAZIV R,DUDA RO,THOMOSON DM.The CIPIC HRTF database[C]∥Proc 2001 IEEE Workshop on Applications of Signal Processing to Audio and Acoustics.2001:99-102.

[12] DURA IWWAM I R,RAYKAR V C.The manifolds of spatial hearing [C]∥ Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing.2005:285-288.

Recon struction of Spatial Hear ing Based on L ocally L inear Em bedd ing

TANG Yong-qing1,2, FANG Yong1, HUANGQing-hua1
(1.School of Communication and Information Engineering,Shanghai University,Shanghai200072,China;2.School of Computer and Information Engineering,LishuiUniversity,Lishui 323000,Zhejiang,China)

In spatial hearing,massdata of head-related transfer function(HRTF)isa factor that greatly influences the synthesis of virtual sounds. To reduce the data used,we propose a spatial hearing reconstruction method based on locally linear embedding(LLE).Using LLE,high dimensionality is mapped to a lower dimensional dataset suitable for regressive analysisand classification.To classify by an unsupervised cluster method,a representative HRTF is extracted from all HRTFs.Other HRTFs can be reconstructed in spatial hearing from the representative HRTF with modified interpolation.Compared to the p rincipal component analysis(PCA),the data w ith reduced dimension obtained by using LLE preservemoreperceptive information.Relationsamong the HRTF data can be found,withwhichmodified interpolation can be obtained and HRTF reconstruction error can be reduced.Simulation results show that the proposed method effectively reduces HRTF data. It is useful to imp rove efficiency of synthesis for virtual sound source in practical applications.

head-related transfer function(HRTF);locally linear embedding(LLE);manifold;spatial hearing reconstruction

TN 911.7

A

1007-2861(2011)02-0119-06

10.3969/j.issn.1007-2861.2011.02.003

2010-04-20

国家自然科学基金资助项目 (61001160);上海市自然科学基金资助项目 (08ZR1408300);上海市重点学科建设资助项目(S30108);上海市科委重点实验室资助项目(08DZ2231100)

方 勇 (1964～),男,教授,博士生导师,博士,研究方向为盲信号处理、通信信号处理等.E-mail:yfang@staff.shu.edu.cn

(编辑:赵 宇 )