基于四次谐波选择法的磁通门传感器分析*

李菊萍，刘诗斌，郭 博，刘雨鑫

(西北工业大学电子信息学院，西安 710072)

磁通门传感器(简称磁通门)是一种用于测量微弱磁场(如地磁场)的传感器。与其它类型测磁仪器相比，磁通门传感器具有分辨率高，测量弱磁场范围宽，噪音低，可靠、简易、经济、耐用，能够直接测量磁场的分量和适于在高速运动系统中使用等特点，尤其具有高温下稳定性好的优点，能够满足高温条件下的作业要求，是综合性能最好的磁场测量传感器，因而近些年来成为研究的重点。磁通门已广泛应用于地质探矿、工业探伤、车辆控制、搜查武器以及飞机、卫星、船舰和车辆导航等许多领域。在各种空间计划中，磁场测量往往是整个空间计划中的一个重要组成部分，国际上已将高精度磁通门磁力计作为荷载(Fluxgate Sensor Magnetometer，FGM)在空间卫星上搭载。

磁通门铁芯的磁感应强度与磁场强度是非线性的，在交变磁场的饱和激励下，外磁场对输出信号产生某些非对称的调制作用，磁通门测磁法的物理实质是通过检测输出信号中的这些非对称的变化来测量弱磁场的［1－2］。被测磁场可以通过检测输出信号迟滞时间差而得到［3－5］，为了解决线圈匝数增大而带来传感器体积增大和动态性能差的问题，还出现了检测输出电流的电流输出型磁通门传感器［6－7］。大多数磁通门都是通过检测其输出信号的二次谐波幅度来测量磁场的［8－12］，文献［13］比较了四次谐波和二次谐波，结果显示在外磁场较小时适合采用四次谐波选择法。文献［13］采用反正切函数，并未考虑矫顽力对四次谐波和二次谐波的影响。本文采用分段折线近似磁滞回线，从理论上研究了磁滞回线形状对四次谐波和二次谐波的影响，详细分析了四次谐波的适用条件。

1 磁通门工作原理

为方便分析考虑矫顽力对磁通门输出的影响，假设铁心的B－H磁滞回线近似为折线形状，如图1。Hk为饱和磁场强度，当|H|＜Hk时，铁芯的相对磁导率近似为Ms/(Hk－Hc);当|H|＞Hk时，铁芯达到饱和。

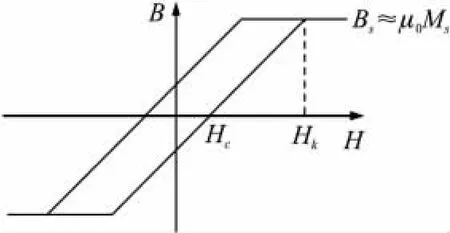
图1 磁滞回线简化为分段折线

检测线圈中的感应电动势ε在一个周期内可表示为:

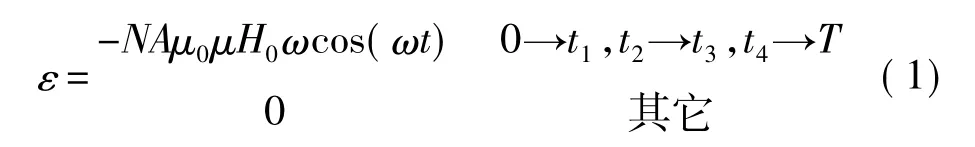
其中A为磁芯的横截面积，N为感应线圈的匝数，μ≈Ms/(Hk－Hc)为磁芯的相对磁导率，μ0为真空磁导率。

t1、t2、t3、t4满足以下关系:

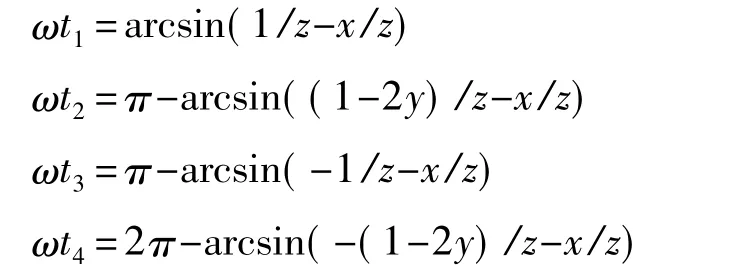
其中x=Ha/Hk，y=Hc/Hk，z=H0/Hk，Hc为矫顽力，Ha为被测磁场，H0为激励磁场幅值。

外磁场在铁芯中形成的磁通被交变磁场所调制，直流外磁场在一半周期内使铁芯提前达到饱和，而在另外半个周期内使铁芯推迟饱和。激励周期内正负半周不对称，为了消除变压器效应的影响，通常采用两个单铁心磁通门将初级线圈反接构成双铁心磁通门，两次级线圈顺接，从而使输出电压曲线中出现偶次谐波。采用谐波选择法将磁通门信号提取出来，感应电动势各偶次谐波的实部幅值为:

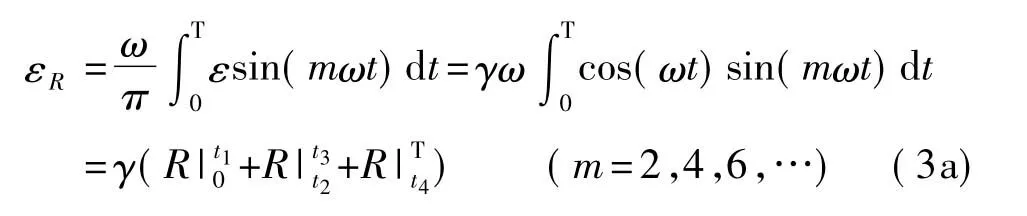
电动势各偶次谐波的虚部幅值为:

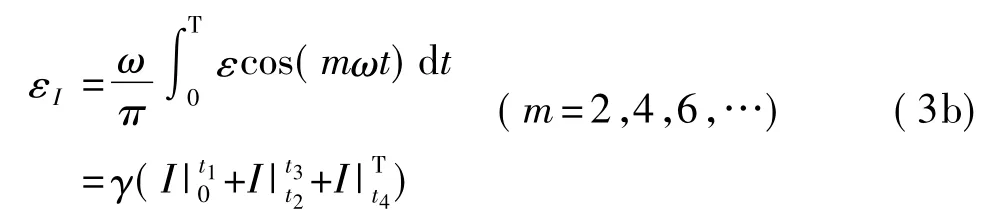
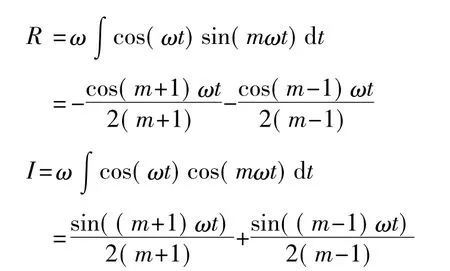
各偶次谐波幅值为

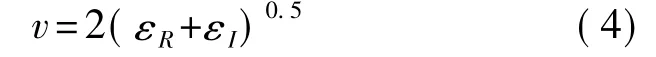
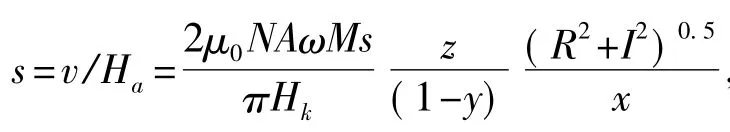
2 二次谐波法与四次谐波法比较

2.1 灵敏度分析比较

磁滞回线近似为三段折线［1－2］不考虑矫顽力时，二次谐波灵敏度在激励磁场幅值与与饱和磁场比值为时达到最大。考虑矫顽力后磁滞回线近似为图1，图2为二次谐波灵敏度(m=2)与比值y的关系，曲线 a、b、c、d、e、f对应比值z分别为 1.05、1.2、1.4、1.8、2、2.5。随着矫顽力与饱和磁场强度比值y增大，二次谐波灵敏度增大，当比值y较小时，随着激励磁场幅值与饱和磁场比值z增大，灵敏度先增大后减小，当比值y较大时，随着激励磁场幅值与饱和磁场比值z增大，灵敏度减小。当激励磁场幅值与饱和磁场比值z较大时，灵敏度随比值y变化不大。

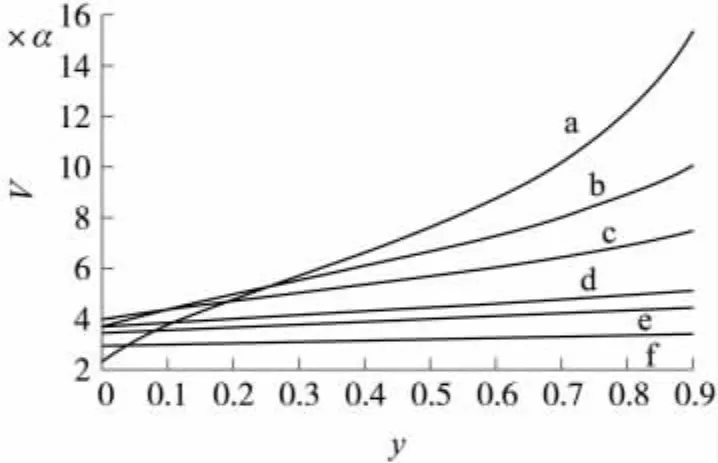
图2 二次谐波灵敏度(m=2)同矫顽力与饱和磁场比值 y的关系，α=2μ0NAωMs/(πHk)

图3为二次谐波(m=2)与四次谐波(m=4)的灵敏度比值同比值y的关系。曲线 a、b、c、d、e、f、g、h、i、j、k、l对应激励磁场幅值与饱和磁场比值z分别为1.01、1.05、1.1、1.2、1.3、1.4、1.6、1.8、2、2.5、3、4。由图3可得:当比值z大约大于2时，不论矫顽力与饱和磁场强度多大，四次谐波灵敏度大于二次谐波灵敏度，且随着比值y增大，四次谐波灵敏度与二次谐波灵敏度比值增大。比值z大约小于时，随着矫顽力与饱和磁场度比值y增大，四次谐波灵敏度与二次谐波灵敏度比值先减小后增大。

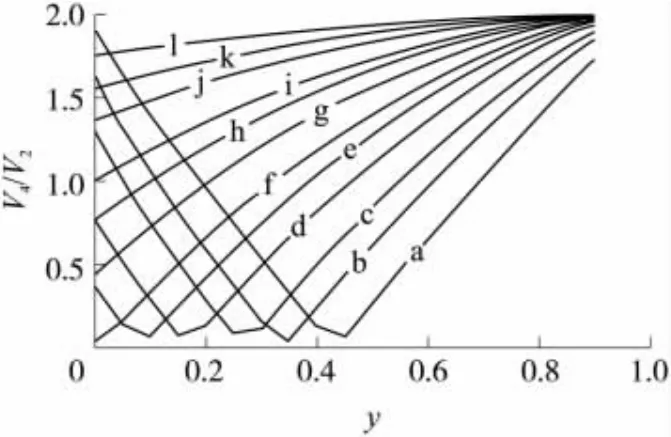
图3 二次谐波(m=2)与四次谐波(m=4)的灵敏度比值同比值y的关系，y为矫顽力与饱和磁场强度比值。

与文献［13］比较，文献［13］采用反正切函数，忽略矫顽力，只分析了激励磁场幅值较大时，四次谐波灵敏度大于二次谐波灵敏度的情况。采用分段折线考虑矫顽力，从图2和图3分析可得选取四次谐波还是选取二次谐波，不仅取决于比值z，还取决于y。由图2可得，当不考虑矫顽力，二次谐波在激励磁场与饱和磁场比值为时达到最大值。这与文献［1－2］结果一致。由图3可得，尽管激励磁场与饱和磁场比值为时二次谐波达到最大，矫顽力与饱和磁场比值大约大于0.35时，应考虑使用四次谐波。

考虑两个极端情况，当矫顽力与饱和磁场比值y较小，而且激励磁场幅值较小时四次谐波幅值大于二次谐波幅值，随着激励磁场幅值增大，二次谐波幅值先增大后减小，四次谐波幅值先减小后增大，最后四次谐波幅值大于二次谐波幅值。当矫顽力与饱和磁场比值y较大，适合四次谐波法，而且激励磁场幅值越小，灵敏度越大。若要确保深度饱和激励以消除剩磁［14］，应采用四次谐波法。

2.2 线性范围和非线性误差比较

表1为线性范围和非线性误差随矫顽力与饱和磁场强度比值y，激励磁场与饱和磁场强度比值z的变化关系。δ2(δ4)为二次(四次)谐波误差，被测磁场为x×Hk，激励磁场为z×Hk，Hk为饱和磁场。

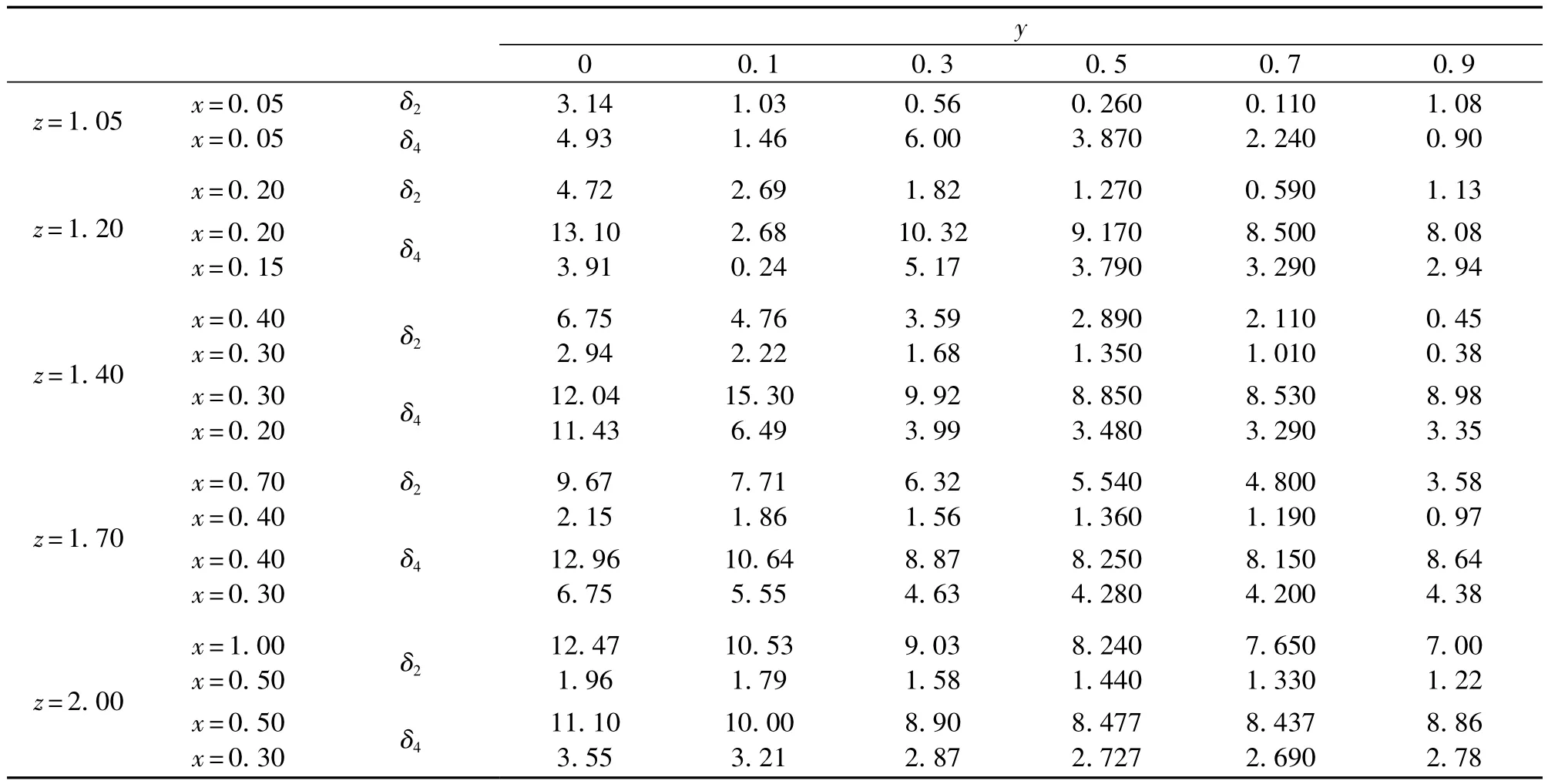
表1

由表1可得四次谐波小于二次谐波线性范围，随着激励磁场幅值与饱和磁场比值z增大，线性范围增大，而且四次谐波与二次谐波线性范围差距变大。由表1(z=1.05)可得激励磁场幅值较小且矫顽力较小时，虽然四次谐波大于二次谐波灵敏度，但量程很小。

比值z大约大于1.4时，随着矫顽力与饱和磁场强度比值y增大，二次谐波非线性误差单调减小，四次谐波非线性误差先急剧减小再增大，但是增大幅值很小。比值小于1.4时，非线性误差随矫顽力与饱和磁场强度比值y变化不单调。随比值y增大，二次谐波非线性误差先减小后增大，且增大幅值很小。四次谐波非线性误差在y小于0.3内波动较大。

3 结束语

传统磁通门采用二次谐波法，文献［13］用反正切函数近似磁滞回线，提出采用四次谐波选择法。本文采用分段折线近似磁滞回线，通过理论推导得到各偶次谐波灵敏度解析表达式。详细比较了二次谐波选择法和四次谐波选择法灵敏度，量程和非线性度。研究结果表明选取四次谐波还是选取二次谐波，不仅取决于激励磁场幅值与饱和磁场强度比值，还取决于矫顽力与饱和磁场强度比值。

［1］刘诗斌.微型智能磁航向系统研究［D］.［博士学位论文］.西安:西北工业大学，2001.

［2］张学孚，陆怡良.磁通门技术［M］.北京:国防工业出版社，1995，30－49.

［3］Andò B，Baglio S，Bulsara A R，et al.Design and Characterization of a Microwire Fluxgate Magnetometer［J］.Sensors and Actuators A，2009，151(2):145－153.

［4］Dari A，Bosi L，Gammaitoni L，et al.Nonlinear Sensors:An Approach to the Residence Time Detection Strategy［J］.Phys.Rev.E，2010，81:011115.

［5］Ando B，Baglio S，Sacco V，et al.PCB Fluxgate Magnetometers with a Residence Times Difference Readout Strategy:The Effects of Noise［J］.IEEE Transactions on Instrumentation and Measurement，2008，57(1):19－24.

［6］Primdahl F，Ripka P，Petersen J R，et al.The Sensitivity Parameters of the Short-Circuited Fluxgate［J］.Meas.Sci.Technol，1991，2:1039－1045.

［7］刘诗斌，段哲民，严家明.电流输出型磁通门传感器的灵敏度［J］.仪表技术与传感器，2002，4－6.

［8］Huang Weng Sheng，Jeng Jen-Tzong，Lu Chih-Cheng.Harmonic Frequency Characterisations of a CMOS Micro Fluxgate Sensor for Low Magnetic Field Detection［J］.Procedia Engineering，2010，5:993－996.

［9］刘石，李宝清，童官军，等.一种平面四轴向磁通门传感器的设计［J］.传感技术学报，2010，23(11):1565－1569.

［10］Baschirotto A，Dallago E，Malcovati P，et al.An Integrated Micro-Fluxgate Magnetic Sensor with Front-End Circuitry［J］.IEEE Transactions on Instrumentation and Measurement，2009，58(9):3269－3275.

［11］Baschirotto A，Dallago E，Malcovati P，et al.A Fluxgate Magnetic Sensor:From PCB to Micro-Integrated Technology［J］.IEEE Transactions on Instrumentation and Measurement，2007，56(1):25－31.

［12］Janosek M，Ripka P.PCB Sensors in Fluxgate Magnetometer with Controlled Excitation［J］.Sensors and Actuators A，2009，151:141－144.

［13］Trujillo H，Cruz J，Rivero M，et al.Analysis of the Fluxgate Response Through a Simple Spice Model［J］.Sensors and Actuators，1999，75:1－7.

［14］刘诗斌，崔智军，刘昭元.低剩磁误差磁通门的激励电路研究［J］.传感技术学报，2009，22(12):1709－1712.