一种基于Graph Cuts的多尺度乳腺肿块分割方法*
吴相颖,徐伟栋,厉力华*,刘 伟,张 娟,邵国良,Zheng Bin
(1.杭州电子科技大学生命信息与仪器工程学院,杭州 310018; 2.浙江省肿瘤医院放射科,杭州 310022; 3.匹兹堡大学放射学系,宾夕法尼亚州 15213,美国)
乳腺癌是当今女性最常见的恶性肿瘤之一。乳腺X线摄影是目前乳腺癌最常用和最有效的诊断手段之一[1-2]。然而,由于乳腺组织的复杂性及有限的分辨率等原因,乳腺X线图像往往不够清晰,加上人的视觉感知等主观因素,临床医生在阅片时容易出现漏检或诊断错误。为了帮助医生更好地诊断病情,乳腺钼靶计算机辅助诊断技术(Computer Aided Diagnosis,CAD)成为了目前国际上的研究热点。
肿块分割作为肿块检测和诊断的关键环节,是CAD的一个研究热点,许多学者做了大量的工作[3-6]。然而由于乳腺图像中噪声、伪影较多,肿块形状和背景复杂多变,现有方法的分割结果往往不够理想。
基于Graph Cuts理论[7]的图像分割技术最早来源于组合优化理论。该算法基本过程为:首先分别选定部分图像像素作为目标和背景,然后以像素作为节点,以像素之间的相邻关系作为边,构造一个图(Graph),最后运用最大流/最小割算法对网络进行切割,得到的最小割对应于待分割的目标边界。Graph Cuts算法具有全局最优求解能力及结合多种知识的统一图像分割框架,引起了研究者越来越多的关注,在乳腺肿块分割方面也有所应用[8-9]。但是,海量的节点及为达到一定分割精度而采用的迭代求解模式,使得大多数基于Graph Cuts的分割算法耗时较大。当临床医生手动选定的目标和背景像素较少时,在目标和背景的边界容易出现一些像素被错误划分情况。另外,大量交互操作加重了临床医生工作量,降低了分割速度,不适合进行批量图像分割处理。
Rother等人[10]对交互式 Graph Cuts算法进行改进,提出了GrabCut算法。它进一步简化了交互操作,用户只需要选定一个矩形框包含整个目标,将框外的像素作为背景,利用Graph Cuts进行多次迭代,得到对象和背景的分割结果。然而由于乳腺组织和病灶的复杂性,乳腺图像中乳房组织和病灶区域的灰度通常是不均匀的,这使得传统Graph Cuts算法以及GrabCut算法在分割乳腺肿块图像时结果往往并不理想。
针对乳腺图像的这些特点,本文提出一种基于Graph Cuts算法的多尺度乳腺肿块自动分割方法。首先,采用区域统计融合方法对图像进行粗分割,将得到的粗轮廓替代传统Graph Cuts算法中的手动标记,并作为后续Graph Cuts分割的初始轮廓。在迭代优化阶段,本文引入多尺度分析方法,以高斯金字塔分解得到的多尺度图像序列代替固定尺度的原始图像序列估计GMM参数,将粗糙尺度的易分割性与精细尺度的精确性互补,使得算法快速确定GMM参数以执行Graph Cuts分割。考虑到传统Graph Cuts算法处理海量的节点耗时较大,通过分水岭变换将图像划分成若干内部连通且有良好边缘的小区域块,将区域块内像素灰度的均值作为块内每个像素的灰度强度以提高算法的抗噪能力,从而以较少的分块替代海量的像素进行分割。
本文第2部分介绍基于Graph Cuts算法的多尺度图像分割方法,第3部分对提出的方法进行实验验证,并与交互式Graph Cuts算法和GrabCut算法进行了实验对比,最后给出本文的结论。
1 方法
1.1 传统交互式Graph Cuts算法
图像分割问题是一个将像素标为目标/背景的典型二元标号组合优化问题。Graph Cuts理论的核心思想在于构造一个能量函数,然后运用组合优化技术最小化该能量函数。通过构造网络、最小化能量函数及网络流理论,可以把标号问题转换为用最大流/最小割方法[11]来解决。
设G=(V,E)为一无向图,在边集X上定义容量函数c:E→R+,称图G及其边集E上的容量函数c构成了一个s-t网络,记作N=(G,s,t,c),其中,s和t分别称为网络的源点和汇点。定义t-link为图G中连接节点与s或t的边。通过最小化Gibbs能量函数E(f),把顶点集V划分为分别与源点s和汇点t相连的两个顶点集S,T(s∈S,t∈T)。

式中:f为V的一个标号,f:P→L(L∈{“obj”,“bkg”})。R(f)只与像素的灰度有关,称为数据能量项;B(f)只跟邻域标号相关,称为平滑能量项。系数λ≥0,指定了数据能量项与平滑能量项的相对重要性。
图1是我们使用传统交互式Graph Cuts算法对一幅乳腺图像ROI分割的结果。图1(a)为手动标记操作。其中,肿块内部标记代表目标种子点,肿块外部标记代表背景种子点。图1(b)为传统Graph Cuts分割结果。式(1)中的数据能量项R(f)和平滑能量项B(f)分别通过下面公式计算:

图1 传统交互式Graph Cuts算法的分割结果

如图1(b)所示,无论是肿块内部还是周围区域,灰度分布都不均匀,Graph Cuts算法虽然可以大致地分割出肿块轮廓,但对肿块边缘细节分割并不理想,如图1(b)肿块的边缘区域A并没有得到很好分割。
1.2 基于Graph Cuts的多尺度乳腺肿块自动分割方法
针对乳腺图像分割问题,无论是肿块内部还是周围区域,灰度分布都不均匀,Graph Cuts算法虽然可以大致地分割出肿块轮廓,但对肿块边缘细节分割并不理想。另外,大量交互操作加重了临床医生工作量,不适合进行批量图像分割处理。因此,本文提出一种基于Graph Cuts算法的多尺度乳腺肿块自动分割方法。
本文提出的方法概述如图2所示。首先,应用统计区域融合方法对乳腺图像进行粗分割,并将获得的粗轮廓替代手动标记的“目标”和“背景”种子点。通过实验测定平滑参数σ的初值,并将σ按照公式 σ=α·σ(0<α<1)更新。迭代 Graph Cuts算法进行分割,对每一次 Graph Cuts分割结果,通过GMM建立目标类和背景类的灰度分布模型,然后利用目标类和背景类的距离变换更新先验概率。结合先验概率和GMMs计算后验概率,并将其值赋予下一次Graph Cuts处理中的t-link。为了提高算法的分割速度,采用分水岭算法将图像划分成若干内部连通且有良好边缘的小区域块,并以较少的分块替代海量的像素进行Graph Cuts分割。通过多次实验经验可知,σ和α分别设置为2和0.6,迭代的次数为4次左右时就能取得较满意的结果。

图2 本文提出的方法概图
1.2.1 区域统计融合
区域统计融合[12](Statistical Region Merging,SRM)是一种线性时间快速、简单的区域增长图像分割算法。它基于自适应统计阈值,在灰度通道上合并而不需要保持动态区域邻接图的谓词。该算法分两步:①点对排序,将图像按照四邻接两两结合结成点对,选择一个函数计算点对的融合代价,并按照融合代价的大小进行排序;②按照下式对排序结果进行图像融合:

式中:R为区域中像素个数,b(R)为融合参数,δ为图像总像素个数倒数的1/6,Q是质量因子,Q越大分割越细致。从实验的角度来看,调整Q的值修改事件的统计复杂性,然后构建由粗到细(多尺度)分割图像的层次结构,从而有可能控制分割的粗糙度。
通过SRM算法的处理,可以将图像中纹理相同的像素融合为一个区域,完成对乳腺图像的粗分割。同时提取分割结果的轮廓,替代传统Graph Cuts算法中的手动标记,并作为后续Graph Cuts分割的初始轮廓。如图3所示是一幅乳腺图像SRM粗分割结果,图3(b)为SRM分割结果。不同的色块代表不同的区域,其中的灰度是取自色块所在区域的原始图像像素的灰度均值。图3(c)为我们提取的粗分割图像,并为后续分割提供初始轮廓。

图3 SRM分割结果
1.2.2 高斯金字塔模型
考虑到乳腺图像的灰度非均匀性和Graph Cuts算法本身局限性,我们引入多尺度分析[13]提高肿块分割精度。
高斯金字塔[14]是一种经典的多分辨率空间图像分析方法。定义I为原始图像,G(σ)为高斯核函数。则平滑图像L(σ)由下式给出:

注意到,如果高斯参数σ很大,我们需要增大窗口的尺寸来适应高斯滤波器,这在实际设计中存在很大困难,因此我们采用下采样处理来获取平滑图像。特征为图像尺寸随着尺度水平的增加呈指数下降,粗尺度图像是细尺度图像的子集,不同尺度间图像的像素在位置上仍保持着相应的几何拓扑关系。
塔式分解n-1次后所得由粗至细的多尺度图像序列为f(n-1),f(n-2),…,f(1),以该图像序列代替固定尺度的原始图像序列来迭代分割获取目标/背景样本点。由于GMM参数估计是一个由粗至细、逐步求精的逼近过程,虽然最初的图像尺寸较粗,对应的样本容量较小,但并不影响对GMM参数的粗略估计,随着迭代估计的进行,样本容量也随之增大,满足了对GMM参数进一步准确估计的要求。塔式分解把精细尺度的精确性与粗糙尺度的易分割性两者有机地统一起来,从而使得GMM参数估计过程更为快速有效。我们通过使用不同标准差值对原始图像进行高斯滤波,之后迭代Graph Cuts算法,实现从全局到局部的逐步分割过程。
1.2.3 分水岭变换
注意到传统Graph Cuts算法是通过建立像素级的马尔可夫随机场(MRF)模型[15]实现分割,对于较大尺寸的乳腺肿块图像而言,海量的节点使得Graph Cuts处理耗时较大。因此本文采用分水岭算法作为预处理将图像划分成若干个内部连通且具有良好边缘的小区域块,然后将区域块内像素灰度均值作为块内每个像素的灰度强度以提高算法的抗噪能力。在执行Graph Cuts阶段,用区域块替代像素作为新的节点进行分割,提高算法的运行效率[16]。
图4所示为经过分水岭算法分割产生的一个邻域结构,每个节点代表一个区域块,节点之间有边相连接表示这两个节点互为邻域。图4(a)是分水岭过分割得到的6个区域块,图4(b)的邻域结构是通过将拥有共同边界的区域块设为邻域而建立的,这种邻域结构在乳腺肿块图像分割的实验中被证明有效。
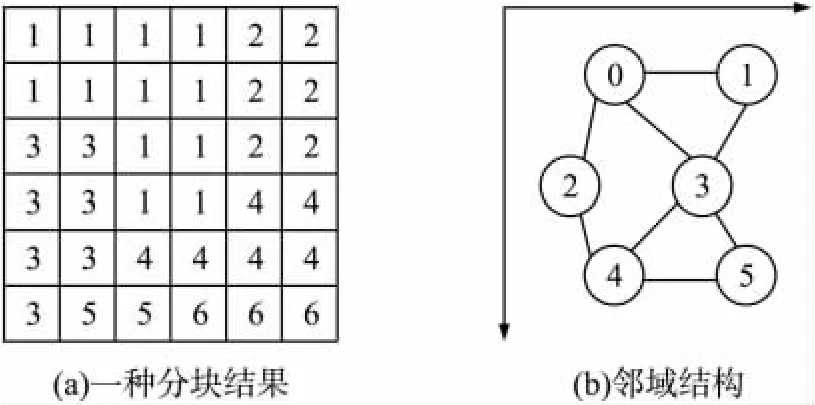
图4 分水岭分割产生的分块结果及对应的邻域结构
1.2.4 迭代优化与参数估计
根据前一次Graph Cuts分割结果的距离变换和灰度直方图的可能性,计算先验概率,并按照下面两式将其值赋予下一次Graph Cuts处理中的t-link:


其中,Pr(O|Ip)和Pr(B|Ip)由下面公式给出:
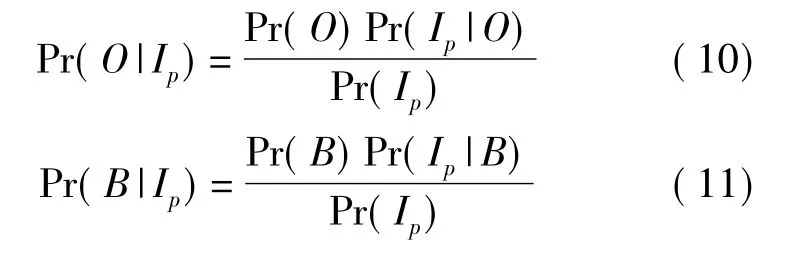
Pr(Ip|O),Pr(Ip|B)和 Pr(O),Pr(B)由前一次Graph Cuts分割结果计算得到。图5所示为根据可能性和先验概率更新t-link。

图5 更新可能性和先验概率
可能性Pr(Ip|O),Pr(Ip|B)由GMM计算得到。GMM由下式获得:

根据前一次Graph Cuts处理结果的空间信息更新先验概率Pr(O),Pr(B)。由于边界附近像素点的下一次分割标号不确定,使用距离变换的结果更新先验概率。节点到边界的距离被归一化到0.5~1范围内。令dobj、dbkg分别为目标点和背景点的距离变换。则先验概率为:

最后,利用GMM得到的Pr(Ip|O),Pr(Ip|B),和距离变换得到的Pr(O),Pr(B),根据式(8)和式(9)计算后验概率。通过前一次Graph Cuts分割结果,我们获取灰度直方图的可能性和距离变换,并计算先验概率,然后将其值赋予下一次Graph Cuts处理中的t-link。
2 实验结果及讨论
2.1 数据集
将本文方法应用于110例包含肿块的乳腺X线图像ROI(Region of Interest)进行肿块分割实验,以验证算法的有效性和优越性。这些图像来自于南佛罗里达大学的DDSM(Digital Dataset for Screening Mammography)数据库,ROI图像灰度均为8位,图像尺寸平均值为709像素×708像素。
2.2 评价方案
为了比较分割方法的性能,我们将本文所提出的多尺度Graph Cuts算法与传统的交互式Graph Cuts算法以及GrabCut算法做了实验对比。
本文方法的参数设置:区域统计融合中质量因子Q的值指定为1,2,4,…,256 范围内,Gibbs能量函数的系数λ设为0.5,高斯平滑参数σ和控制因子α分别设置为2和0.6,迭代的次数为4次。
为定量评价分割的质量,通常的做法是将算法分割得到的结果与该领域专家手动分割的结果进行像素级别的比较。为此,我们邀请了3位乳腺癌诊断研究人员对测试图片进行手动分割,分割的结果作为实验的比较轮廓。本文采用误分率作为实验结果的评价算法,误分率定义为过分割率和欠分割率之和。其中,过分割率和欠分割率的定义如下:

误分率的值越小,表示分割结果越好。当值为0时,表示算法分割结果与手工分割结果一致。
2.3 实验与讨论
将本文方法、交互式Graph Cuts算法以及Grab-Cut算法应用于110例肿块病灶图像,进行分割实验,并对比最终的分割结果。
图6为本文方法与交互式Graph Cuts、GrabCut分割结果的对比。第1列是交互式Graph Cuts的手动标记,其中肿块内部标记代表目标种子点,肿块外部标记代表背景种子点。第2列是相应的分割结果。从图中可以看出,肿块中心的灰度高于肿块边缘,而背景区域也因存在乳腺组织而呈现灰度非均匀性,Graph Cuts分割肿块边缘部分的结果并不理想。另外,交互式Graph Cuts分割需要大量的手动标记操作,因此加重了临床医生的工作量,而且不适合批处理分割。
图6中第3列是GrabCut算法分割的结果。它进一步简化了交互操作,用户只需要选定一个矩形框包含整个目标,将框外的像素作为背景,利用Graph Cuts进行多次迭代,得到乳腺肿块区域的分割结果。但是当初始标记与目标轮廓偏差较大时,该方法容易产生错误的分割结果,如该列的第2个和第3个分割结果。

图6 本文方法与交互式Graph Cuts、GrabCut分割结果的对比
图6第4列是本文方法的分割结果。通过结合SRM的粗分割和Graph Cuts的精分割,我们的方法实现了乳腺肿块的自动分割。另外,分水岭算法和多尺度分析提高了整体运行效率和分割精度。以图6的第4行为例,左侧图片是交互式Graph Cuts的分割结果,可以看出,当肿块内部灰度分布不均匀时,交互式Graph Cuts算法和GrabCut算法没能准确地分割出肿块边缘,而我们的方法通过对已经比较接近真实轮廓的粗分割结果进行全局优化处理,得到了比较理想的分割结果。
左边第1列为交互式Graph Cuts手动标记操作,第2列为交互式Graph Cuts分割结果,第3列为GrabCut分割结果,最后一列为本文方法分割结果。
表1列出了本文方法和传统方法[7,10]分割结果的误分率(%)。本文方法相比传统交互式Graph Cuts算法获得1.89%更好的分割结果。为了进一步说明3种分割方法之间的差异,根据传统交互式Graph Cuts分割结果,我们定义误分率低于2%的图像为成功分割的图像,误分率超过2%的图像为误分割图像。

表1 交互式Graph Cuts、GrabCut和本文方法分割结果的误分率平均值 单位:%
表2列出了成功分割的图像和误分割图像的误分率(%)。在成功分割图像的误分率方面,本文方法和交互式Graph Cuts方法具有一定的可比性,如图6的第1行和第2行分割结果。但是,在误分割图像方面,本文方法比交互式Graph Cuts方法拥有更好的分割结果,如图6的第3行和第4行分割结果。交互式Graph Cuts算法分割得到的误分割图像的误分率(0.77%)与成功分割图像的误分率(7.21%)相比差异较大,而本文方法通过引入多尺度思想,把Graph Cuts算法及GMM模型结合起来,利用图像的全局和局部信息对肿块进行分割,使得二者差异并不明显,因此本文提出的方法具有较高的稳定性。实验结果表明本文的方法在肿块分割方面要优于交互式Graph Cuts算法和GrabCut算法。

表2 交互式Graph Cuts、GrabCut和本文方法成功分割的图像以及误分割图像的误分率平均值 单位:%
3 结论
本文提出一种基于Graph Cuts的多尺度肿块自动分割方法。首先,应用区域统计融合方法对图像进行粗分割,将得到的粗轮廓作为后续Graph Cuts分割的初始轮廓。在迭代优化阶段,利用高斯金字塔分解得到多尺度图像序列,将粗糙尺度的易分割性与精细尺度的精确性互补,从而以较少样本快速确定GMM参数,以执行Graph Cuts分割。通过结合Graph Cuts算法和多尺度高斯平滑处理,本文提出的方法弥补了交互式Graph Cuts和GrabCut算法在处理肿块边缘细节以及交互处理方面的不足。另外,分水岭算法对图像进行预处理,提高了算法的分割速度及抗噪能力。本文的多尺度分割模型是通过Graph Cuts算法实现的,具有良好的全局最优求解能力,能够较好地处理形状复杂多变的乳腺肿块分割问题。理论分析与实验结果表明,本文的方法在乳腺肿块分割方面具有良好的效果。
[1]Denise Guliato,Rangayyan R M,Carnielli W A.Segmentation of Breast Tumors in Mammograms by Fuzzy Region Growing[J].IEEE Engineering in Medicine and Biology Society,1998,20(2):10022-10051.
[2]Cai Xiaopeng,Chen Xiaowei,Hu Liming,et al.Computer-Aided Detection and Classification of Mieroealeifieations in Mammograms:A Survey[J].Pattern Recognition,2003,36(12):2967-2991.
[3]Chang Y H,Hardesty L A,Harim C M,et al.Knowledge-Based Computer-Aided Detection of Masses on Digitized Mammograms:A Preliminary Assessment[J].Med.Phys,2001,28(4):455-461.
[4]Sheila Timp,Nico Karssemeijer.A New 2D Segmentation Method Based on Dynamic Programming Applied to Computer Aided Detection in Mammography[J].Med.Phys,2004,31(5):958-971.
[5]Camilus K S,Govindan V K,Sathidevi P S[J].Computer-Aided I-dentification of the Pectoral Muscle in Digitized Mammograms[J].Journal of digital imaging,2009:1-19.
[6]Zou Fengmei,Zheng Yufeng,Zhou Zhengdong,et al.Gradient Vector Flow Field and Mass Region Extraction in Digital Mammograms[C]//21st IEEE International Symposium on Computer-Based Medical Systems,pp.41-43,2008.
[7]Boykov Y,Jolly M P.Interactive Graph Cuts for Optimal Boundary& RegionSegmentationofObjectsin N-D Images[C]//Proceedings of the 8th International Conference on Computer Vision,Vancouver,Canada,1:105-112,2001.
[8]Saidin N,Ngah U K,Sakim H A M,et al.Density Based Breast Segmentation for Mammograms Using Graph Cut Techniques[C]//TENCON(IEEE Region 10 Conf.),2009,pp.1-5,doi:10.1109/TENCON.2009.5396042.
[9]Nafiza Saidin,Umi Kalthum Ngah,Harsa Amylia Mat Sakim,et al.Density Based Breast Segmentation for Mammograms Using Graph Cut and Seed Based Region Growing Techniques[C]//Second International Conference on Computer Research and Development,pp.246-250,2010.
[10]RotherC,Kolmogorov V,BLAKE A.GrabCut:Interactive Foreground Extraction Using Iterated Graph Cuts[C]//Proceeding of the 2004 SIGGRAPH Conference,Aug 2004,I;309-314.
[11]Boykov Y,Kolmogorov V.An Experimental Comparison of Min-Cut/Max-Flow Algorithms for Energy Minimization in Vision[C]//IEEE Transactions on Pattern Analysis and Machine Intelligence(PAMI),September,2004.
[12]Richard Nock,Frank Nielsen.Statistical Region Merging[J].IEEE Trans.Pattern Anal.Mach.Intell.,2004,26(11):1452-1458.
[13]Xu Ying,Hong Zhi.Study of Multi-Scale Enhancement Algorithm for THz Images Combining Wavelet Denoising[J].Chinese Journal of Sensors and Actuators,2011,24(3):398-401.
[14]WANG Xun,ZHA Yu-fei,BI Du-yan.Image Segmentation Based on Multi-Resolution Analysis and Watershed Algorithm[J].Opto-Electronic Engineering,2007,34(6):72-76.
[15]Li Xin-wu.Multisource Image Fusion Method Using Markov Random Field Model and EM Algorithm[J].Chinese Journal of Sensors and Actuators,2006,19(2):525-529.
[16]Stawiaski J,Decencière E,Bidault F.Interactive Live Tumor Segmentation Using Graph-Cuts and Watershed[C]//Workshop on 3D Segmentation in the Clinic:A Grand ChallengeⅡ.Liver Tumor Segmentation Challenge.MICCAI,New York,USA,(2008).

