三轴加速度传感器安装误差标定方法研究

张 辉，柴 伟，罗 强，刘漫霞

(中山大学智能交通研究中心，广东省智能交通系统重点实验室，广州 510006)

近年来微机电系统(MEMS)的研究发展迅速，加速度传感器在汽车电子领域的应用日益广泛［1］。在这些应用中，通常需要测量以车辆坐标系为基准的加速度数据，这就需要加速度传感器的各感应轴方向与车辆坐标系一致［2－3］。但是由于安装工艺的影响，在设备安装过程中往往出现加速度传感器感应轴方向与理想的感应轴方向存在误差的情况，这一安装误差对车辆状态数据的测量精度有关键的影响，有必要对这一安装误差进行标定和校准。

在飞机等需要高精度测量的应用中，机载设备安装姿态的传统校准方法都需要利用水准仪、光学经纬仪和激光雷达等精密测量仪器［4］，这些仪器不仅价格比较高，而且操作比较复杂，完成一次校准过程比较耗时耗力，对于低成本的应用不太适合。在捷联惯导系统的各种初始对准方法中，都需要依靠加速度传感器以及陀螺仪测量数据才能完成粗对准［5－6］，而陀螺仪同样价格比较高，维护困难。

为了能够在简易安装的情况下尽量降低安装误差的影响，本文首先对安装误差进行分析和推导，并根据欧拉定理建立了误差标定模型，通过解算传感器自身测量数据来实现安装误差的标定和校准。标定过程不需要借助其他测量仪器，操作简单且成本很低，并通过模拟数据验证了此方法的可靠性。

1 安装误差分析与定义

在安装基于三轴加速度传感器的车辆状态测量设备时，最理想的安装状态是使三轴加速度传感器的三个感应轴分别与车辆坐标系(如图1所示)的三轴平行［7］，此时测量与记录的数据最接近车辆的真实行驶状态。三轴加速度传感器的坐标系在出厂时已标定完成，并认为其三个轴是相互正交的［8］。

实际安装完成后不可能保证传感器的坐标系三轴与车辆坐标系三轴完全平行，将两个坐标系之间的偏差定义为安装误差。为了更直观的描述安装误差，引入旋转矩阵来表示两个坐标系的相对关系，并用欧拉角定义安装误差角度。根据欧拉定理，两个空间直角坐标系可以经过三次绕轴转动后完全重合［9］。传感器坐标系XSYSZS与车辆坐标系XVYVZV的转动关系如图2所示，每次转动的角度即为安装误差角度，并定义绕轴转动的顺时钟方向为正。

图1 车辆坐标系

图2 转动关系

转动过程如下:

三次转动变换矩阵分别为Cφ，Cθ，Cγ，坐标系的转换关系如下:

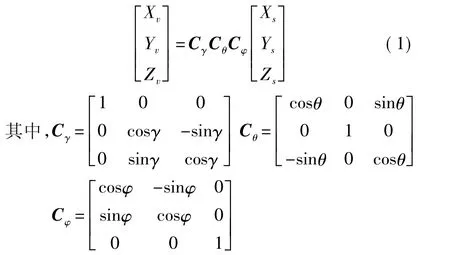
任一空间矢量A在传感器坐标系中的坐标与其在车辆坐标系中的坐标满足以下关系:

式(3)通过矩阵形式表示空间向量在传感器坐标系和车辆坐标系之间的转换关系，系数矩阵中的三个角度φ、θ、γ就是传感器的安装误差角度。只要获得了安装误差角φ、θ、γ，就可以通过式(3)的转换克服安装误差带来的影响，获得车辆坐标系的加速度测量值。

2 安装误差的标定方法

对安装误差的标定即求解三个安装误差角φ、θ、γ。考虑到在静止状态下，加速度传感器仍然会由于重力加速度的原因，在各个轴上感应到相应的加速度数值，同时由于车辆坐标系与地理坐标系之间同样存在着欧拉转动关系，当车辆静止在某一平面上时，通过重力加速度g在坐标系之间的转换关系建立欧拉矩阵方程［11］，与式(3)联立之后就可以建立误差标定模型，从而解算出安装误差角。

2.1 安装误差标定模型

为了推导安装误差的标定模型，首先假设车辆停放在一个平面上，此平面与水平面夹角为α(即坡角)，车头方向与平面最大坡度方向的夹角为β，此时车辆坐标系XVYVZV与地理坐标系NEU之间的关系可以根据欧拉定理通过两次转动来表示［12］。首先假设车辆停放在绝对水平面，此时的车辆坐标系XVYVZV与地理坐标系NEU完全重合，如图3所示。两次转动过程如图4所示。

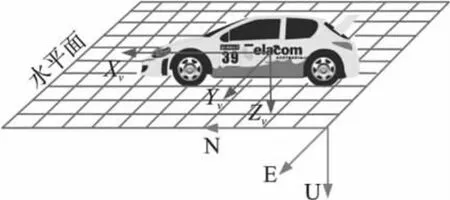
图3 坐标系重合

图4 转动过程

转动关系表示为:

其中α表示平面的倾斜角，β表示车辆前进方向与平面倾斜方向之间的夹角，两次转动变换矩阵为Cα，Cβ，任意向量在两个坐标系中的转换关系可以表示为:

化解上式可得:

联立式(2)和式(4)可以得到一个等式:

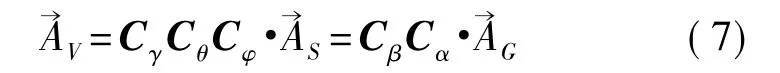
将式(3)和式(6)带入，式(7)写成矩阵形式为:

由于车辆停放的平面与水平面的夹角α固定不变，因此重力加速度g沿车辆坐标系ZV轴的分量gcosα是一个定值，不随车辆在平面停放角度β变化而变化，由式(8)可以得到一个等式:

由于ASX，ASY，ASZ是重力加速度在传感器各轴分量的测量值，可以通过多组测量值求解三角方程组得到α，γ，φ，θ值。但是由于测量误差的存在，直接求解可能无解或误差比较大。因此，需要通过数值分析的方法来进行求解。

2.2 安装误差的求解

式(9)可以看做是一个空间平面方程:

如果把加速度传感器三轴的输出看作是空间点的坐标(ASX，ASY，ASZ)，那么这些点就分布在这个空间平面上，在式(10)中:

如果可以确定空间平面方程(10)及停放平面与水平面的夹角α的值，就可以求解方程组(11)得到安装误差角度 φ，θ，γ［13］。

对空间平面方程(10)中A，B，C的确定可以用空间平面的最小二乘拟合方法，假设得到n组传感器测量数据(xi，yi，zi)，i=1，2…，n，则空间平面的最小二乘拟合方程如下:

通过方程(12)可以解得A，B，C的值［14］。α的值也可以通过解算加速度传感器测量数据来确定。上文提到传感器坐标系向车辆坐标系的转动关系，通过欧拉定理建立方程(3)。同理将车辆坐标系XVYVZV向传感器坐标系XSYSZS转动三次，每次转动角度λ，δ，ω可以得到方程:

式(13)与式(6)联立可以得到:

如果车辆在平面上两次停放角度β相差180°将两次传感器数据求和可以得到:

化简上式可以得到:

求解上式可以得到车辆停放平面与水平面夹角α。

将A，B，C和α的值代入式(11)，通过求解该方程组即可解得安装误差角φ，θ，γ，完成安装误差的标定。

3 标定方法的验证

为了验证标定方法的性能，通过模拟实验来进行测试。首先假设误差角度γ=5°，θ=6°，φ=7°，停放平面与水平面夹角α=5°。假设车辆在平面停放角度β分别为0°，30°，60°，…，330°，对应的模拟数据如表1所示，其中X，Y，Z表示传感器相应轴的数据，考虑到实际测量时加速度传感器静态随机误差(±0.001 gn)的存在，在数据中人为加入0.001 gn的随机噪声。

表1 模拟数据

图5

12组数据点(X，Y，Z)在三维空间内的分布如图5(a)所示，通过最小二乘法拟合出的空间平面在三维空间内的分布如图5(b)所示，拟合出的空间平面方程为:

将表1中β相差180°的数据代入式(16)，可以得到6个α的值。取α的均值α=5.1192°，α解算的相对误差为Er(α)=2.38%。

将式(17)的系数和α的值带入式(11)得到:

求解方程组 (18)，得到 γ =5.2999°，θ=6.1020°，φ=6.8984°。解算得到安装误差角平均相对误差为Er=2.84%，完全能够满足工程应用需求，证明标定方法是有效可行的。

4 结论

本文提出基于数学解算模型的三轴传感器安装误差的标定方法，不需要借助其他精密测量仪器，只需要安装传感器的车辆在任意平面停放数次，通过传感器的输出数据就可以完成安装误差的标定。通过模拟实验验证了该标定方法结算结果与预设值偏差小于3%，在可接受范围内，因此标定方法是有效的。在简易安装的情况下，经过标定后的三轴加速度传感器就可以实现对车辆行驶状态数据测量与采集。

［1］亓凤，顾青.MEMS传感器在汽车性能测试中的应用［J］.自动化仪表，2010，31(7):69－71.

［2］罗健飞，吴仲城，申飞.基于ARM的三维汽车振动加速度测量方法研究［J］.仪表技术与传感器，2010，4(4):87－88.

［3］杨华波，张士峰，蔡洪.无陀螺仪惯性系统构型中安装误差分析与标定［J］.中国惯性技术学报，2007，15(1):39－43.

［4］胡宇群，秦龙刚，黄翔.基于激光雷达的机载设备安装姿态校准［J］.南京航空航天大学学报，2010，42(1):112－116.

［5］马建萍.GPS辅助捷联惯导系统动基座初始对准新方法［J］.传感技术学报，2010，23(11):1656－1661.

［6］戴洪德，陈明，周绍磊，等.惯性导航系统非线性初始对准的LSSVM 方法研究［J］.传感技术学报，2007，20(7):1573－1576.

［7］MALEKI A F.Two-Point Calibration of a Longitudinal Acceleration Sensor［P］.US，6347541B1.2002－2－19.

［8］TAKAHASHI M，KONDO Y.Three-Axis Acceleration Sensor Variable in Capacitance under Application of Acceleration［P］.US，5383364.1995－1－24.

［9］张金.基于ARM的车辆姿态测量系统设计［D］:［硕士学位论文］.北京:北京交通大学电子信息工程学院，2008.

［10］杨杰，史震，岳鹏，等.三轴加速度计GFSINS安装误差标定与补偿方法［J］.系统工程与电子技术，2011，33(4):869－878.

［11］KROHN A，BEIGL M，DECKER C，et al.Inexpensive and Automatic Calibration for Acceleration Sensors［J］.Ubiquitous Computing Systems，2005:245－258.

［12］李怡凡，吴黎明，张力锴.一种车身姿态的捷联测量［J］.传感技术学报，2010，23(8):1189－1194.

［13］覃方君，许江宁，傅军，等.一种简化的无陀螺惯导系统安装误差校准方法［J］.测试技术学报，2008，22(2):155－159.

［14］崔敏，马铁华，张慧，等.基于十二加速度计的GFSINS安装误差标定及补偿［J］.中国惯性技术学报，2009，17(4):413－418.