股指收益率与成交额间引导关系分析
吴明华,周爱民,宋敏
(南开大学经济学院,天津300071)
股指收益率与成交额间引导关系分析
吴明华,周爱民,宋敏
(南开大学经济学院,天津300071)
文章运用风险研究领域中应用广泛的Copula分析法,考察我国上证指数及深成指日收益率与成交额之间的相互引导关系。结论显示,成交额变动率与滞后其一个交易日的股指收益率之间不存在引导关系;股指收益率对滞后其一个交易日的成交额变动率存在先导作用,不过这种先导作用对滞后其两个交易日的成交额变动率不存在。此外,股指收益率与滞后其一个交易日的成交额变动率间的关联模式表现为尾相关。
收益率;成交额;Copula模型
0 引言
交易量与股价(股指)作为市场行为信息指标,由于直接反应股票(股市)的交投情况而备受市场关注,量价之间的关系也一直是技术分析领域中的研究热点。华尔街有两句谚语:“牛市成交量大,熊市成交量小”及“量推价走”,更通俗的说法即是:“价涨量增、价跌量减”,“量在价先行”。
成交量与价格之间到底是否存在着相互引导关系?许多学者曾对这个问题进行过研究。Hiemstra and Jones(1994)[1]研究了道琼斯综合指数日收益率与成交量间的引导关系,结论显示二者存在着显著的双向非线性因果关系。Silvapulle and Choi(1999)[2]采用Granger因果检验法对韩国股票市场指数日收益率与成交量间关系进行研究,结果显示二者具有双向线性和非线性因果关系。我国学者对交易量与收益变动的引导关系也进行了大量的研究,不过结论差异较大。魏巍贤,康朝锋(2001)[3]利用上证综合指数日收益率与成交量数据,研究发现价格和成交量对预测对方有显著作用。芮萌、孙彦丛与王清和(2003)[4]对沪深A、B股日交易数据进行研究,结论显示任何一个市场上交易量均不Granger引导市场收益。张博(2008)[5]以上海A股综合指数日收益率及日交易金额数据为分析对象,研究结论认为交易量中的信息交易量对于价格变动具有较高的解释能力,且该市场存在价量之间双向Granger因果关系。董秀良,吴仁水(2008)[6]利用中国沪深股市日交易数据,采用多元GARCH模型进行实证研究,结论显示沪市股指收益与成交量间具有双向引导关系,而在深市只存在收益对成交量变化的单向引导关系,不过文章作者指出,沪市指数编制存在问题,因此判定收益对成交量变化具有单向先导作用。
从股指走势图中观察,量价间引导关系具有不确定性。通常,价格及交易量小幅波动时,二者间关联关系很难捕捉,而波动较大的量、价在实践中受到重点关注。本文借鉴在风险研究领域中应用广泛的Copula分析法,并首次将其引入量价关系的研究中。采用Copula分析法一方面可以找到量与价的联合分布,另一方面可以发现量价变化较明显时二者间的关联关系。
1 Copula分析法
1.1 本文所涉及的二元Copula函数简介[10]
1.1.1 Gumbel Copula函数
Gumbel Copula函数的分布函数和密度函数分别为:
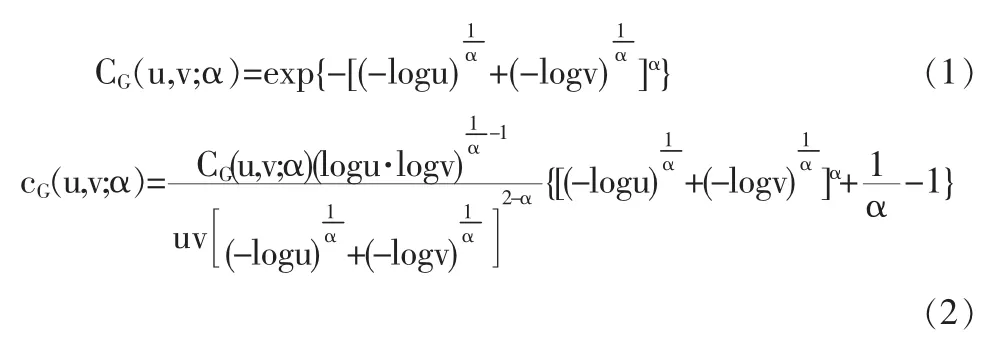
其中α(α∈(0,1])为相关参数。当α=1时,CG(u,v;α)=u· v,随机变量u、v相互独立;当α→0时,随机变量u、v趋向于完全正相关。
1.1.2 Clayton Copula函数Clayton Copula函数的分布函数和密度函数分别为:

1.1.3 Frank Copula函数Frank Copula函数的分布函数和密度函数分别为:

此外,用线性组合的方法,可以根据已有Copula函数构造更多的Copula函数(参考Nelsen(1998)[8]),如由以上三个二元Copula函数可以构造混合Copula函数:

其中wG、wC、wF为权重,满足wG+wC+wF=1,且0≤wG,wC,wF≤1。
1.2 Copula函数的参数估计
Copula函数的参数估计方法有很多(参见罗俊鹏(2005)[9]),其中伪极大似然估计法较为常用,该方法不需指定边缘分布,从而可避免由错选边缘分布所导致的参数估计错误。伪极大似然估计法分为两个步骤,下面以二元混合Copula函数的参数估计为例进行介绍。
首先,用经验分布对边缘分布建模如下:
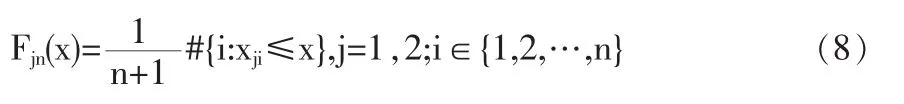
其中n为观测值组数。这样,每组观测值Xi=(x1i,x2i),i= 1,2,…,n,经式(11)变换后,得到相应拟观测值:(ui,vi)=(F1n(x1i),F2n(x2i)),i=1,2,…,n。
然后,基于已得拟观测值,构造伪似然函数:

其中c(·)表示式(10)中混合Copula函数的密度函数,β=(α,θ,λ,wG,wC,wF)为待估参数。使式(12)中似然函数值极大化的估计值β赞,即为上述二元混合Copula函数的伪极大似然估计量。
1.3 拟合优度检验
根据已得伪极大似然估计量,可以确定二元Copula函数的具体形式,从而找出变量间的相关关系。然而所确定的Copula函数是否合适,还需进行拟合优度检验。由于我们采用伪极大似然法估计参数,相应可以选取边缘分布未知时的χ2拟合优度检验。
设Apq,p=1,2,…,r;q=1,2,…,s是对区域[0,1]×[0,1]的一个划分,相应地,令:


在所估计Copula函数合适的零假设之下,下列统计量M服从自由度为(r-1)(s-1)-m的χ2分布:

其中m为所估计Copula模型中包含参数的个数。
2 实证研究
2.1 数据来源与选取
本文选取我国上证指数,深圳成份指数的收盘值及成交金额序列为研究对象。之所以选取交易金额为反应交易量的指标,是因为各股票价格不一,且通常投资者以投入资金的多少来表征其对某只股票及市场前景的看好程度,因此认为交易金额比以股数为单位的交易量更能反应市场的交投状况。各时间序列范围为1999年8月2日至2010年2月9日,序列长度为2545。1999年7月,我国第一部《证券法》实施,尽管之后曾多次对其做出修订,但该法案的实施,在一定程度上规范了市场交易行为。随着监管的发展及市场的扩容,市场指数越来越不易被操纵,其价格与成交额能较真实地反应市场状况及交易者行为。
数据来源于大智慧行情分析系统。所应用的数据分析软件是MATLAB 7.1。
2.2 实证分析
由于股指收盘值与成交金额序列均为具有自相关性、异方差性的单位根过程,因此在进行Copula分析之前,需要将各序列处理为独立同分布观测值。首先为各序列取对数后做一阶差分,分别以Rsh、Rsz与Ash、Asz表示对数上证指数、深圳成指收盘点数及成交金额序列差分后的值,即为沪、深股指收益率与成交额变动率序列。然后对各序列进行GARCH变换以去掉其自相关性及异方差性,结果见表1。

表1 各序列去自相关性及异方差性变换
变换后的各标准化残差序列有效长度不同,为此我们取其第11-2545的子序列进行研究,各序列名称不变,长度均为2535。此外,下文中的收益率及成交额变动率均指经GARCH变换后相应标准化残差序列。
根据式(11),可得(ush,vsh)及(usz,vsz)的拟观察值序列分别为:(Ush,Vsh)与(Usz,Vsz)。
2.2.1 收益率对成交额变动率的引导关系检验
为检验沪、深股市收益率对成交额变动率的引导关系,我们分别取Ush、Usz的前2534个值作为新序列Ushb、Uszb;取Vsh、Vsz的后2534个值作为新序列Vsha、Vsza,并组成两对:(Vshb,Vsha)及(Uszb,Usza),采用Copula分析法分别进行研究。
应用伪极大似然法估计Copula参数,经计算,混合Copula模型的极大似然值最大,并计算相应拟合优度检验统计值M,结果见表2。

表2 Copula模型拟合结果
对上证指数考察时,由于第一组估计结果显示混合Copula中Gumbel分布的权重值不显著,将其去掉后重新进行估计,因而呈现了两组估计结果。表2中的M值由式(15)求得,这里我们将区域[0,1]×[0,1]划分为15×15个单元格。临界值依次是自由度为190、192、190的χ2分布上侧5%分位数。
由表2中M值均小于其临界值可知,上证指数收益率与滞后一个交易日的成交额变动率即(Ushb,Vsha)的联合分布,可由权重分别为0.4969与0.5031的Clayton Copula和Frank Copula组成的混合Copula函数表出;深成指收益率与滞后一个交易日的成交额变动率间即(Uszb,Vsza)的联合分布,可由Gumbel Copula、Clayton Copula和Frank Copula三者组成的混合Copula函数表出,权重分别为0.4507、0.3063及0.2430。
两组变量的经验频率分布及所估计模型频率分布分别见图1、图2与图3、图4。



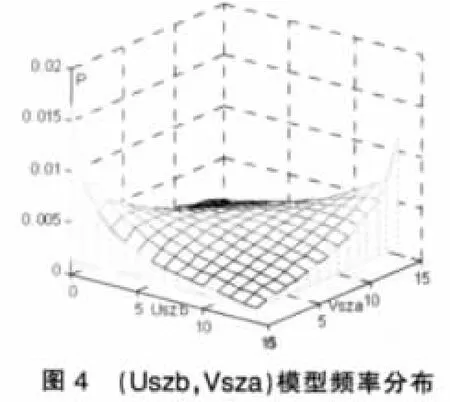
综上,沪、深股市收益率与滞后一个交易日的成交额变动率间的联合分布,可由混合Copula函数表出,因此可以判定沪、深股市收益率对成交额变动率具有先导作用。此外,收益率与滞后一个交易日的成交额变动率间的相关模式为尾相关:由图1、图2及图3、图4可以看出,联合频率在二者同时取较大值或较小值时,即其上、下尾部,较高,且下尾部的频率稍高于上尾部的;二者之一取较大值而另一取值较小时很低。这意味着,股指涨幅较高时,下一交易日的成交额将相对扩大的可能性很高;股指跌幅较大时,下一交易日的成交额将相对萎缩的可能性非常高,且股指下跌后成交额萎缩的可能性稍高于指数上涨后成交额扩大的可能性。
根据以上分析,股指上涨后,股民热情参与,“追涨”行为表现比较突出;股指下跌后,股民表现谨慎,进一步“杀跌”行为不明显。这与一般认为我国股民惯于“追涨杀跌”不完全相同,但与“牛市成交量大,熊市成交量小”这句谚语相吻合。
2.2.2 成交额变动率对收益率的引导关系检验
为检验沪、深股市成交额变动率对收益率的引导关系,我们分别取Vsh、Vsz的前2534个值作为新序列Vshb、Vszb;取Ush、Usz的后2534个值作为新序列Usha、Usza,并组成两对:(Usha,Vshb)及(Usza,Vszb),采用Copula分析法分别进行研究。
应用伪极大似然法估计Copula参数,经计算发现所有参数都不具有显著性,结果在此不赘述。另外,观察(Usha,Vshb)及(Usza,Uszb)的经验频率分布图,见图5、图6,发现两组变量均有可能相互独立,为此验证其独立性如下。
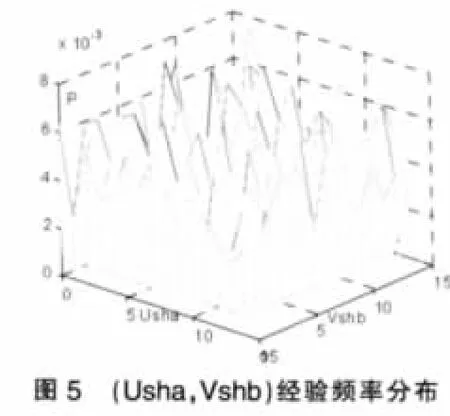

我们依然采用χ2拟合优度检验法,将区域[0,1]×[0,1]划分为15×15个单元格。此时,令,p=1,2,,…,15;q=1,2,…,15。经计算变量(Usha,Vshb)及(Usza,Vszb)的M值分别为:221.6012、190.8864,二者皆小于自由度为196的χ2分布的上侧5%分位数229.6632。因此可以判定Usha与Vshb及Usza与Vszb均相互独立,即沪、深股市成交额变动率对下一交易日的收益率不存在引导关系。
2.2.3 收益率对滞后其两个交易日成交额变动率的引导关系检验
由前面结论知,沪、深股市收益率对滞后一个交易日的成交额变动率具有先导作用,那么其对滞后两个交易日的成交额变动率是否也有先导作用呢?下面对此进行检验。
分别取Ush、Vszaa的前2533个值作为新序列Ushbb、Uszbb;取Vsh、Vsz的后2533个值作为新序列Vshaa、Vszaa,并组成两对:(Ushbb,Uszbb)及(Uszbb,Uszaa)。
观察(Ushbb,Vshaa)及(Uszbb,Vszaa)的经验频率分布图,即图7与图8,发现两组变量均可能相互独立,下面验证其独立性。


仍然采用前面验证独立性时的χ2拟合优度检验法。经计算,变量(Ushbb,Vshaa)及(Uszbb,Vszaa)的M值分别为:225.8956及180.1078,二者均小于临界值229.6632。由此可知,沪、深股市收益率对滞后两个交易日的成交额变动率不具有先导作用。
3 结论
本文基于沪、深股市日交易数据,借鉴在风险研究领域中应用广泛的Copula分析法,研究了收益率与成交额变动率间的相互引导关系。结论显示,成交额变动率与滞后其一个交易日的股指收益率间不存在引导关系;股指收益率对滞后其一个交易日的成交额变动率存在先导作用,不过这种先导作用对滞后其两个交易日的成交额变动率不存在。
此外,股指收益率与滞后其一个交易日的成交额变动率间的相关模式表现为尾相关:其联合频率在二者同时取较大值或较小值时,即其上、下尾部,较高,且下尾部的频率稍高于上尾部的;在二者之一取较大值而另一取值较小时很低。这意味着,股指涨幅较高时,下一交易日的成交额将相对扩大的可能性很高;股指跌幅较大时,下一交易日的成交额将相对萎缩的可能性非常高,且股指下跌后成交额萎缩的可能性稍高于指数上涨后成交额扩大的可能性。据此可知,股指上涨后,股民热情参与,“追涨”行为表现比较突出;股指下跌后,股民表现谨慎,进一步“杀跌”的行为不明显。这与“牛市成交量大,熊市成交量小”这句谚语相吻合,但与一般认为的我国股民惯于“追涨杀跌”不完全相同,我们认为我国股民惯于“追涨”,但“杀跌”只在股价上升一段后的反转之初,即获利盘较多时,有所表现;在股价已有一定跌幅,被套牢时,股民则倾向于捂盘待涨。
本文结论及芮萌,孙彦丛,王清和(2003)[4]、董秀良,吴仁水(2008)[6]基本结论均认为成交额或成交量对股指收益率没有引导作用,与“量在价先行”相矛盾,这是否是中国股市所独有的特性,有待于进一步基于个股及不同周期的数据进行验证。
[1]HiemstraC,JonesJD.TestingforLinearandNon-linear Granger Causality in the Stock Price-volume Relation[J].Journal of Finance,1994,54(5).
[2]Silvapulle P,Choi J S.Testing for Linear and Non-linear Granger Causality in the Stock Price-volume Relation:Korean Evidence [J].The Quarterly Review of Economic and Finance,1999,39(1).
[3]魏巍贤,康朝锋.上海股市价量关系的实证分析[J].预测,2001,(8).
[4]芮萌,孙彦丛,王清和.中国股票市场交易量是否包含预测股票收益的信息研究[J].统计研究,2003,(3).
[5]张博.上海证券A股市场价量关系实证研究[J].财经问题研究,2008,(2).
[6]董秀良,吴仁水.交易量适合作为股价波动信息的代理变量吗?[J].数量经济技术经济研究,2008,(1).
[7]Sklar A.Fonctions de Repartitionàn Dimensions et leurs Marges [J].Publication de l'Institut de Statistique de l'Universitéde Paris, 1959,(8).
[8]Nelsen R B.An Introduction to Copulas[M].New York:Springer, 1998.
[9]罗俊鹏.Copula理论及其在金融分析中的应用研究[D].天津:天津大学理学院,2005.
[10]韦艳华.Copula理论及其在多变量金融时间序列分析上的应用研究[D].天津:天津大学管理学院,2004.
(责任编辑/浩天)
F830.9
A
1002-6487(2011)05-0141-04
南开大学基本科研业务专项资金项目(NKZXB10052)
吴明华(1982-),女,博士研究生,研究方向:资本市场及金融工程。
周爱民(1961-),男,教授,博士生导师,研究方向:资本市场及金融工程。

