基于生产函数的行业规模效益实证分析

刘小军，刘澄，鲍新中

(北京科技大学经济管理学院，北京100083)

基于生产函数的行业规模效益实证分析

刘小军，刘澄，鲍新中

(北京科技大学经济管理学院，北京100083)

做大作强是当前我国企业适应国际市场竞争的一种战略选择，为了使企业更加明确自身从质和量两个方面发展的要求，对行业规模效益进行分析就显得非常重要。文章基于C-D生产函数和CES生产函数构建了不同的行业规模效益检验模型，并对上市公司按行业分类的样本数据进行回归分析，最后对两个生产函数得到的行业规模效益结论进行比照分析，得到各行业规模效益的相关结论。

生产函数;规模效益;参数估计;要素投入;效率系数

0 引言

20世纪60年代以来，企业得到快速扩张，平均资产规模增大的同时，大企业的数量也迅猛增加。企业的做大做强是一种战略选择。大企业的发展包含了不同层面的内容，是质与量的统一：一是资产规模的扩大；二是企业竞争能力的扩张；三是企业内部经营管理和企业组织形式的发展变化。这几个方面是在企业成长过程中逐步积累的，单纯从某一方面所表现出的企业扩张是不能持久的，只有相互间互为依托，互相促进，才能称为成功的企业扩张。从这个角度说，对行业和企业的规模效益进行研究就显得非常必要。

目前对行业或者企业规模效益的研究方法主要有两类:一类文献是利用数据包络分析方法来分析各个企业的规模有效性[1-5]；第二类文献利用采用生产函数法来测度企业的规模经济性[6-11],一般是按照科布-道格拉斯（C-D）生产函数假设的投入和产出变量之间的显性指数关系展开实证研究。由于C-D生产函数的替代弹性恒为1，而生产函数的应用之一就是研究要素之间替代的可能性，在不同的企业、行业之间这种替代的可能性可以是相当不同的，而C-D生产函数不能反映这种差异。而常替代弹性生产函数（CES）就是针对这一限制提出的。本文将分别采用C-D生产函数和CES生产函数构建不同的行业规模效益检验模型，并分别对上市公司按行业分类的样本数据进行回归分析，最后对两个生产函数得到的行业规模效益结论进行比照分析。

1 基于生产函数的行业规模效益模型构建

1.1 利用C-D生产函数构建企业规模效益模型

1928年由美国科学家Charles Cobb和经济学家Paul Dauglas提出的生产函数在实际中得到了最广泛的应用。在两投入要素下，其形式为:

其中K、L为要素投入量，A为效率系数，α和β为K和L的产出弹性，A、α、β均为待估参数。C-D函数有如下特点：

（1）参数α、β分别是产出的劳动弹性与资金弹性。

（2）产出的弹性之和是函数齐次性的阶α+β，从而当

利用C-D生产函数的α+β与生产函数规模报酬的特性，可推导出行业的规模效益，但是由于原C-D函数为指数形式而非线性形式，因此难以利用历史上的产出Q、资本K、劳动力L的值估计出此形式的α和β的值，为了能够估计出α和β的值，可构造如下的C-D对数生产函数，将C-D函数转化为线性函数:

此生产函数为线性函数，因此可用历史数据利用最小二乘估计估计出行业的α和β的值。

1.2 利用CES生产函数构建企业规模效益模型

1961年由Arrow、Chenery、Mihas和Solow四位学者提出了两要素CES生产函数，其基本形式为：

其中，A为效益系数，δ为分配系数，ρ为替代系数，0< δ≤1，-1≤ρ<∞。它区别于C-D生产函数的主要点在于要素替代弹性不是1。当ρ=0时，σ=1，式（3）与C-D函数是一致的。式（3）是不变规模报酬时的情形，更一般的形式是

其中，μ是反映规模报酬的参数，当

由于CES生产函数不能简单地变为线性形式，其估计方法也较复杂。自1961年以来，关于其估计问题有许多研究，这里应用直接估计方法。直接估计方法，是通过台劳级数展开式将式（4）展开，取前面几项，得到线性计量经济学方程，这是有Kementa于1967年提出的。对式（4）取对数，得

并在ρ=0处作台劳展开，取关于ρ的线性部分

式（6）的前三项相当于ρ=0时的CES生产函数，显然，它就是C-D生产函数的形式；后一项是对ρ=0的结果的一个调整，取决于ρ的大小。可见，式（6）近似式（4）的误差大小取决于ρ偏离0的程度。若估计出的ρ接近于0，则参数估计量是较好的近似，若ρ值与0相差较大，则参数估计量不是较好的近似。

2 上市公司分行业规模效益的实证研究

2.1 样本和数据

为了衡量各行业的规模经济效应现状，利用CCER数据库中2008年上市公司的财务数据，作为原始数据对各行业的系数值进行估计，各变量的数据采集方法如下：（1）Q取值为营业收入(单位:元)；（2）K取值为总资产(单位:元)；（3）L取值为职工人数(单位:人)。

根据摩根斯坦利和标准普尔公司联合发布的全球行业分类标准(GICS)，考虑到每个行业需要足够数量的上市公司，这里一共选取了20个行业（所选行业中各行业上市公司样本较多）1083家上市公司，各样本的Q、K和L的具体取值就不一一列示，仅列出各个行业的公司样本数。如表1所示。

表1 样本数按行业分类表

2.2 C-D模型参数估计值

以式（5）为原型建立回归模型，按行业分类对样本数据进行回归分析（使用统计软件SPSS 13.0），各行业的α、β的估计值以及拟合优度R2如表2所示。

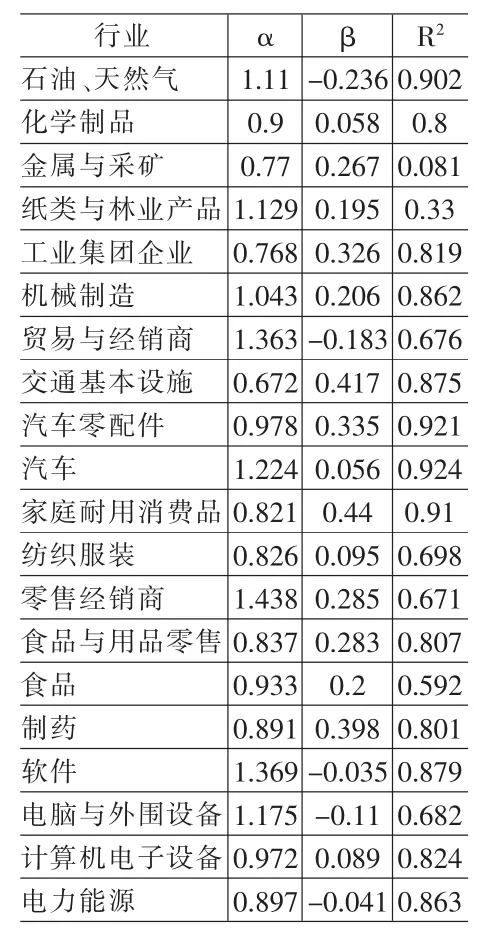
表2 上市公司按行业分类的资金弹性、劳动弹性及拟合优度表

其中:

α、β:为资本、劳动力对总产出的弹性，它表示资本、劳动力的变化量带来的总产出的变化量。

R2：为拟合优度，又称可决系数：

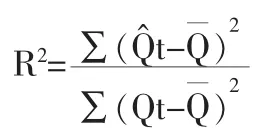
R2值介于0与1之间，它表示总产出的变化有多大的因素是由资本和劳动力决定的，R2值越接近1表明拟合的效果越好，通常要求R2大于或等于0.8。

由表2中的α、β、R2的数据分析可得:

（1）α、β是总产出工业总产值的资本弹性和劳动力弹性，即资本和劳动力扩大倍时总产出将扩大λα+β倍。考虑行业规模扩大λ>1情况，有:

如：机械制造行业的α=1.043、β=0.206，假设机械制造行业生产规模扩大了一倍，营业收入将扩大21.249/2=1.188倍，即效益递增。

（2）R2值表示的是拟合的程度。如:机械制造行业的R2= 0.862，表示机械制造行业产出的增减有86.2%是由资本和劳动力决定的。

2.3 CES模型参数估计值

首先将原数据进行求对数等处理，得到相应的因变量lnQ以及对应的自变量即得到进行回归分析所需的样本数据。以式（6）为原型建立回归模型，按行业分类对样本数据进行回归分析（使用统计软件SPSS 13.0），得到系数μρ、μ(1-δ)和的值，进而得到各行业的μ值，根据μ值可以判断各行业是规模效益递增还是递减，或者是不变。回归分析所得到的各行业μ值及拟合优度R2的值如表3所示。

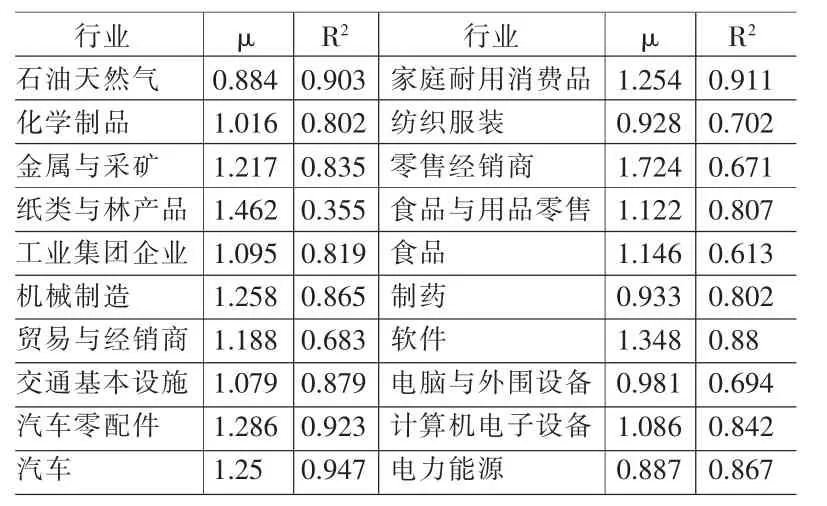
表3 各行业上市公司参数值及拟合优度

由表3中的μ和R2的数据分析可得:

（1）μ是反映规模报酬的参数，即资本和劳动力扩大λ倍时总产出将扩大λμ倍。考虑行业规模扩大λ>1情况，有:

如:汽车零配件行业的μ=1.286，假设汽车零配件行业生产规模扩大了一倍，其营业收入将扩大21.286/2=1.219倍，即效益递增。

（2）R2值表示的是拟合的程度。如:汽车零配件行业的R2=0.923，表示汽车零配件行业产出的增减有92.3%是由资本和劳动力决定的。

3 上市公司规模效益的实证结果分析

3.1 C-D模型研究结果

由C-D函数的分析可以得到如下结论：

（1）多数行业存在着规模效益递增效应（16个）。规模效益递增的行业见表4所示。

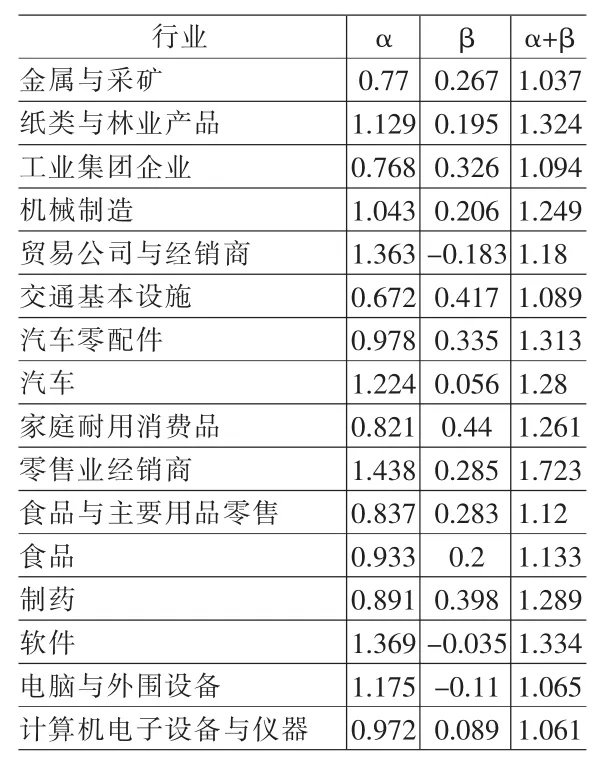
表4 上市公司规模效益递增的行业

（2）部分行业存在规模效益递减效应（4个）。规模效益递减的行业见表5所示。

表5 上市公司规模效益递增的行业

3.2 CES模型研究结果

由CES生产函数的分析可以得到如下结论：

（1）多数行业存在着规模效益递增效应（15个）。规模效益递增的行业见表6所示。

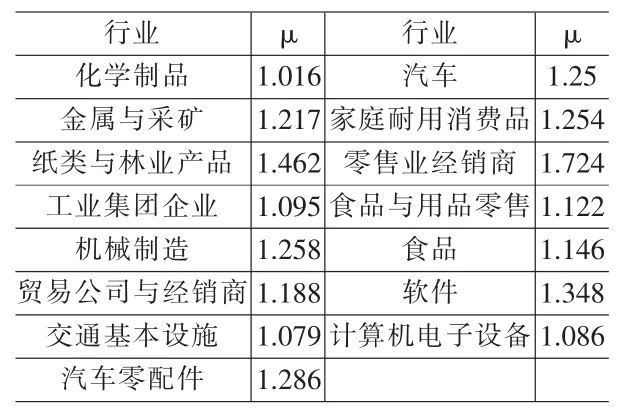
表6 上市公司规模效益递增的行业

（2）部分行业存在规模效益递减效应（5个）。规模效益递减的行业见表7所示。

表7 上市公司规模效率递增的行业

3.3 两种模型研究结果的比较

这里我们分别分析了两组模型的的回归结果，不难发现依据C-D函数和CES函数构建的两个模型进行回归分析所得出的结论基本一致。为获得更加直观的比较效果，将两种模型分别得出的各行业规模效益情况列于表8。

表8 两种模型的回归分析结果

从表8中可以看出，除了化学制品行业、制药和电脑与外围设备行业之外，依据两组系数估计值所推得的其他行业的规模效益情况完全一致。

4 结论

分别运用C-D生产函数和CES生产函数构建了行业规模效益的检验模型。运用2008年度我国20个行业共计1083家上市公司财务及相关数据，对两个模型分别进行了回归分析，结果表明，两个生产函数得到的行业规模效益结论是基本一致的。

在20个行业中，金属与采矿、纸类与林业产品、工业集团企业、机械制造、交通基本设施、贸易公司与经销商、汽车零配件、汽车、家庭耐用消费品、零售业经销商、食品与主要用品零售、食品、软件、计算机电子设备与仪器共14个行业，利用两个生产函数得到结论一致，这15个行业存在不同程度的规模效益递增效应；而石油天然气与消费用燃料、纺织品服装与奢侈品、电力能源3个行业存在着规模效益递减的趋势；化学制品、制药行业和电脑与外围设备3个行业通过两个生产函数得到的分析结果不一致，规模效益趋势不明朗。

[1]郝清民,张兆江.钢铁企业规模经济有效性研究[J].钢铁研究,2003,132(3).

[2]Shaffer S.Firm Size and Economic Growth[J].Economic Letters, 2002,(76).

[3]Jeffrey T.M.Technological Development and the Boundaries of theFirm:AKnowledge-basedExaminationinSemiconductor Manufacturing[C].Working Paper.Robert E.McDonough School of Business Georgetown University,2006.

[4]徐旭川,杨丽琳.公共投资就业效应的一个解释[J].数量经济技术经济研究,2006，(11).

[5]熊林峰,林君芬,黄一鸣.中国注册会计师行业规模报酬与规模经济效应研究[J].财会通讯,2006，(6).

[6]云鹤,吴江平.“浙江模式”的C-D形式检验及启示——基于CES生产函数[J].浙江理工大学学报,2009，(3).

[7]王贻志,孙阳,阮大成.应用二级CES生产函数对中国制造业R&D投入产出效应的实证研究[J].数量经济技术经济研究,2006，(8).

[8]Staffan C.Bureaucratic Limits of Firm Size:Academic Summary [C].Working Paper,2003,(4).

[9]张小蒂,李晓钟.对我国长三角地区全要素生产率的估算与分析[J].管理世界,2005，(11).

[10]左小德,林文兴,梁云.广东企业规模效益的实证研究[J].数学的实践与认识,2008,38(18).

[11]黄大全,滕艳丽,张华,梁进社.基于生产函数的城市经济水平影响因素差异研究[J].城市经济,2009,(3).

（责任编辑/浩天）

F062.1

A

1002－6487（2011）05-0099-03

刘小军（1974-），男，陕西宝鸡人，博士研究生，研究方向：产业经济，经济个体行为。

刘澄（1967-），男，辽宁辽阳人，教授，博士生导师，研究方向：金融工程。

鲍新中（1968-），男，江苏宜兴人，博士，副教授，研究方向：财务管理。