动态因子模型与ARMA模型的比较

杜勇宏，王健，王汝芳

（1.南开大学经济学院，天津300071；2.北京物资学院经济学院，北京101149）

动态因子模型与ARMA模型的比较

杜勇宏1，王健1，王汝芳2

（1.南开大学经济学院，天津300071；2.北京物资学院经济学院，北京101149）

在时间序列模型中，随着变量数目的增加，所要估计的参数的数量也随之加大，结果在应用中模型中通常不得不选取尽量少的变量。动态因子模型独特的优势在于，它不必考虑自由度损失问题，也不必对经济结构施加约束。文章根据中国宏观经济变量数据库中的41个变量，建立了动态因子模型预测GDP，并与ARMA模型的预测结果进行了对比。结果显示，动态因子模型的预测效果优于ARMA模型。

动态因子；ARMA模型；预测

0 引言

在时间序列模型中，随着变量数目的增加所要估计的参数的数量也迅速加大，使得应用中不得不选用尽量少的变量建立模型。在实际应用中，迫切需要对大量的经济和金融时间序列组成的数据集进行分析，动态因子模型领域的研究应运而生。Sargent和Sims(1977)对Burns和Mitchell(1946)提出的静态因子模型进行了改进，提出动态因子模型。Geweke（1977）采用动态因素模型提取合成指数研究了经济周期。近年来，多维动态因子模型得到了广泛的发展与应用。

在应用计量经济学中，如何对GDP和通货膨胀进行更好的预测始终是研究的焦点。最近的文献中，Stock和Watson (1999)采用单变量模型预测了美国的GDP，Stock和Watson(2001)采用因子模型预测了美国的GDP。Camba-Mendez,Kapetanios,Smith和Weale(2001)利用多个先行指标组成的系统预测总产出。

本文主要关注动态因子模型和单变量ARIMA模型哪个更适用于预测GDP？对预测精度的改进程度有多大？本文拟采用动态因子模型，借助STATA软件，对中国GDP进行预测，建立分析框架。

1 动态因子模型及其估计和预测

目前，动态因子模型广泛应用于预测美国、英国和欧洲的宏观经济变量(Stock and Watson(2001),Artis,Banerjee和Marcellino(2005)，Marcellino,Stock和Watson(2002))。我们不是根据某个变量或者某几个变量提取信息，而是从大量数据序列中提取最重要的因子并利用这些因子进行预测。下面，我们首先简介动态因子模型。令

yt=Pft+Qxt+ut

ft=Rwt+A1ft-1+A2ft-2+…+Apft-p+vt

ut=Cut+C1ut-1+C2ut-2+…+Cput-p+et

其中，yt是内生变量组成的k维向量，ft是不可观测的因子组成的n维向量,xt是外生变量组成的矩阵，扰动vt、et独立同分布。在动态因子模型中，内生变量组成的向量受到一些不可观测的因子以及外生变量的影响。不可观测的因子及扰动具有向量自回归的结构。

STATA 11.0中，采用极大似然估计（MLE）对模型进行参数估计。模型被写成状态空间的形式的，使用卡尔曼滤波的方法计算似然函数。动态因子模型非常宽泛，需要对参数施加必要的限制才能识别。STATA 11.0中命令dfactor默认参数是可识别的，因子的识别与符号无关，即不可观测的因子的系数估计改变符号并不改变预测和似然函数的值。

2 模型的估计和预测

下面，采用动态因子模型预测中国的GDP。本文选取41个宏观经济变量构成研究对象，数据包括1993年第一季度到2009年第三季度共67个季度。所有数据来自历年《中国统计年鉴》、CCER金融经济数据库。对变量序列首先进行了预处理，包括：（1）采用X-12方法对序列进行季节调整性；（2）对调整后的变量的非平稳性进行单位根检验，检验中充分考虑到中国在经济转型阶段所表现出的非线性特征。检验结果①表明，序列是存在多个结构突变点的趋势平稳过程；（3）对季节调整后序列采用广义普通最小二乘GLS方法退除趋势。

因子模型可以含有较多的变量，但是并不是变量越多越好[Boivin和Ng（2003），Watson（2000）]。因此，需要对变量进行筛选，本文中对预处理后的数据计算各个变量与GDP的交叉相关系数，结果见表1。其中，先行期数最长为5期，最后一列为算术平均。按照与GDP的相关程度强弱，表中第一列是对变量进行了排序的结果。

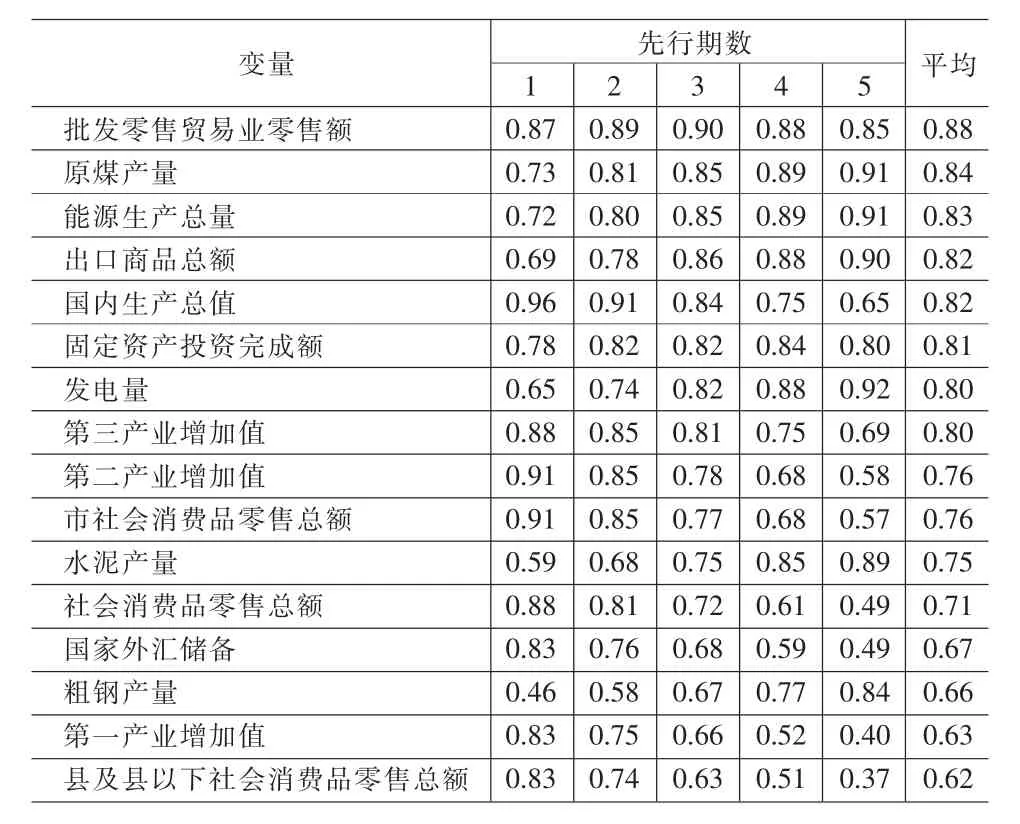
表1 各个变量与GDP的交叉相关系数

采用软件STATA 11.0估计动态因子模型。LR检验显示，模型仅需选择一个共同因子，估计结果见附录。下面，对因子模型与ARMA模型的预测结果进行对比分析，结果见表2和表3。其中预测精度用RMSE和MAE予以度量。在ARMA模型中，AR和MA项数也基于RMSE最小化原则予以确定。由表2可知，因子模型样本内的预测效果明显好于ARMA模型。此时，因子模型的RMSE比ARMA模型的RMSE低46%；因子模型的MAE比ARMA模型的MAE低53%。由表3可知，样本外因子模型的预测效果也明显好于ARMA模型。

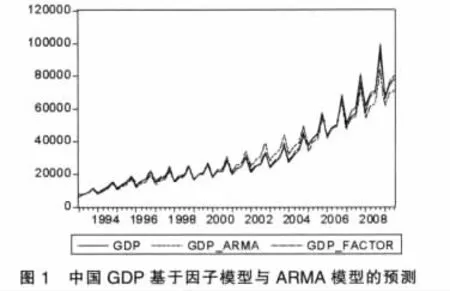
图1是中国GDP序列基于因子模型与ARMA模型的预测结果，显然，因子模型比ARMA模型的预测结果更为理想。

表2 因子模型与ARMA模型的预测结果(样本内)

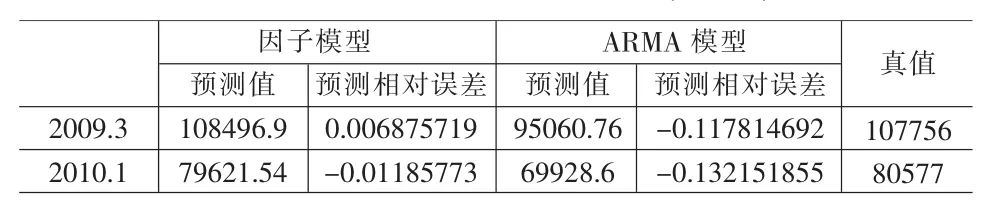
表3 因子模型与ARMA模型的预测结果(样本外)

3 结论

动态因子模型充分利用宏观经济变量之间的关联和共性特征，合成少量的指标来描述影响这些变量波动的共同因素，并对因子的动态性予以刻画。与单变量ARMA模型相比，多维动态因子模型有其独特的优势。首先，因子模型可以处理大量的变量，而不必考虑回归分析中需要面临的自由度损失问题。从而使得研究人员和决策者在研究中能够采用比以往更详尽的数据，进行更精确的预报和宏观经济分析。其次，动态因子模型可以将个性因素（包括测量误差和局部冲击）分离出来。这将向决策者提供更加可靠的信息，并且防止他们受到个性因素的影响。另外，动态因子模型不必像结构模型那样对变量间的结构关系进行严格的假设，条件非常宽泛。

本文根据中国宏观经济变量数据库中的41个变量，建立动态因子模型预测GDP，并与ARMA模型的预测结果进行对比。结果显示，不管是在样本内的拟合还是样本外的动态预测，动态因子模型的预测效果都明显优于ARMA模型。

[1]Artis,M.,Banerjee,A.,Marcellino,M.Factor Forecasts for the UK[J].Journal of Forecasting,2005,（24）.

[2]Burns A,Mitchell W.Measuring Business Cycles[M].New York: National Bureau of Economic Research,1946.

[3]Geweke,J.The Dynamic Factor Analysis of Economic Time Series Models.In Latent Variables in Socioeconomic Models[M].Amsterdam:North-Holland,1977.

[4]Marcellino,M.,Stock,J.H.,M.W.Watson.Macroeconomic Forecasting in the Euro Area:Country Specific Versus Euro Wide Information[J].European Economic Review,2003，(47).

[5]Sargent T.J.,C.A.Sims.Business Cycle Modeling without Pretending to Have too Much a Priori Economic Theory.In New Methods in Business Cycle Research:Proceedings from a Conference, ed.C.A[M].Sims,Minneapolis:Federal Reserve Bank of Minneapolis, 1977.

[6]Stock J.H.,M.W.Watson.New Indexes of Coincident and Leading Economic Indicators[M].Cambridge,MA:MITPress,1989.

[7]Stock,J.H.,M.W.Watson.A Comparison of Linear and Non-linear Univariate Models for Forecasting Macroeconomic Time Series [M].Oxford:Oxford University Press,1999.

[8]Stock,J.H.,M.W.Watson.Forecasting Output and Inflation:The Role of Asset Prices[C].NBER Working Paper,2001.

[9]Stock,J.H.,M.W.Watson.Macroeconomic Forecasting Using Diffusion Indexes[J].Journal of Business and Economic Statistics,2002, (20).

（责任编辑/浩天）

F224

A

1002-6487（2011）05-0031-02

教育部重大招标课题（08JD0015）；北京市教委重点课题（09BaJG245；SZ200910037013）