基于ARIMA模型的我国GDP分析预测
王正宇 王红玲
(安徽大学经济学院,安徽合肥230601)
一、有关时间序列分析的理论
时间序列分析,在预测一个时间序列未来的变化时,不再使用一组与之有因果关系的其他变量,而只是用该序列的过去行为来预测未来,不仅考察预测变量的过去值与当前值,同时对模型同过去值拟合产生的误差也作为重要因素进入模型,作为一种精确度相当高的短期预测方法,近年来在经济预测过程中广泛应用并取得了相当好的结果。
ARIMA模型是一类常见的随机时间模型,它是由美国统计学家博克斯和英国统计学家詹金斯于20世纪70年代提出来的,亦称B-J方法。其基本思想是将预测对象随时间推移而形成的数据序列视为一个随机序列,用一定的数学模型来近似描述这个序列。这个模型一旦被识别后就可以从时间序列的过去值及现在值来预测未来值。
Box-Jenkins方法在应用中的常见模型形式为:自回归移动平均模型(Autoregressive Moving Average Model,简记ARMA):若时间序列Yt为它的当前与前期的误差和随机项,以及它的前期值的线性函数:

则称该时间序列yt为自回归移动平均模型,记为ARMA(p,q)。参数 φ1,Λ,φp 为待估自回归参数,θ1,Λ,θq为待估移动平均参数,残差μt为白噪声序列。显然,AR(p)模型和MA(q)模型都是ARMA(p,q)模型的特例。Box-Jenkins模型要求时间序列为平稳序列,而实际应用中时间序列往往表现为长期趋势,季节变动、循环变动的非平稳数列,这时可通过差分法反复差分以消除其趋势,于是上述ARMA(p,q)又经常以自回归移动求积平均模型(Autoregressive Integrated Moving Average Model,简记ARIMA)的形式加以标记。其模型符号为ARIMA(p,d,q),p代表自回归阶数d,表示对非平稳数列进行差分处理的次数,q代表移动平均的阶数。
该方法把时间序列建模表述为三个阶段:
第一,模式识别:确定时间序列应属的模型类型,其基本原理是根据数据的相关特性进行鉴别;
第二,估计模型的参数,并结合定阶准则和残差检验对模型的适用性进行诊断检验;
第三,应用模型进行预测。
二、基于ARIMA模型分析预测中国国内生产总值(GDP)
从中国统计局统计年鉴上摘录的1978—2008年中国GDP(生产法)依次如下(单位:亿元):

从数据的散点图上来看,我国GDP对时间折线图序列表现出趋势性,经验判断是不平稳的。
方法上序列的平稳性可以用自相关分析图(自相关函数ACF图和偏自相关函数PACF图)判断:如果序列的自相关系数AC很快地(滞后阶数K大于2或3时)趋于0,即落入随机区间,时序是平稳的,反之非平稳。经过检验该序列非平稳。
也可以检验对所有k>0,自相关系数都为0的联合假设,这可通过如下Q统计量进行,该统计量近似地服从自由度为m的χ2分布(m为滞后长度)。因此,如果计算的Q值大于显著性水平为ɑ的临界值,则有1-ɑ的把握拒绝所有自相关系数同时为0的假设。若样本较小,则m一般取[n/4]。
从Q统计量的计算值看,滞后8期的计算值为71.83,超过5%显著性水平的临界值15.51拒绝所有相关系数都为0的假设。
在现实中,常见的时间序列多具有某种趋势,但许多序列通过差分可以平稳。如果原序列非平稳,经过d阶逐期差分后平稳,则新序列称为齐次序列。平稳序列可以建立ARMA(p,q)模型。原序列可表示为ARIMA(p,d,q)模型。判断时间序列的趋势是否消除,只需考察经过d阶差分后序列的自相关序列图,自相关系数是否很快趋于0。
首先进行一阶差分,经过一阶差分的序列仍然不平稳。因此需要继续差分。
进行二阶差分后,对二阶差分GDP做ADF检验,以检验序列是否有单位根,即是否非平稳,二阶差分后的序列ADF单位根检验结果证实了它的平稳性。
模型的识别与建立:
在需要对一个时间序列运用B-J方法建模时,应运用序列的自相关与偏自相关对序列适合的模型类型进行识别,确立 p,q。
参看二次差分后的自相关序列图,自相关系数在k=1和k=3时显著不为0,可以考虑q=1,2,3。同理偏自相关系数在k=1和k=3时显著不为0,可以考虑p=1,2,3。
综上,序列 ddgdp可以建立 ARMA(1,1)或 ARMA(1,2)或 ARMA(2,1)或 ARMA(2,2)或 ARMA(3,1)或ARMA(1,3)或 ARMA(3,2)或 ARMA(2,3)或 ARMA(3,3)。经过筛选对比,将ARMA(p,q)模型的滞后多项式倒数根落入单位圆外的模型排除,仅考虑ARMA(1,2)和ARMA(2,3)。对序列 gdp 来说就是 ARIMA(1,2,2)和ARIMA(2,2,3)。
对ARIMA(1,2,2)模型建立本文通过Eviews软件采用命令方式,在主窗口命令行输入
ls d(gdp,2,0)ar(1)ma(1)ma(2)
这里,对参数t检验显著性水平的要求并不像回归方程中那么严格,更多的是考虑模型的整体拟合效果。调整后的决定系数、AIC和SC准则都是选择模型的重要标准。
再建立 ARIMA(2,2,3)模型:

经过比较,ARIMA(2,2,3)模型t检验更加满足显著性水平,同时调整后的决定系数也大了不少,AIC和SC准则值比前面模型更小,说明这个ARIMA(2,2,3)模型是更适合的。

参数估计后,应该对ARIMA模型的适合性进行检验,即对模型的残差序列进行白噪声检验。若残差序列不是白噪声序列,意味着残差序列还存在有用信息没被提取,需要进一步改进模型。通常侧重于检测残差序列的随机性,即滞后期k>0,残差序列的样本自相关系数应近似为0。检测方法可以通过观察样本自相关序列图:对ARIMA(2,2,3)模型从k=8这行找到检验统计量Q值为1.5323,从Prob列得到值为67.5%,拒绝原假设犯错的概率为67.5%,即残差序列相互独立为白噪声的概率很大。因此检验通过,残差序列是纯随机的。

从拟合回归图看拟合图形的趋势走向和幅度较为一致。
基于序列 ARIMA(2,2,3)模型我国2007—2011年GDP预测值
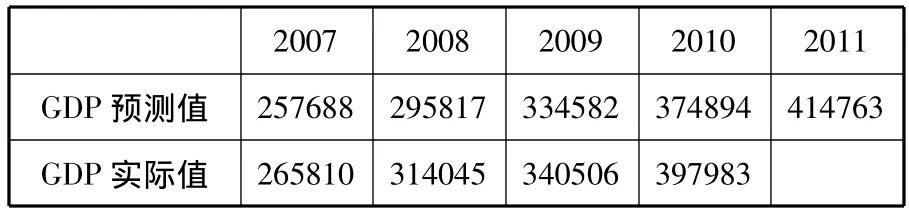

三、结论
本文利用ARIMA模型对我国经济进行了预测与分析,实证分析表明,该模型对于分析及预测我国GDP是简单而又非常有效的。从图中MAPE项可以看出与实际值预测值(2007、2008两年)之间误差百分比是比较小的。另外值得注意的是,ARIMA模型一般在短期内的预测比较准确,随着预测的延长,三年以上预测误差相对增大,这也是ARIMA模型的一个缺陷。但尽管如此,如果在建立模型过程中不断补充近期数据,调整和优选新模型并实现动态预测,则预测效果还可进一步提高,与其它的预测方法相比,其预测的准确度还是比较高的。同时,这里采用的Box-Jenkins建模思想,由于不需要对时间序列的发展模式作先验的假设,方法本身又可反复识别修改,直到获得满意的模型,因此非常适合各种经济时间序列,包括在辨别序列资料的典型特征十分困难和复杂情况下的预测。
[1]易丹辉.统计预测方法与应用[M].中国统计出版社,1988.
[2]李子奈.计量经济学[M].北京:高等教育出版社,2000.
[3]古亚拉提.经济计量学精要[M].机械工业出版社,2006.
[4]易丹辉.数据分析与Eviews应用[M].中国统计出版社,2002.

