Rayleigh面波各阶模式频散曲线对横波速度和层厚的敏感性探讨

张明财，熊章强，张大洲，刘白璐

(中南大学 信息物理工程学院，湖南长沙410083)

Rayleigh面波各阶模式频散曲线对横波速度和层厚的敏感性探讨

张明财，熊章强，张大洲，刘白璐

(中南大学 信息物理工程学院，湖南长沙410083)

Rayleigh面波勘探的目的在于有效利用频散曲线反演地层厚度及横波速度，而不同模式的频散曲线对横波速度和层厚的敏感性不同。通过求取介质参数变化10%后与参数不变化时的二组频散曲线的差值，得到各阶模式的频率～相速度差曲线，分析了Rayleigh面波各模式频散曲线对横波速度、层厚的敏感性。试验结果表明，基阶模式对于浅层的横波速度和层厚比较敏感，敏感区域主要集中在较窄的频带范围内。而高阶模式对于相对较深层的横波速度和层厚比较敏感，且频率范围分布较大，敏感性强的频段分布比较分散。研究结果可以为Rayleigh面波多模式联合反演提供理论依据。

Rayleigh面波频散曲线;横波速度;层厚;敏感性

作者在本文以三层速度递增模型为例，从频率－相速度差的角度，分析探讨了Rayleigh面波各阶模式频散曲线对横波速度和地层层厚的敏感性。其具体分析方法为:首先利用快速标量传递矩阵算法(凡友华［16])计算出给定模型的频散曲线，然后将其中一个介质参数改变10%，而其余参数不变，再次计算出参数变化后的频散曲线，将二次计算出的对应的各阶模式相减，即得到频散曲线各阶模式的频率～相速度差曲线。频率～相速度差曲线能够很好地反映参数变化前后各阶模式的频散曲线的变化，即各阶模式对于变化的参数的敏感性。

1 对横波速度的敏感性

SNazarian［17]认为，均匀层状介质中Rayleigh面波的相速度，是频率和四个地层参数，即横波速度、纵波速度、层厚、密度的非线性函数，可用隐函数方程表示为:

式中fj表示第j个频率;VRmj表示第j个频率，第m阶模式的相速度;VS=(vs1，vs2，…，vsn)T表示横波速度向量，其中vsi表示第i层的横波速度，n表示模型层数;VP=(vp1，vp2…，vpn)T、ρ=(ρ1，ρ2，…，ρn)T、H=(h1，h2，…，hn－1)T分别表示纵波速度向量、密度向量、层厚向量。

在给定频率及地层参数后，就可通过方程(1)求解出Rayleigh面波频散曲线。

由于快速标量算法具有稳定性好，计算速度快，精度高的特点，作者采用该方法计算频散曲线。取如表1所示的模型参数，由快速标量传递矩阵法计算得频散曲线如图1所示。从图1可见，随着频率的增加(波长减小)，Rayleigh面波各阶模式的频散曲线趋于表层的横波速度。

表1 三层模型参数Tab．1 Three layersmodel parameter

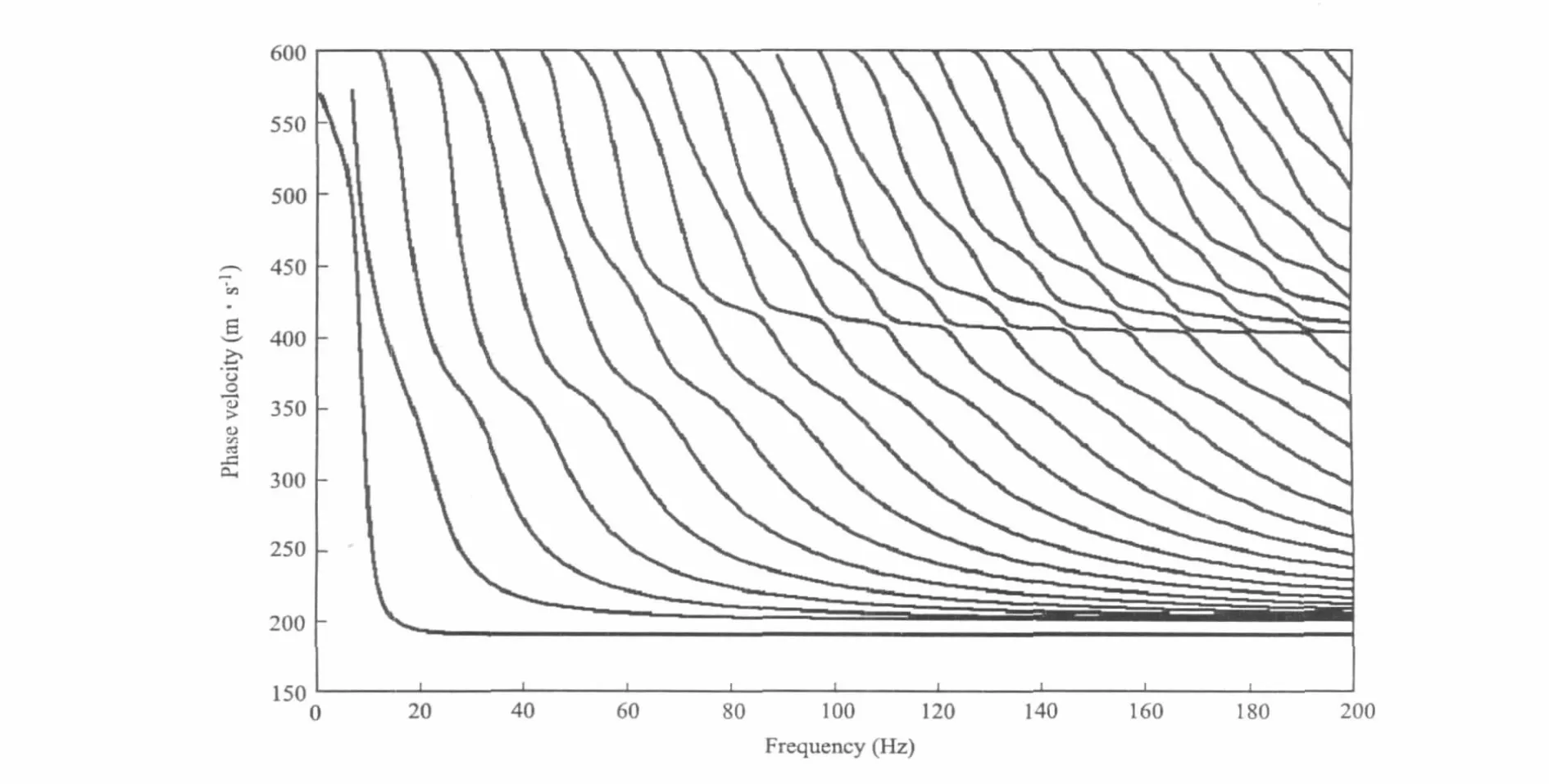
图1 三层模型频散曲线Fig．1 Dispersion curve of three layersmodel

1．1 第一层横波速度变化

将第一层的横波速度增大10%(即变为220 m/s)，其它的参数不变，仍采用快速标量传递矩阵法计算出其频散曲线，由式(2)计算各阶模式的相速度差异，即将各阶模式的各个频率对应的相速度值相减，得到第一层的横波速度变化后频散曲线各阶模式的频率～相速度差曲线如图2所示(为方便展示，只取基阶模式和1阶～4阶高阶模式)。

分析图2中各阶模式的频率～相速度差曲线可知:当第一层横波速度发生变化时，基阶模式对低频段(约7 Hz～13 Hz)的相速度比较敏感。其它各阶模式对第一层横波速度的敏感区段比较宽，呈驼峰状，出现两个峰值:第一高阶模式的两个峰值区段分别为10 Hz～16 Hz和18 Hz～28 Hz;第二高阶模式的两个峰值区段分别为16 Hz～23 Hz和32 Hz～47 Hz;第三高阶模式的两个峰值区段分别为26 Hz～36 Hz和46 Hz～63 Hz;第四高阶模式的两个峰值区段分别为32 Hz～48 Hz和60 Hz～85 Hz。随着模式的升高，相速度差第一个峰值对应的频率依次升高。且随着频率的增加，各阶模式的相速度差峰值交替出现，即依次出现基阶模式相速度差第1个峰值，第一高阶模式第1个峰值，第二高阶模式第1个峰值，第一高阶模式第2个峰值，第三高阶模式第1个峰值，第二高阶模式第2个峰值，第四高阶模式第1个峰值，第三高阶模式第2个峰值，第四高阶模式第2个峰值。随着频率的增大，各阶模式的相速度差先后都趋于恒定值20 m/s。

1．2 第二层横波速度变化

将表1模型参数中第二层横波速度(400m/s)增加10%，即变为440 m/s后，再由式(1)计算出第二层横波速度变化10%后的频散曲线各阶模式的频率～相速度差曲线，如图3(见下页)所示。对比图2、图3不难发现，各阶模式的相速度差的最大值明显减小(第一层横波速度变化10%时，相速度差趋于20 m/s，相速度差最大值大于80 m/s，而第二层横波速度变化10%时，各阶模式的相速度差趋于0 m/s，相速度差最大值小于35 m/s)，且频率范围也变窄(基阶模式频率范围变为7 Hz～11 Hz，第一高阶模式频率范围变为12 Hz～23 Hz，第二高阶模式频率范围变为13 Hz～33 Hz，第三高阶模式频率范围变为28 Hz～48 Hz，第四高阶模式频率范围变为30 Hz～60 Hz)。

1．3 第三层横波速度变化

图2 第一层横波速度变化10%时各阶模式频率～相速度差曲线Fig．2 Frequency－phase velocity difference curve with the shear velocity of the first layer 10%changed

图3 第二层横波速度变化10%时各阶模式频率～相速度差曲线Fig．3 Frequency－phase velocity difference curve with the shear velocity of the second layer 10%changed

图4 第三层横波速度变化10%时各阶模式频率～相速度差曲线Fig．4 Frequency－phase velocity difference curve with the shear velocity of the third layer 10%changed

将表1模型参数中第三层横波速度(600m/s)增加10%，即变为660 m/s后，由式(1)计算出第三层横波速度变化10%后的频散曲线各阶模式的频率～相速度差曲线，如图4(见下页)所示。随着频率的增大，各阶模式的相速度差曲线急剧衰减;随着阶次的增高，各阶模式的相速度差依次趋于恒定值0 m/s;随着深度的增加，各阶模式的频散曲线对相速度的敏感区段向低频段推移(第一层横波速度变化时，频率高达100 Hz时，各阶模式的频率～相速度差曲线尚未全部趋于恒定值;第二层横波速度变化时，频率为80 Hz时，各阶模式的频率～相速度差曲线全部趋于恒定值;第三层横波速度变化时，频率为40 Hz时，各阶模式的频率～相速度差曲线已经全部趋于恒定值)。

2 对层厚的敏感性

2．1 第一层层厚变化

将表1模型参数中第一层的层厚(10 m)增加10%，即变为11 m后，由式(1)计算出第一层的层厚变化10%后的频散曲线各阶模式的频率～相速度差曲线，如图5(见下页)所示。与第一层横波速度变化时的各阶模式的频率～相速度差曲线相似，基阶模式对低频段(约6 Hz～12 Hz)的相速度比较敏感，其它各阶模式对第一层横波速度的敏感区段比较宽，呈驼峰状，出现两个峰值。第一高阶模式的两个峰值区段分别为6 Hz～9 Hz和18 Hz～26 Hz;第二高阶模式的二个峰值区段分别为13 Hz～19 Hz和29 Hz～41 Hz;第三高阶模式的二个峰值区段分别为23 Hz～33 Hz和40 Hz～57 Hz;第四高阶模式的二个峰值区段分别为30 Hz～42 Hz和50 Hz～74 Hz。随着模式的升高，相速度差第一个峰值对应的频率依次升高。且随着频率的增加，各阶模式的相速度差峰值交替出现。

2．2 第二层层厚变化

将表1模型参数中第二层的层厚(10 m)增加10%，即变为11 m后，由式(1)计算出第二层的层厚变化10%后的频散曲线各阶模式的频率～相速度差曲线，如图6所示。类似于横波速度变化时的情形，各阶模式的相速度差的最大值明显减小(第一层的层厚变化10%时，相速度差最大值大于60 m/s，而第二层的层厚变化10%时，相速度差最大值小于15 m/s)，频率范围也变窄(基阶模式频率范围变为7 Hz～9 Hz，第一高阶模式频率范围变为7 Hz～17 Hz;第二高阶模式频率范围变为11 Hz～26 Hz;第三高阶模式频率范围变为20 Hz～32 Hz;第四高阶模式频率范围变为28 Hz～40 Hz)。同时随着深度的增加，各阶模式的频散曲线对相速度的敏感区段向低频段推移(第一层的层厚变化，频率高达100 Hz时，各阶模式的频率～相速度差曲线尚未全部趋于恒定值;而第二层的层厚变化，频率为50 Hz时，各阶模式的频率～相速度差曲线已经全部趋于恒定值)。

图5 第一层层厚变化10%时各阶模式频率～相速度差曲线Fig．5 Frequency－phase velocity difference curve with the depth of stratum of the first layer 10%changed

图6 第二层层厚变化10%时各阶模式频率～相速度差曲线Fig．6 Frequency－phase velocity difference curve with the depth of stratum of the second layer 10%changed

3 结论

(1)对比图2和图4;图3和图5可知:在同一地层中，Rayleigh面波各阶模式的频散曲线对横波速度和层厚的敏感性的频带分布特征相似。总体上，对横波速度的敏感性强于对层厚的敏感性，且随着层数的增加，对横波速度的敏感性比对层厚的敏感性增强。

(2)在表层，Rayleigh面波各阶模式对深层的横波波速和层厚的敏感性，随着频率的变化而起伏变化。频率～相速度差曲线的单调区间较多，随着层数的增加，起伏程度变弱，频率～相速度差曲线的单调区间减少，最底层横波速度变化后，频率～相速度差曲线在截至频率处便开始迅速衰减，最后趋于0 m/s。

(3)基阶模式的频散曲线在低频范围内比较敏感，且敏感的频带范围较窄。如果单纯地只利用基阶模式反演频散曲线，势必会损失高频范围内的信息，增加高频范围内的不确定性，使反演工作很难开展。相对地，高阶模式的敏感性强的频率范围分布比较大，且都分布在较高的频率范围内。基阶模式和高阶模式联合反演，可以减少频散曲线分析时参数的不确定性，减少反演的多解性，提高反演结果的精度。

［1]梁志强，邓道静．基于多阶模式的面波技术应用探讨［J]．勘探地球物理学进展，2008，31(4):253．

［2]杨成林．瑞雷面波勘探［M]．北京:地质出版社，1993．

［3]张碧星，鲁来玉．层状半空间中导波的传播［J]．声学学报，2002，27(4):295．

［4]SHUANG X．ZHANG，LUNG S．CHAN．Possible effects of misidentified mode number on Rayleigh wave inversion［J]．Journal of Applied Geophysics，2003(53):17．

［5]肖伯勋．高模式瑞雷面波及其正反演研究［D]．长沙:中南大学博士论文，2000．

［6]JIANGHAI XIA，YIXIAN XU，CHAO CHEN et al．Simple equations guide high－frequency surface wave investigation techniques［J]．Soil Dynamics and Earthquake gineering，2006(26):395．

［7]杨天春，何继善，吕绍林，等．三层层状介质中的多导波模式及其频散和位移特征［J]．物探化探计算技术，2004，26(1):20．

［8]杨天春，何继善，吕绍林，等．三层层状介质中瑞利波的频散曲线特征［J]．物探与化探，2004，28(1):41．

［9]柴华友，吴慧明，张电吉．弹性介质中表面波理论及其在岩土工程中应用［M]．北京:科学出版社，2008．

［10]JIANGHAIXIA，RICHARD D．MILLER，CHOON B．PARK．Estimation of near－surface shear－wave velocity by inversion of Rayleigh waves［J]．Geophysics，1999，64(3):691．

［11]JIANGHAIXIA，RICHARD D．MILLER，CHOON B．PARK．Advantages of calculating shear－wave velocity from surface waves with higher modes［C]．70thAnnual Meeting，Calgary，Canada，Society of Exploration Geophysicists，Tulsa，2000:1295．

［12]JIANGHAIXIA，RICHARD D．MILLER，CHOON B．PARK，et al．Inversion of high frequency surface waves with fundamental and highermodes［J]．Journal of Applied Geophysics，2003(52):45．

［13]XIA J，XU Y，CHEN C，et al．Simple equations guide high－frequency surface－wave investigation techniques［J]．Soil Dynamics and Earthquake Engineering，2006(26):395．

［14]YINHE LUO，JIANGHAI XIA，JIANGPING LIU，et al．Joint inversion of high－frequency surface waves with fundamental and highermodes［J]．Journal of Applied Geophysics，2007(62):375．

［15]罗银河，夏江海，刘江平，等．基阶与高阶瑞利波联合反演研究［J]．地球物理学报，2008，51(1):242．

［16]凡友华，肖柏勋，刘家琦．计算层状介质中轴对称柱面瑞利面波频散函数的δ矩阵法［J]．物探与化探，2001，25(2):109．

［17]NAZARIAN S．In situ Determination of Elastic Moduli of Soil Deposits and Pavement Systems by Spectral Analysis of Rayleigh Waves Method［D]．Dissertation，University of Texas，Austin，1984．

P 315．9

A

1001—1749(2011)02—0153—06

0 前言

“十一五”国家科技支撑项目(2006BAC07B00)

2010－08－12

张明财(1986－)，男，硕士，主要研究方向:瑞雷面波正反演研究。

Rayleigh面波凭借其衰减小，信噪比高，抗干扰能力强，分辨率高，在层状介质中所具有的频散特性以及传播速度，与介质的物理力学性质有密切关系，在工程勘察和无损检测中有着广泛的应用［1、2]。Rayleigh面波勘探的目的在于有效利用频散曲线，反演地层厚度及横波速度。传统的频散曲线反演都是基于基阶模式的，没有充分利用高阶模式的频散曲线，导致反演结果不甚理想。张碧星等［3]研究了层状介质中Rayleigh面波的能量分布，并得出结论:Rayleigh面波的能流密度随深度的增加而很快衰减，能量分布在各阶模式中，在某些频率范围内，高阶模式的能量强于基阶模式。这表明，以能量高低为标准提取的频散曲线，并不一定是基阶模式的频散曲线。X Shuang等［4]特别指出:Rayleigh面波的模式识别错误，可能会影响到反演结果的错误。肖伯勋［5]对高模式的Rayleigh面波进行了研究后认为:高模式Rayleigh面波对地层参数变化的敏感性，较之基阶模式波要强得多。在不同地层参数条件下获取的Rayleigh面波的基阶模式可能很相似，但高阶模式的频散曲线会有明显差别。在分层介质中，Rayleigh面波具有多个模式，由于截止频率［6、8]的存在，模式数量会随着频率的增加而增多。杨天春［7、8]分析了不同类型的三层层状介质中的Rayleigh面波频散曲线的特征后认为:位移的激发强度与声波的频率密切相关，不同模型接收到的导波模式不同，且各个导波的相速度曲线之间不相交。一般地，基阶模式沿介质深度方向衰减较快，影响深度约为一个波长，而波长越长，穿透深度越深。在频率相同的情况下，高阶模式的相速度高于基阶模式的相速度，而其波长比基阶模式的波长长，因此高阶模式的穿透深度较深，对较深层传播介质的横波速度和层厚比较敏感。在不同分层中，部份模式频散在某一频率范围内可能是接近的，甚至是相同的。在某一频率范围内，某些阶次的模式频散曲线对分层参数(横波速度、层厚)的变化并不敏感［9]。XIA Jiang－hai等［10]研究发现:地层的纵波速度和密度，只对频散曲线的基阶模式的高频部份有影响，在实际的频散曲线反演过程中，可将地层的纵波速度和密度视为误差高达25%的常数，仅考虑地层厚度和横波速度。XIA Jiang－hai等［11～13]联合基阶模式和第一高阶模式的频散曲线，对Rayleigh面波进行了反演，增加了反演结果的可靠性，减少了反演的多解性。罗银河等［14、15]利用Jacobian矩阵Js研究了Rayleigh面波基阶模式和第一高阶、第二高阶模式的频散曲线，对横波速度的敏感性，并联合基阶模式和第一高阶、第二高阶模式的频散曲线进行反演，增强了反演的稳定性，提高了反演的精度。