高压小流量稳流型调节器特性研究
陈维宇,程亚威,李小明,张赤民
(西安航天动力研究所,陕西西安710100)
0 引言
在现代高压补燃液体火箭发动机中,为了提高发动机工作过程的精度和保持工况以及能使主要参数 (推力、混合比)能按一定的规律变化,在发生器燃料路设置了稳流型流量调节器(以下简称调节器),以保证发动机的主级工况稳定;同时,调节器作为发动机最主要的执行机构,其工作性能的高低直接影响到发动机工作状态的好坏。该调节器流量小,工作压降范围宽,调节精度要求高。为此研制了一种能适应发动机工作要求的调节器。目前国内外常用的流量调节器有直接作用式和间接作用式调节器。该调节器采用了直接作用式结构,结构简单,性能稳定可靠。本文结合调节器的研制,叙述了该调节器的结构,对影响其性能的因素进行了分析,给出了试验结果。
1 调节器的结构及工作原理
在液体火箭发动机中,调节器采用的结构形式主要有两类:直接作用式和间接作用式。根据发动机对调节器的功能要求、技术指标要求,采用了直接作用式调节器结构方案。
1.1 调节器结构
调节器结构示意图见图1,主要由壳体1、齿套2、齿轮轴3、调节弹簧4、导向套5、活塞环6、滑阀7、滑阀座8等零件组成;第一级节流副位于导向套上,第二级节流副位于滑阀座上。
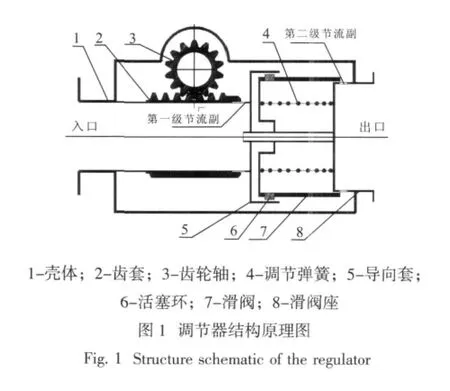
1.2 调节器工作原理
调节器是利用反馈原理进行工作的。作用在敏感面积上的压力方向始终与滑阀关闭的方向一致,而弹簧力则是朝向滑阀打开的方向,通过对作用于敏感面积上的压差力与弹簧力、摩擦力等进行比较,控制第二级节流副的遮盖量,来保持第一级节流副压降基本不变。其工作过程如下:假设入口压力增加,而出口压力不变时,则作用于敏感面积前后的压差增加,滑阀的平衡受到破坏,使滑阀朝关闭方向移动,从而第二级节流副流阻增大,这样导致调节器的内腔压力增加,反过来又使敏感面积前后的压差减小,抑制滑阀继续朝滑阀关闭方向移动,最终使作用于滑阀上的力处于平衡状态,保持第一级节流副压差基本不变;反之,入口压力降低,出口压力不变时,则作用于敏感面积上的压差也减小,滑阀朝打开方向移动,使第二级节流副流阻减小,这样调节器的内腔压力降低,反过来又使作用于敏感面积上的压差增加,抑制滑阀继续朝滑阀打开方向移动,最终使作用于滑阀上的力处于平衡状态,保持第一级节流副压降基本不变。同理,当入口压力不变,出口压力变化时,作用于敏感面积上力的平衡被破坏,通过反馈作用,保持第一级节流副压降基本不变。
2 调节器的静态特性及影响因素分析
静态特性包括流量特性和负载特性,流量特性反映的是控制特性,即调节器流量与外部控制信号的变化关系;而负载特性反映的是抗干扰能力,即在外部压降变化时调节器流量的变化关系,可用调节精度来衡量。
2.1 调节器静态方程及计算
2.1.1 调节器静态方程
调节器的静态方程可由流量平衡、压力平衡及力平衡方程得出,调节器的静态特性由下列方程构成:
1)流量方程
a.第一级节流副流量
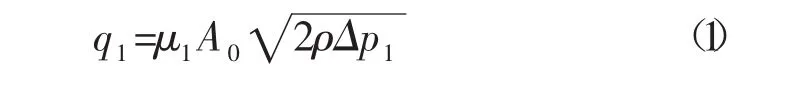
式中:q1为第一级节流副流量,kg/s;μ1为第一级节流副流量系数,无量纲系数;A0为第一级节流副过流面积,m2;ρ为介质密度,kg/m3;Δp1第一级节流副压降,Pa。
b.第二级节流副流量
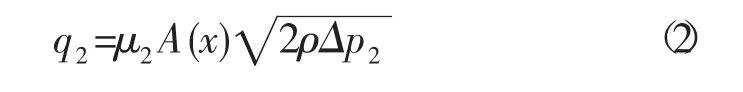
式中:q2为第二级节流副流量,kg/s;μ2为第二级节流副流量系数,无量纲系数;A(x)为第二级节流副过流面积,m2;ρ为介质密度,kg/m3;Δp2为第二级节流副压降,Pa。
c.环形缝隙流量
在调节器结构中,对调节器性能产生影响的还有3处泄漏通道:活塞环与导向套、滑阀与滑阀座、滑阀与滑阀座杆。由于环形泄漏通道的间隙很小,雷诺数Re小于一定值时,流体处于层流状态,根据工程经验,通过环形泄漏通道的流量qml:
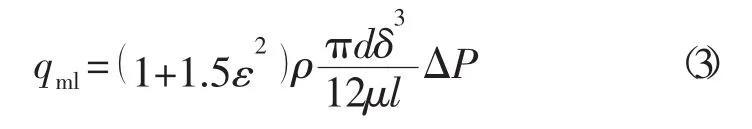
式中:qml为环形泄漏通道的泄漏量,kg/s;l为环形泄漏通道长度,m;ρ为介质密度,kg/m3;Δp为环形泄漏通道压降,Pa,ε为偏心率,无量纲系数;μ为介质的动力粘度,Pa·s;δ为环形泄漏通道的径向配合间隙,m;d为环形泄漏通道直径,m。
根据方程3,通过活塞环、滑阀与滑阀座的环形泄漏通道的流量:
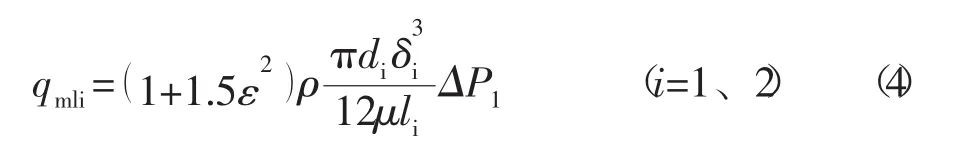
式中的符号与公式(3)意义相同,下标表示不同的泄漏位置;
d.第二级节流副泄漏通道的流量:
式中:qml3为第二级节流副泄漏通道的泄漏量,kg/s;μ3为第二级节流副流量系数,无量纲系数;ρ为介质密度,kg/m3;Δp2为第二级节流副压降,Pa;δ3为第二级节流副泄漏通道的径向配合间隙,m;l3为第二级节流副遮盖部分三角形孔周长,m;N为三角形窗口数量
2)滑阀的作用力平衡方程
式中:A为敏感面积,m2;x为第二级节流副的遮盖量,m;x0为调节弹簧预压缩量,m;K为调节弹簧刚度,N/m;Fm为滑阀运动时的摩擦力,N;FT为液动力,N。
液动力计算方程:
式中:δk为滑阀刃边厚度,m;H(x)为第二级节流副节流处的滑阀边缘长度,m。
3)流量连续方程
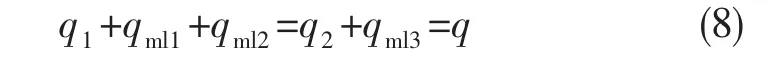
式中:q为调节器入口、出口流量,kg/s。
4)第二级节流副的流通面积
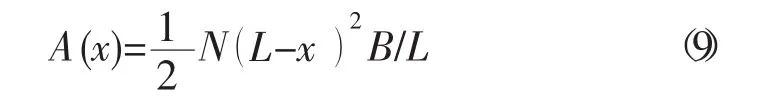
式中:A(x)为第二级节流副过流面积,m2;B为三角形窗口底边长,m;L为三角形窗口高度,m。
5)压力平衡方程

式中:Δp为调节器总压降,Pa;
根据方程(1)~(10)通过迭代计算可以确定在某一额定流量下,调节器流量与压降的关系,从而可以得出调节器的调节精度。
2.1.2 静态误差分析
为确定调节器的静态误差,对方程(1),(3),(4),(6)进行微分,可以得到:
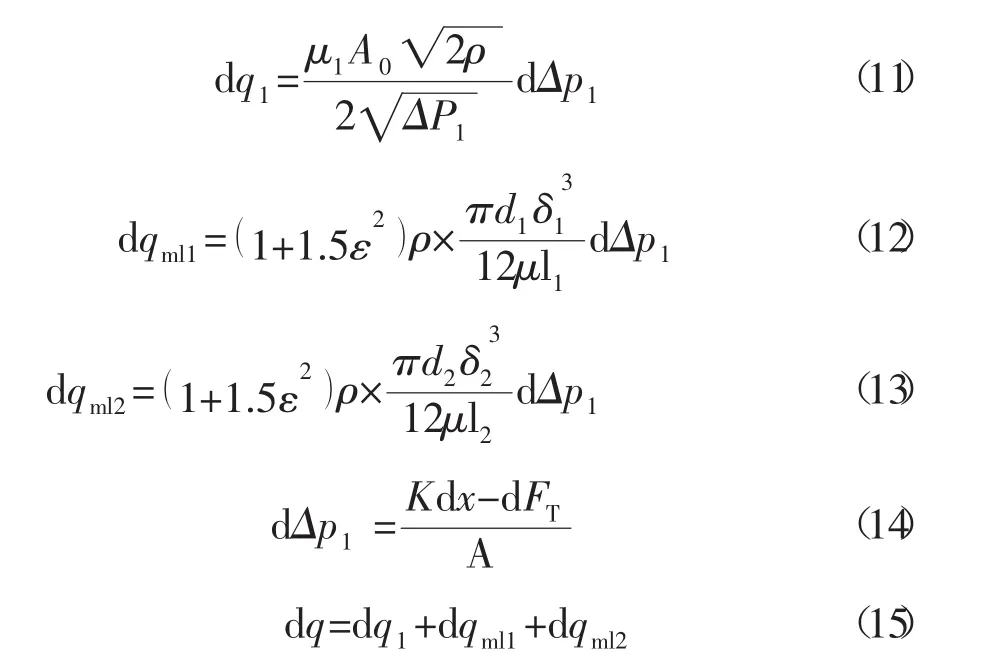
由 方 程 (3),(4),(5),(13),(14),(15),(16),(17)可以推出
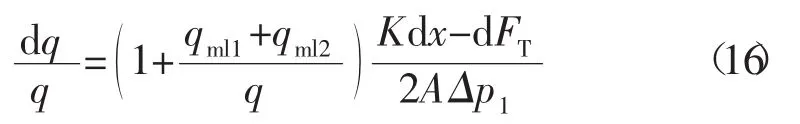
从方程(16)即可确定调节器的静态误差。在水流量为0.63 kg/s时,根据方程(16)计算出的调节器压降在3 MPa和9 MPa时的静态误差分别为-1.35%和+1.02%。
2.2 调节器静态性能的影响因素分析
从方程(16)可知,调节器的调节精度主要与敏感面积、调节弹簧刚度、第一道节流窗口压降的选取及工作压降范围内第二道节流窗口的行程、泄漏量、作用于滑阀上的流体动力,摩擦力及环形泄漏通道的流量等因素有关。
从方程(16)可以看出,在入口流量一定的情况下,泄漏通道的流量增加,则第一级节流副主流道的流量减小,静态误差增大。流量越小,静态误差将越大;同时,第二级节流副的泄漏通道流量越大,则使主流道的流量变小,第二节流副面积减小,滑阀位移增量增加,也使静态误差增大。另外,第一级节流副的泄漏通道的泄漏量还对调节器的流量特性有一定影响。
对不同介质,其动力粘度、密度是不同的。从方程(3)可以看出,泄漏量与动力粘度成反比,与密度成正比。以水和煤油为例,水的动力粘度比煤油低,而密度比煤油高,因此,煤油通过环形缝隙中泄漏量比水小;另外由于通过滑阀的泄漏量小,滑阀位移变化量也减小。因此,根据方程(16),以煤油为介质时,其调节精度比水高。
综上所述,影响调节器静态性能的因素很多,调节器的静态误差是各种因素共同作用的结果,设计时不能仅单纯考虑某一因素的影响;此外,这些因素往往还与调节器动态特性有关,因此须对各种因素进行综合考虑。
3 试验验证
3.1 静态试验
对所研制的调节器产品进行了液流试验,试验表明:调节器的水流量可以在0.2~0.8 kg/s范围内进行调节,流量与角度基本呈线性关系(见图 2)。
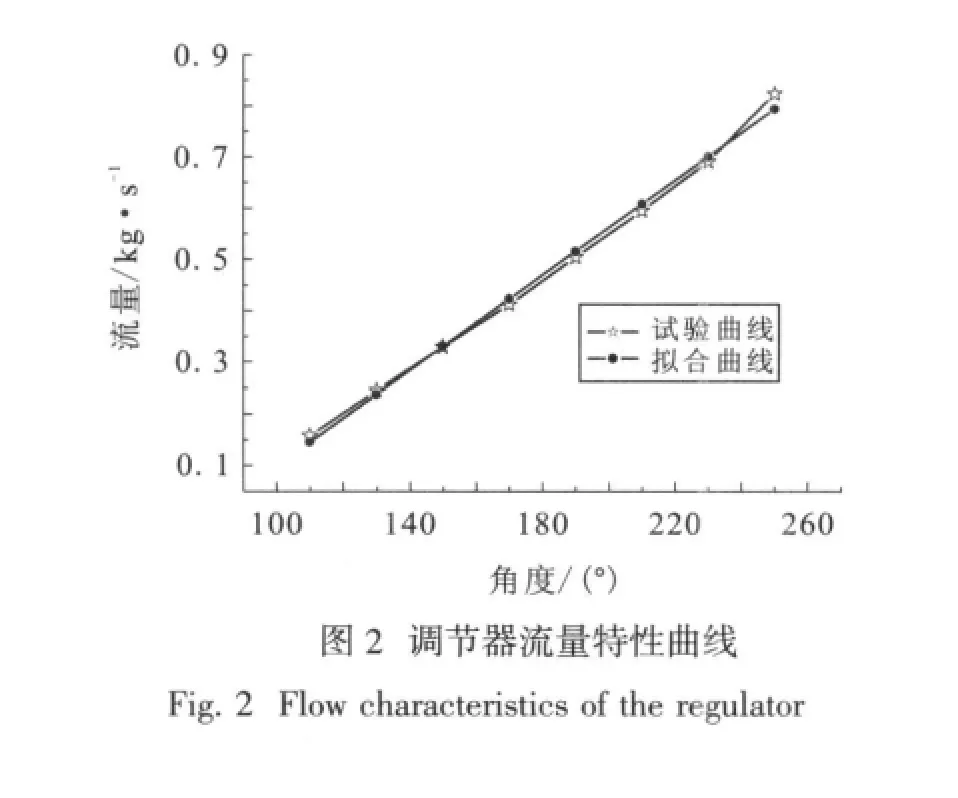
由于制造误差和第一级节流副压降变化等因素引起的误差对流量特性的影响不大,拟合曲线与试验曲线的线性度相关系数在0.998以上。水流量在0.3~0.63 kg/s时,压降为3~11 MPa范围,流量均能保持稳定,静态误差在±2%以内,试验曲线见图3。计算结果与试验结果比较一致性较好。
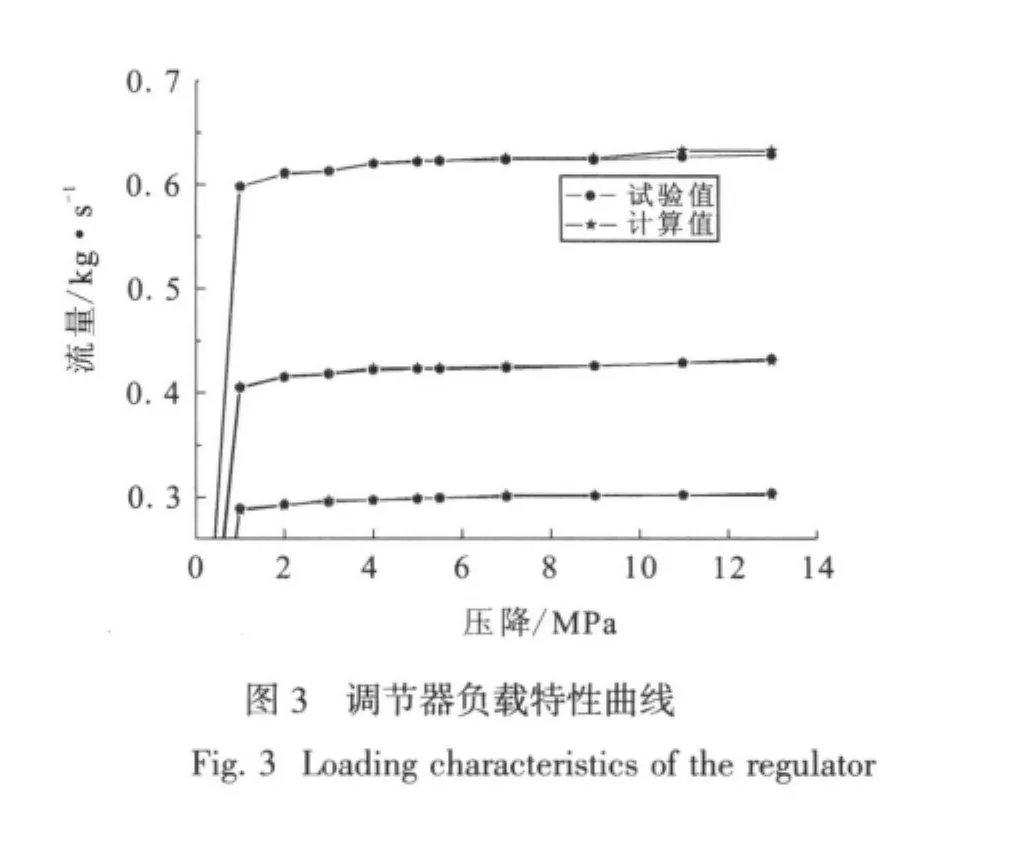
3.2 调节器的加载特性
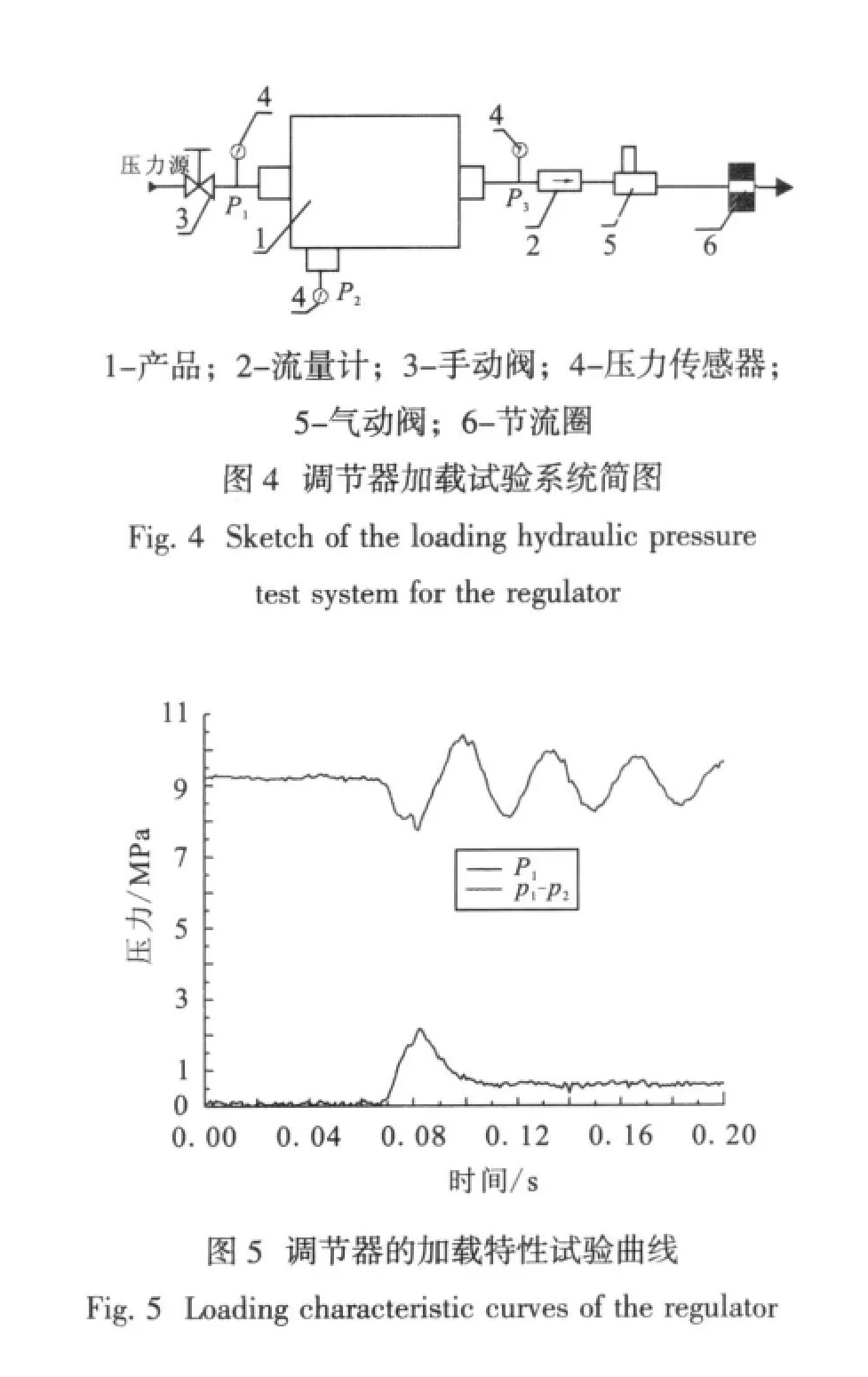
调节器的加载特性是指调节器的压降由零突然增加至某一压降下的其流量响应特性,反映的是调节器调节特性,可以通过第一级节流副压降的变化反映出来。这是一个动态过程,即滑阀由静止到运动,然后再稳定的过程,其目的是模拟发动机启动时调节器的工作特性。当调节器压差为零时,在弹簧力作用下,第二级节流副处于最大开度,随着出口阀门快速打开,滑阀来不及响应,这时会产生很高的峰值流量。在发动机起动时,随着调节器出口阀门的打开,调节器压降发生变化,调节器流量也随之变化。加载特性试验系统见图4。
从试验曲线(见图5)可以看出调节器第一级节流副(p1-p2)的变化趋势,随着调节器压降的增加,第一级节流副的压降(p1-p2)迅速增加,并伴有一峰值,峰值流量约为稳定调定流量的2倍(调节器流量的变化趋势可以从第一级节流副的压力变化情况反映出来),随后开始下降,共经过约40 ms后流量趋于稳定。
4 结论
对所研制的调节器进行了计算分析并通过液流试验验证,可以得出以下结论:
1)调节器的调节精度小于2%,水流量可在0.2~0.8 kg/s范围进行调节;
2)对影响调节器调节精度的主要因素进行了分析,认为对小流量调节器而言,内部流道的泄漏量是影响其性能的一个重要因素。
[1]张贵田.高压补燃液氧煤油发动机[M].北京:国防工业出版社,2005.
[2][俄]格列克曼Б Ф.液体火箭发动机自动调节 [M].北京:宇航出版社,1995.
[3]液体火箭发动机设计[下][J].北京:宇航出版社,1994.
[4]陈维宇,刘站国,王昕,等.流量调节器研制中的主要问题及结构改进[J].火箭推进,2009,35(3):45-50.
[5][美]休泽尔D K.液体火箭发动机现代工程设计[M].朱宁昌,译.北京:宇航出版社,1993.
[6]ШЕВЯКОВ А А,КАЛНИН В М.Теория автоматического управления ракетными двигателями [M].DjVu,RUS:Иэд-во Машиностроение,1978.
[7]王昕.流量调节器动态特性研究 [J].火箭推进2004,30(3):19-24.
[8]赵双龙,许长华,魏超.滑阀液动力的计算与分析[J].火箭推进2006.32(3):18-23.
[9]李哲,魏志军,张平.自力式调压阀变开度流场及特性分析 [J].推进技术,2008(5):112-116.
[10]吕翔,刘佩进,何国强,等.火箭引射模态下一次火箭流量优化方法研究 [J].固体火箭技术,2010(6):37-41.
[11]朱森元.氢氧火箭发动机及其低温技术 [M].北京:国防工业出版社,1995.
[12]徐海军,潘存云,谢海斌,等.水下仿生推进器阀控液压摆动关节建模与动态特性分析 [J].国防科技大学学报,2010(6):120-125.

