超燃燃烧室内流场数值模拟研究

杜飞平，谭永华，陈建华

（1.西安航天动力研究所，陕西西安710100；2.航天推进技术研究院，陕西西安710100）

0 引言

高超声速飞行器是指飞行马赫数大于5.0的远程巡航飞行器,它综合了航空航天领域众多学科的新技术,代表了未来航空航天领域的研究发展方向,被认为是继隐身技术之后的又一重要技术领域。该飞行器主要由前体与进气道、燃烧室（含隔离段）、尾喷管与后体等部件组成。

由于高超声速飞行器在军事、政治和经济中的重要战略作用，各航空航天大国多年来从未间断过高超声速技术方面的研究；最近伴随着X-37B飞行试验的成功，高超声速飞行器的发展又进入了一个新的阶段。各种高超声速飞行器如高超声速导弹、高超声速飞机及空天飞机等具有速度快、反应时间短、突防能力强等特点。

随着世界各国对高超声速技术的日益重视，作为关键技术之一的超声速燃烧室内流场的研究显得越来越重要。本文开展了超燃燃烧室内一维和三维流场的研究，重点分析管内高速流动与燃烧相耦合的流场，拟初步研究吸气式高超声速飞行器内流场（包含隔离段和燃烧室内流场）的复杂流动结构，其间包含超、高超声速流动中的激波/激波相交、激波/附面层干扰、分离流、燃料射流以及漩涡结构等复杂结构，涉及到了气体动力学、化学反应动力学、燃烧学等多学科交叉。

1 超燃燃烧室内流场特性

“在高超声速流动和吸气式高超声速飞行器系统的理解和控制方面，真正的进步最终还是依靠分析和计算能力的提高”。作为吸气式高超声速飞行器关键技术的超声速燃烧的分析和计算至关重要。

为了从外部静压测量数据的分析中获得超声速燃烧内部流场性质的信息，也为了满足超燃燃烧室试验数据分析和处理的需要，William H.Heiser和David T.Pratt提出了一种超燃燃烧室一维物理模型（图1），基本上描述了超声速燃烧中的主要物理过程。在他们的模型中，燃烧室是由等截面的隔离段和带扩张角的燃烧段组成，其中发生的物理过程大致可以分为绝热压缩、等压释热和膨胀释热三个过程。

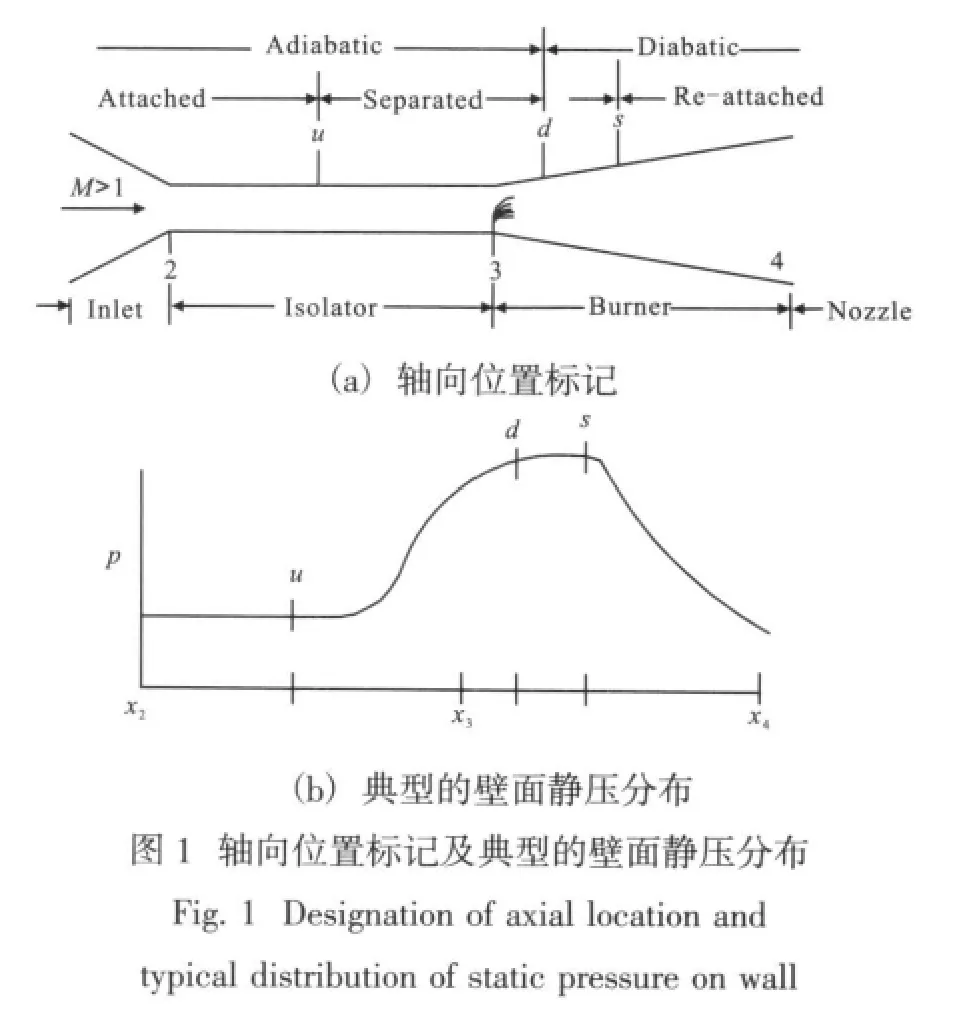
在该模型中，2，3和4为燃烧室在轴向的几何位置，分别表示隔离段进口、燃烧室进口和燃烧室出口；点u，d和s为流动状态位置，分别表示流动分离区起点、燃烧释热起点和流动分离区的终点；2～d为流动绝热区，d～4为燃烧释热区，u～s为流动分离区，2～u和s～4为附着和再附着流动区。

2 一维流场分析模型研究

在理解超声速燃烧的物理过程中，一维理论分析是超声速燃烧性能估算的一个有用的工具，它只考虑流动变量在气流方向的变化，分析过程大大简化。超燃燃烧室结构简单，基本上只有一个略有扩张的直通道，流动变量在每一个截面上大致均匀，且流动可视为定常，符合一维理论分析的假设。

在一维流场分析模型中选择两种模型进行研究。该两种一维流动分析模型的共同点在于：

1）忽略燃烧室壁面摩擦，燃料支板和燃烧喷射的阻力以及燃料喷入的质量增加；

2）通过试验给出燃烧释热点和流动分离再附着点的静压，人为给定其轴向位置；

3）分析中先求马赫数的分布，再求其他的变量。

2.1 模型一处理过程

在该模型中，超燃燃烧室流场被分为绝热压缩、等压燃烧以及非绝热再附着三段来处理。

2.1.1 起始的绝热压缩段 （x2～x）d

因为是绝热压缩，所以本段的特点是总温保持不变，即保持隔离段进口总温T0（xi）=T02。

用最小二乘法处理x2～xd区间的试验压力数据p（ xi）值，根据Waltrup和Billig的建议，u到d点的压强分布为一个三次多项式，形式如下

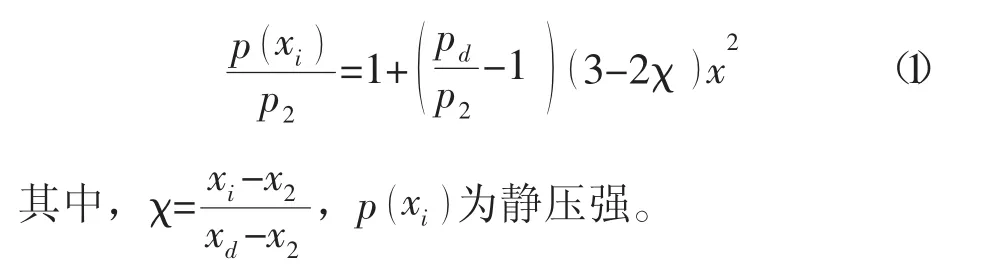
在绝热压缩段的过程中，流动发生了分离，此时隔离段流场的面积分成两部分，一部分是分离流面积，另一部分则是芯流面积。

根据一维流动理论，核心流的面积可表示为

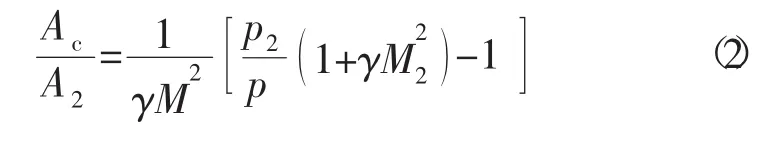
由于斜激波串的绝热压缩过程，燃烧室核心流的马赫数可以表示为

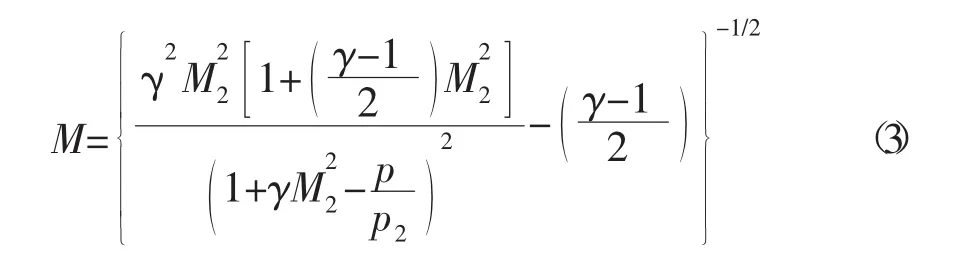
式（1），（2），（3）可以算出绝热压缩段的马赫数分布，以及芯流面积的分布，再根据气体动力学公式可以算出相应的温度和总压分布。

2.1.2 等压燃烧段（xd～xs）

相对于燃烧室的面积的变化和热附加而言，壁面摩擦、热交换和燃料流量的附加是次要的因素，因此可以忽略。于是，根据一维流动理论的推导，马赫数沿气流的变化可以表示如下

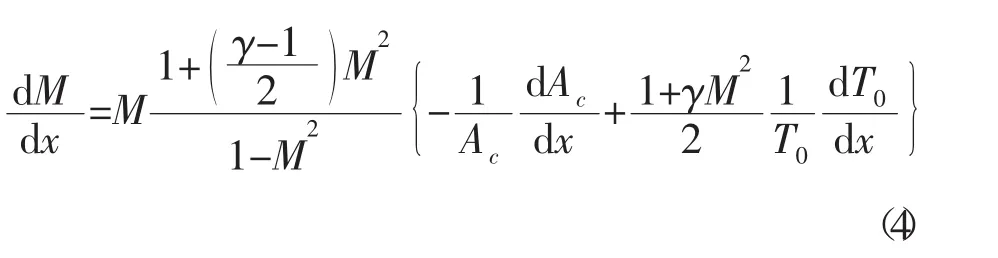
式（4）可以简化为

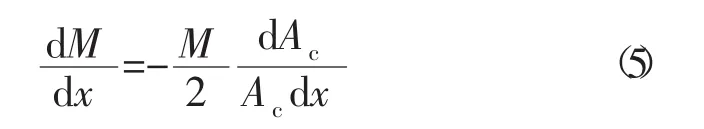
该微分方程（5）中存在芯流面积，所以要解出该方程，必须要先知道芯流面积的表达式。在现有的文献中，芯流面积的公式是在d～s段内用插值方法获得，但是该方法可以利用的插值点也就是两个，即d点和s点，d点芯流面积通过绝热压缩段的计算可以得到，而s点是分离流再附着点，所以该点的芯流面积则是超燃燃烧室的物理面积。由于该插值计算插值点较少，所以插值获得的芯流面积的精度较低，不能较好地反映流场的实质。根据推导可以得到等压燃烧段芯流面积的表达式为

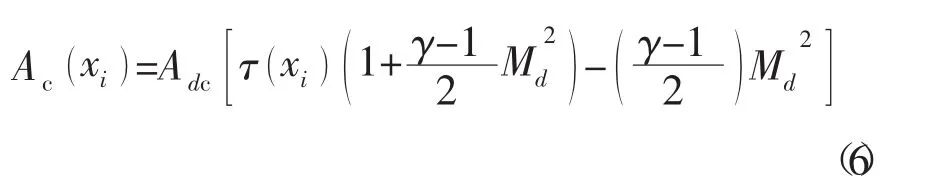
式（6）中τ xi（）为无量纲总温的有理函数，它表示了等压燃烧段中的释热规律。

θ值愈大，释热愈迅速，所以θ反映了释热的快慢。θ为一经验常数，取决于燃料喷射方式和油气混合程度，针对氢燃料，Billig给出了一经验公式：

ER为当量比，在贫油燃烧时小于1。

联立式（6），（7），（8），（9）可以得出芯流面积的计算公式，从而利用四阶Rung-Kutta方法求解式（5），可得到等压燃烧段马赫数分布，进而根据气体动力学公式，可得到温度和总压分布。

2.1.3 非绝热再附着段（xs～x4）

在Crocco一维流动理论的基础上，Billig建议该区域的静压强与燃烧室的横截面面积由多变过程控制，即为公式（10）所示：

其中指数n可以通过公式（11）计算得到：

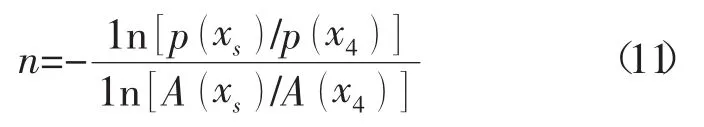
通常可以选取合适的点，使式（10）的理论曲线更靠近试验测得的壁面压强。

2.2 模型二处理过程

模型二是将绝热压缩段2～d和等压燃烧段d～s合并处理，非绝热再附着段s～4单独处理。

2.2.1 合并的绝热压缩和等压燃烧段（x2～xs）

根据一维流动理论，马赫数分布公式为

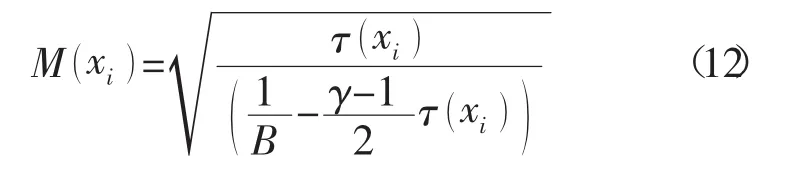
其中，B是I xi（）的函数。

因此，利用式（12）可得到合并的绝热压缩段和等压燃烧段的马赫数的分布，然后利用下式：

可以得到沿程的压强分布，式（13）中的A是指芯流面积，最后根据气体动力学公式可以得到总压和温度的分布。

2.2.2 非绝热再附着段（xs～x4）

在该模型中，非绝热再附着段s～4的处理过程和模型一一致，根据模型一的处理过程，可以得出模型二该段的各个参数。

2.3 一维模型的实际应用

1977 年前后Billig等人做了大量试验，研究了不同类型超燃燃烧室结构，得出了较多的试验数据，以后进行进一步的研究提供了坚实的试验基础。Billig和Grenleski研究的轴对称、壁面喷射的超燃燃烧室模型的组成为：一段长为0.28 m的截面积0.003 8 m2的圆柱，之后紧接着的是长为0.61 m的发散性圆锥。在x=0处沿周向均匀分布8个直径为2.64 mm的氢燃料喷射口。

根据试验报告，超燃燃烧室进口各参数分别为：总温2280 K，总压3.13 MPa，马赫数3.23。Billig在试验过程中获得了轴向静压分布数据。一维模型模型计算出的超燃燃烧室静压与总压之比如图2所示。

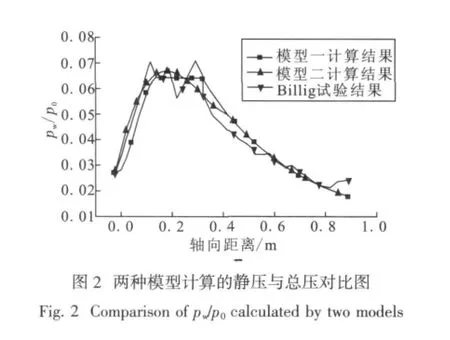
从计算结果可以看出，造成等截面压强上升的原因是隔离段激波链的绝热压缩而不是燃烧释热。燃烧释热从d（图1）点开始，该点由于燃烧室释热产生反压，需要由隔离段绝热压缩引起的压强与之匹配。通常情况下压强上升很快，可以认为d点是隔离段的出口与燃烧室进口的交界面，由于分离流的存在，使得燃烧峰值压强通过在壁面分离流内的传播平均化，在d～s内范围内形成等压释热。气流在s点重新与壁面再附着，从s点至燃烧室出口由于面积扩张起了主导作用，所以压强下降。

两种模型计算出的马赫数如图3所示。两种模型计算出的温度如图4所示。

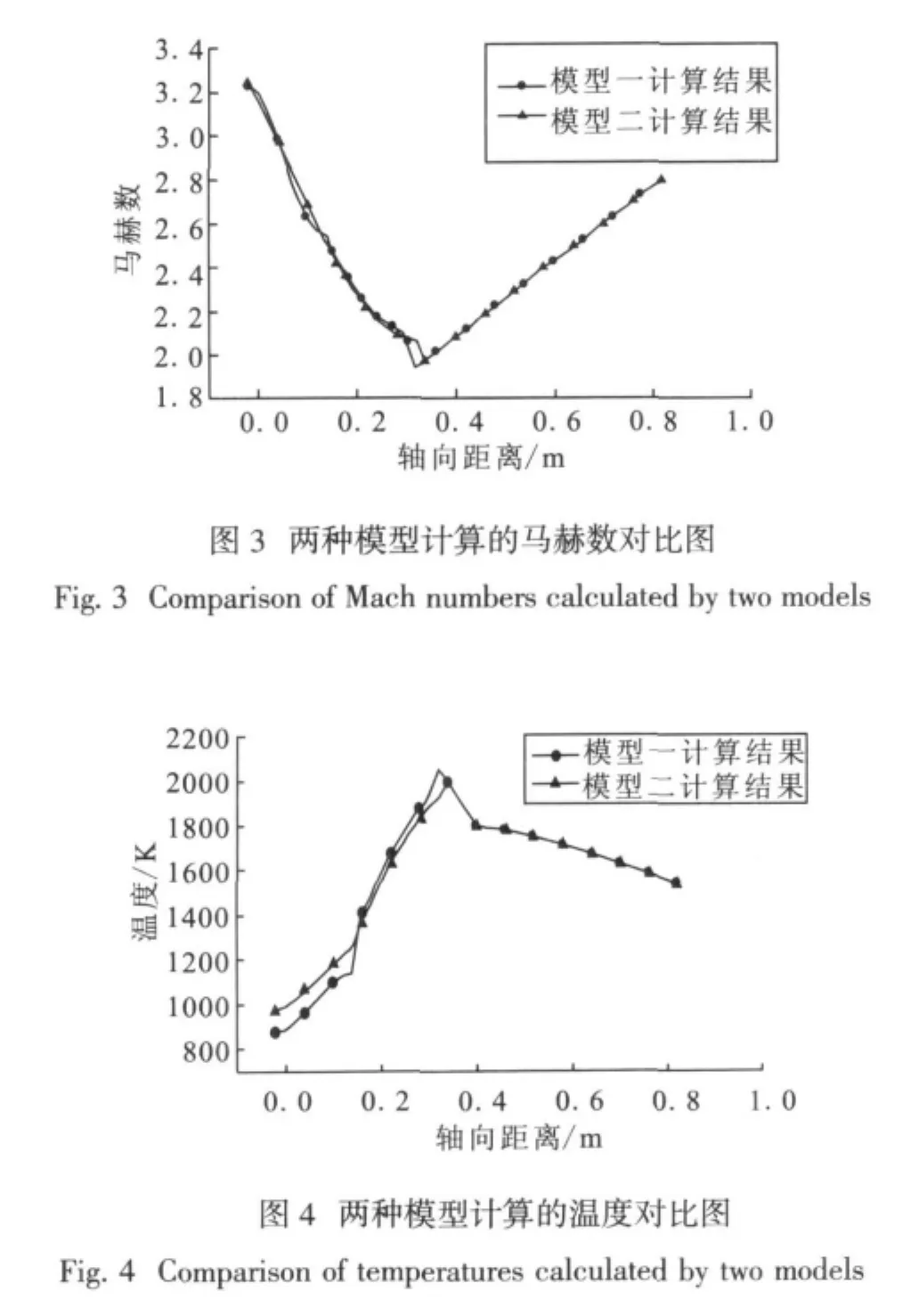
从计算结果可以看出，两种一维分析模型的计算结果与试验数据吻合较好，误差小于5%，可以应用于工程实际。模型一和模型二相比，由于模型一所考虑的过程比较多，各个过程分开进行研究，所得的计算数据与实际情况十分接近，因此模型一为优选一维流动分析模型。

3 超燃燃烧室三维流场的数值模拟

3.1 加长隔离段超燃燃烧室网格的绘制

加长隔离段的超燃燃烧室的组成为：一段长为0.295 m的截面积为0.003 8 m2的圆柱，之后紧接着为0.61 m的发散型圆锥，它的两个底面的面积比为2。

首先利用Gridgen软件把该燃烧室的网格绘制出来。在网格绘制过程中，为了防止计算量太大，超燃燃烧室在周向上只取了1/4来进行研究。离散网格单元数为640 000个，如图5所示。

3.2 加长隔离段超燃燃烧室的边界条件

在加长隔离段超燃燃烧室中，Billig试验时的进口参数为：

当量比Φ=0.63，滞止温度T0=2 295 K，温度T=8.78×102K，压强 p=6.18×104Pa，滞止压强p0=3.14×106Pa，马赫数 M=3.22，K=0.04。

由M=3.22，则根据速度系数公式

可以得到λ=2.01。

根据公式

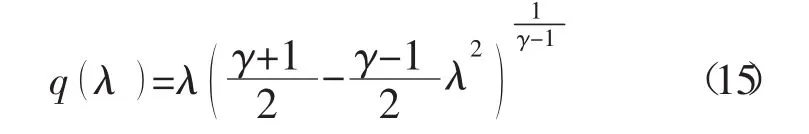
根据一维流动理论，推导出质量流量公式为

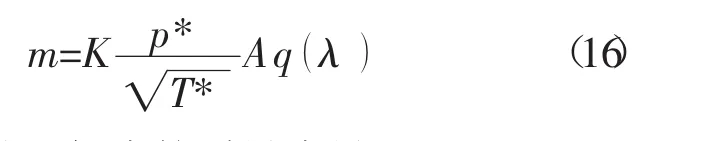
可以得到进口气流的质量流量m=1.93 kg/s。

然而，进入燃烧室中的空气组分文献中没有指定，因此，进入燃烧室的各静态参数的取值范围很广，本文中假定，来流空气的体积组成是氮气78%，氧气21%，氩气1%，这些假定的参数值都落在Billig试验报告的参数范围内，而且更接近报告中进入的质量流量。

试验中氢气参数为：滞止温度T0=643 K，温度 T=555.83 K，马赫数 M=1。根据公式（14），（15），（16）可以计算出氢气的速度系数为 λ=1，q（λ）=1，滞止压强为 p*=1.92×106Pa，压强为p=1.02×106Pa。

在三维数值模拟中，考虑到出口处气流为超声速流动，出口参数由上游参数外推。

3.3 加长隔离段超燃燃烧室三维数值计算

在加长隔离段超燃燃烧室三维数值模拟中，使用FLUENT三维处理软件，采用的分析方法是：

1）数值计算方法采用的是有限体积法；

2）求解方法采用隐式化的数值求解法；

3）粘性系数采用萨特兰公式；

4）计算理论采用流体动力学理论；

5）燃烧模型采用有限速率涡扩散模型；

6）化学反应采用2H2+O2=2H2O一步反应方程式。

为了提高计算效率，本文进行了并行计算，得出了三维数值模拟结果。

从图6中可以看出，三维模拟的壁面静压数据与试验数据十分吻合，特别是在后一段，几乎贴近试验数据点，误差小于2%。因为本文三维数值模拟只简化采用了一步化学反应模型，即2H2+O2=2H2O，而在实际的超燃燃烧室中，中间化学反应过程达到了几百个，而且还有几百种中间气体组分的相互作用，所以前一段与试验数据不是十分接近，这也说明了超燃燃烧室流场的复杂性。

中心线处马赫数的计算结果如图7所示。从图7中可以看出，马赫数在压缩段和燃烧段的总的趋势是降低的，而在膨胀段则是升高的，与实际情况相吻合。而且在x=0的喷口左右，由于此时喷入氢燃料燃烧，所以马赫数下降较快。在超燃燃烧室膨胀段中马赫数是波浪式地升高的，接近于实际情况。

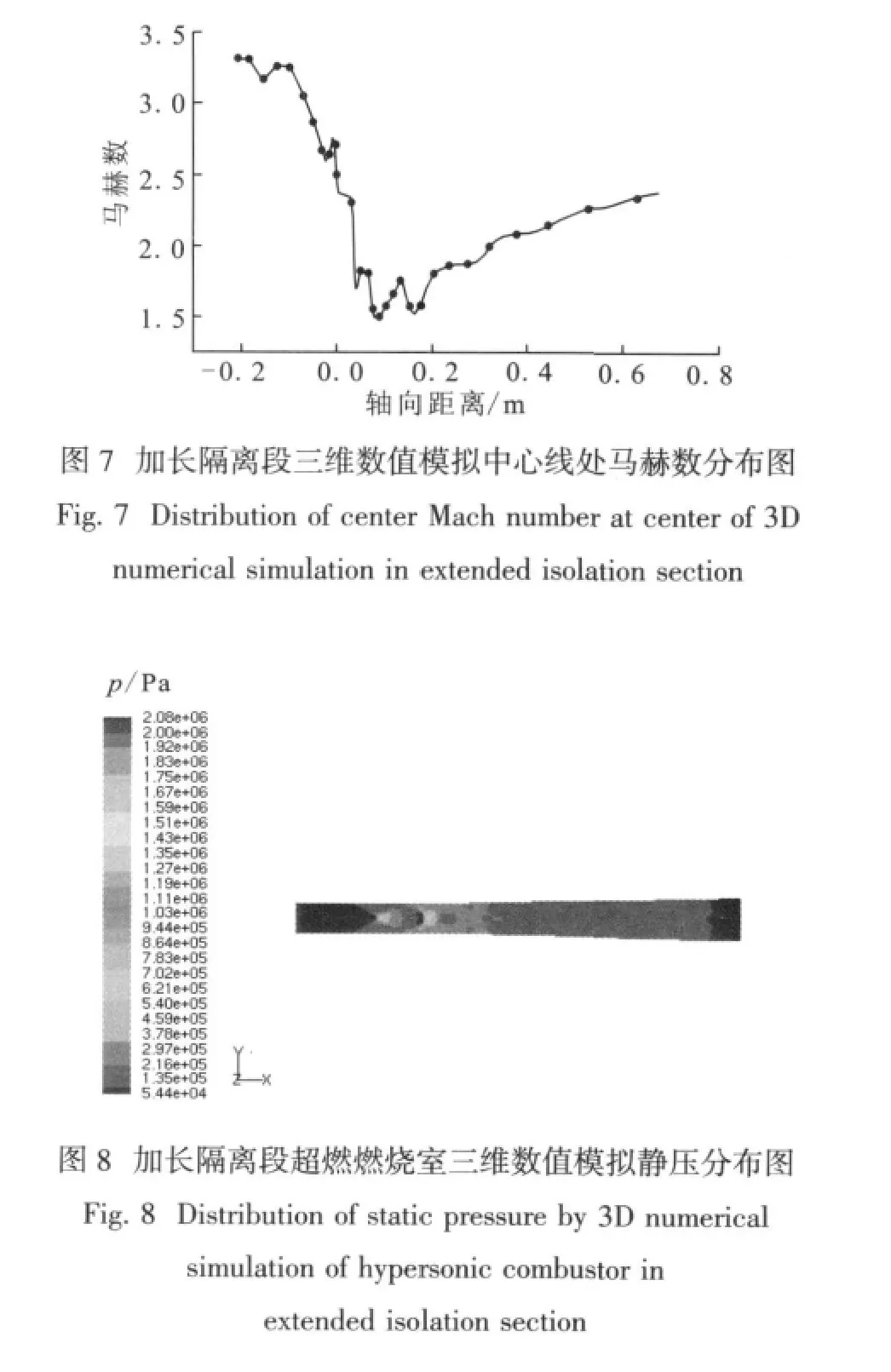
加长隔离段流场的静压分布如图8所示。从图8中可以看出，刚开始时来流气流的压强较低，进入燃烧室时，在斜激波串的作用下，压强开始逐渐升高，然后经过燃烧段时，压强开始波浪起伏，最后在膨胀释热段压强开始逐渐下降，而且可以方便看出压强在同一截面处的变化。

加长隔离段流场的马赫数分布如图9所示。从图9中可以看出，来流马赫数在斜激波的作用逐渐降低，在氢燃料喷口后x=0.1 m处，马赫数降至最低，最后在膨胀释热段，马赫数开始回升，而且在同一截面处，马赫数在壁面处最小，向中心靠近，马赫数逐渐增大。

加长隔离段流场的温度分布如图10所示。从图10中可以明显看出，温度在斜激波串的作用下升高，而且在燃烧段时温度也逐渐增大，然而在膨胀释热段温度开始下降，与实际情况一致。壁面处的温度比同一截面其它地方要高。

从计算结果可以看出氢燃料在喷口处M=1的速度喷出，然而逐渐向壁面扩散。根据计算结果，燃烧掉的氢气占氢气总量的80%。

从以上的三维流场的分析可以知道，超燃燃烧室的流动现象十分复杂，充满了不稳定的激波系、膨胀波系。特别是进气道、隔离段产生的厚边界层和分离流与燃烧室中众多的燃料射流以及漩涡结构的相互作用更是增加了流场的复杂程度。对于氢燃料来说，需要考虑几百个中间反应过程和几百种中间气体组分的相互作用，即使模型简化后的数值模拟也存在计算量太大的问题，本文对三维数值模拟进行了一步反应分析，揭示出了超燃燃烧室中一些复杂的流动现象。

4 结论

本文在分析超燃燃烧室内流场特性的基础上，研究了超燃燃烧室一维流动分析模型，主要结论有：

1）一维模型分析中芯流面积的确定十分关键，本文通过比较分析了国内外关于一维流动分析芯流面积确定方法的文献资料，获得了芯流面积的计算公式；

2）将一维流动模型应用到实际的超燃燃烧室的计算上，并且与试验数据进行了对比，误差小于5%，验证了一维模型的有效性，同时确定出最优一维分析模型。

由于一维模型仅能模拟轴向的一维参数变化规律，不能充分详细反映超燃燃烧室截面上的参数分布，而且二维计算中燃料的喷注不能得到完全真实的模拟，因此为了能更为详细地获得流场各个参数，本文还进行了三维数值模拟，主要结论有：

1）三维数值模拟能较好的反应超燃燃烧室的全貌，并且与试验结果很接近；

2）由于简化采用了一步化学反应模型，所以导致燃烧段计算结果与试验数据差距较大，但非绝热再附着段计算结果与试验数据很接近，误差小于2%，因此在后续研究中可考虑多步化学反应。

超燃冲压发动机燃烧室流场十分复杂，本文研究的内容还不够深入，因此有必要在今后的研究中进一步完善，主要包括：

1）建立高精度、高效率求解三维定常/非定常全NS方程的应用程序；

2）发展用于反应流的多重网格方法，以提高收敛速度；

（3）完善用于高速流动反应流的湍流模型，来模拟湍流流场和正确的耦合湍流对化学反应及化学反应对湍流的影响；

（4）通过对超燃燃烧室的分析来系统地减少化学动力学模型中的反应式的个数，从而降低对计算机的要求。

[1]张蒙正,张忠利,葛李虎，仲伟聪.一体化超燃冲压发动机初步设计计算模型[J].火箭推进,2005,31(1):16-22.

[2]HEISER W H,PRATT D T,DELEY D H.Hypersonic airbreathing propulsion[M].Washington,DC:AIAA,1994:334-370.

[3]YU G,LI J G,ZHAO J R,et al.Experimental studies on H2/air model scramjet combustor,AIAA 99-2449[R].US:AIAA,1999.

[4]西工大、南航、北航三校合编.气体动力学基础[M].北京:国防工业出版社,1980.

[5]A H夏皮罗（美）.可压缩流的动力学与热力学[M].陈立子译.北京:科学出版社,1966.

[6]李大鹏.煤油双模态冲压燃烧室工作过程研究 [D].长沙:国防科学技术大学,2006.

[7]张鹏,俞刚.超燃燃烧室一维流场分析模型的研究[J].流体力学实验与测量,2003,17(1):88-92.

[8]OBRIEN Timothy F,STARKEY Ryan P,LEWIS M J.Quasi-one-dimensional high-speed engine model with finite-rate chemistry[J].Journal of Propulsion and Power,2001,17(6):1366-1374.