频谱分析中的微分法与微分方程法

薄 华，任 蕾，陈红亮，金欣磊，杨忠根

(上海海事大学电子工程系，上海200135)

正如许多“信号与系统”教材［1-5]指出的那样，用微分法可计算非周期信号f(t)的傅里叶变换(FT)。其过程是，首先可根据FT的微分性质得出f'(t)=g(t)的FT:jωF(jω)=G(jω)，由它得出f(t)的FT:F(jω)=G(jω)/(jω)。实际上，如果不注意上述过程中隐含的假设而直接引用，有时会给出错误的结果。

例如，让我们看一下用FT的微分性质求解三个典型信号u(t)、u(-t)和sgn(t)的FT的结果，如

表1所示。表中也示出了正确结果用作比较。

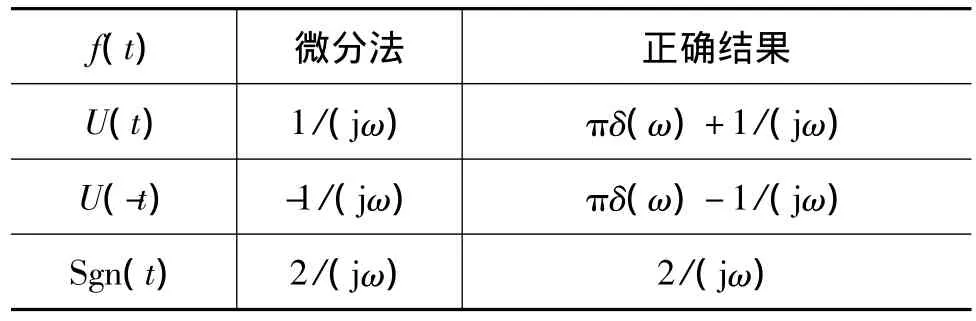
表1 用FT的微分性质求解FT的结果

从表1可见，此法给出了一次正确计算结果和两次错误计算结果。我们不禁要问，为什么会给出这样的计算结果?能否对它进行必要的修正来给出正确的计算结果?究竟在哪些场合能使用微分法?什么时候不需要修正?什么时候需要怎样的修正?这些就是本文首先要回答的问题。

1 微积分性质的隐含假设及其修正

为了拓广其用于计算含有非零直流分量的信号的FT，我们仅需在得到jωF(jω)=G(jω)之后改由F(jω)=+G(jω)/(jω)给出f(t)的FT即可。这就是修正微分法。

值得注意的是，文献［3] 在指出FT的积分性质隐含的假设后，便给出了用修正积分法计算f(t)的公式:F(jω)=此公式与这儿的修正微分法给出的公式一致，因为=f(-∞)+0.5G(0)。

表2给出了微分法和修正微分法求解FT的结果，与表1给出的正确结果比较后可见，与微分法仅对的信号能给出正确的结果不同，修正微分法能对所有情况都给出正确的结果。

2 微分方程法与生成系统模型

本节对修正微分法进行推广。有许多信号可表示为微分方程的输出。这就是频谱分析中的微分方程法。实现该微分方程的系统就是信号的生成系统。需要指出的是，随机信号功率谱分析中使用的生成系统模型法是这儿的生成系统模型法的推广。此处用单位功率的白噪声取代这儿的冲激信号来激励生成系统。

2.1 不含正弦分量时的微分方程法

［例1] 因果指数衰减信号e－αtu(t)，α＞0

对该信号求导后，易知它满足微分方程f'(t)+αf(t)=e(t)，其中输入e(t)=δ(t)。因此，它的FT就是此微分方程对应的系统的频率传递函数F(jω)=H(jω)=1/(α+jω)，此系统可视为该信号的生成系统。在此例中，珓f=0，而且信号不含正弦分量，故无需进行修正。

［例2] 双边指数衰减信号e－α|t|，α＞0

对它求二阶导数并利用|t|'=sgn(t)后，易知它满足微分方程f″(t)+α2f(t)=2αe(t)，其中输入信号e(t)=δ(t)。因此，它的FT就是此微分方程对应的系统的频率传递函数F(jω)=H(jω)=2α/(α2－ω2)，此系统可视为该信号的生成系统。在此例中，而且信号不含正弦分量，故也无需修正。

2.2 含正弦分量时的微分方程法

［例3] 因果复正弦信号ejω0tu(t)

对该信号求导后，易知它满足微分方程f'(t)－jω0f(t)=e(t)，其中输入e(t)=δ(t)。因此，它的FT就是此微分方程对应的系统的频率传递函数。在此例中，故无需进行因直流分量引起的修正。但信号里含正弦分量，由于(ω－ω0)在算子j(ω－ω0)的零空间中，故需进行因正弦分量引起的修正。与前述的修正微分法相似，首先计算因果复正弦信号含有的复正弦分量kejω0t，其中:

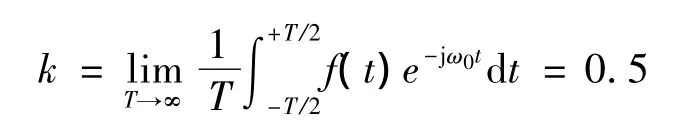
然后，利用复正弦信号ejω0t的FT对系统传递函数进行修正得到:F(jω)=H(jω)=δ(ω－ω0)+1/［j(ω－ω0)] 。此修正从本质上解释了当信号的拉普拉斯变换LT含有虚轴上的极点时，从LT求解FT需进行修正的原因。

［例4] 复正弦信号ejω0t

对它求导之后满足微分方程f'(t)=-jω0f(t)=0，对它进行FT，有j(ω－ω0)F(jω)=0，此时k=1，所以F(jω)=2πδ(ω－ω0)。此分析过程表明，复正弦信号生成系统是个无输入的自激振荡器。

2.3 用于FIR信号的微分方程法

由于FIR信号既不含直流分量，也不含任何正弦分量，因此，可无需任何修正地使用微分性质和微分方程法。

［例6] 梯形脉冲信号r(t+3)－r(t+1)－r(t－1)+(t－3)。

对它求二阶导数后，易知它的生成系统微分方程f″(t)=e(t+3)－e(t+1)－e(t－1)+e(t－3)是它的微分方程，其中输入e(t)=δ(t)。因此，它的FT就是此微分方程对应的系统的频率传递函数:F(jω)=H(jω)=(4/ω2)sinωsin2ω。

3 结语

从本文的讨论可以看出，FT的微分性质隐含地假设了信号不含有直流分量，这使得它的应用范围受到限制。为解决此问题，我们对它进行了简单有效的修正，使它能在不满足隐含假设的场合给出正确的结果。然后，我们推导了作为信号生成系统的微分方程描述，使信号谱成为其生成系统的频率传递函数;同时指出微分方程法也隐含地假设了信号不含直流分量和正弦分量，并给出了当信号违反此假设时进行修正的方法。此修正方法从本质上解释了当信号的拉普拉斯变换LT含有虚轴上的极点时，从LT求解FT需进行修正的原因。

［1] 郑君里，应启珩，杨为理.信号与系统(第二版)［M] .北京:高等教育出版社，2000年

［2] 管致中，夏恭恪，孟桥.信号与线性系统(上册)(第4版)［M] .北京:高等教育出版社，2004年1月

［3] 吴大正主编，杨林耀，张永瑞编.信号与系统(第三版)［M] .北京:高等教育出版社，1998年

［4] 刘树棠译，A.V.Oppenheim，A.S.Willsky，W.S.H.Nawab著.信号与系统(第二版)［M] .西安:西安交通大学出版社，1998年

［5] 杨忠根，任蕾，陈红亮.信号与系统［M] .北京:电子工业出版社，2009年6月出版