电压空间矢量PWM控制技术的探讨

赵 利

(山西大同大学电气工程系，山西大同037003)

电压空间矢量PWM，SVPWM(Space Vector PWM)控制技术是电力电子电路采用的重要控制技术之一，也是在实践应用中性能较好一种控制技术，掌握它对学习交流电动机调速系统知识具有重要意义。在有关SVPWM控制技术的文献中，由于一些关键性问题没有讲清楚，使我们无法准确全面地理解SVPWM控制技术。本文就这些关键性问题进行深入剖析。

1 问题的提出

对于基本的电压型逆变器，采用180o导通方式，如图1所示。如对三相开关的导通情况进行组合，共有八种工作状态。其中六种状态输出六个有效电压矢量u1～u6，两种状态输出两个零电压矢量u0和

在一个周期T1内，六个有效工作矢量顺序各作用一次，形成一个封闭的正六边形旋转磁场［2]，如图2所示。

对于三相异步电动机，忽略定子绕组电阻和漏磁感抗压降后，可认为定子相电压U1=Eg，即［3]

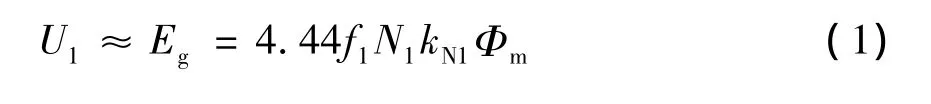
图2 正六边形定子磁链旋转磁场

我们知道，在基频以下调速时，气隙磁通Φm是恒定不变的［4]，即Eg/f1=常数。

现在的问题是对于基频以下调速，当频率f1降低时，电动机定子相电压U1亦降低。然而U1/f1值为何保持不变呢?下面就这一问题进行探讨。

2 基本电压矢量产生的SVPWM波

一般在实现SVPWM控制方法时，为了减少谐波分量，尽可能使PWM波形对称，在每相邻两个基本电压矢量之间依次插入零电压矢量u7和u0，得到的SVPWM波如图3所示。

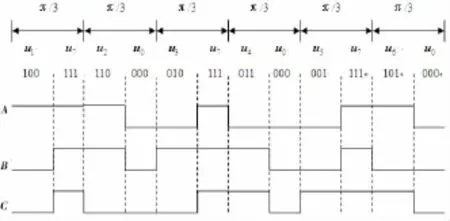
图3 零电压矢量和基本电压矢量共同实现SVPWM波

从图3可看出，A、B、C三相PWM电压波的基波成分大小相等、频率相同且相位相差2π/3电角度。将A相波形置于如图4所示坐标系中，结合图3容易知道图4中各点α1，α2，α3和α4的值，他们分别为α1=/3+ω1·Δt1，α2=/3+ω1·Δt1，α3=/3+ω1·Δt及α4=3+ω1·Δt1。

这里，为逆变器提供电源频率ω1==，每个有效电压矢量作用的时间为Δt1。

图4 A相电压的SVPWM波

式中，

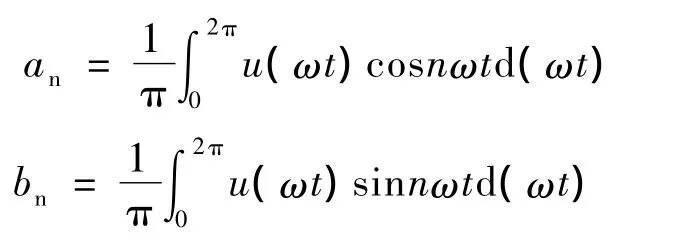
其基波分量a1和b1的值为

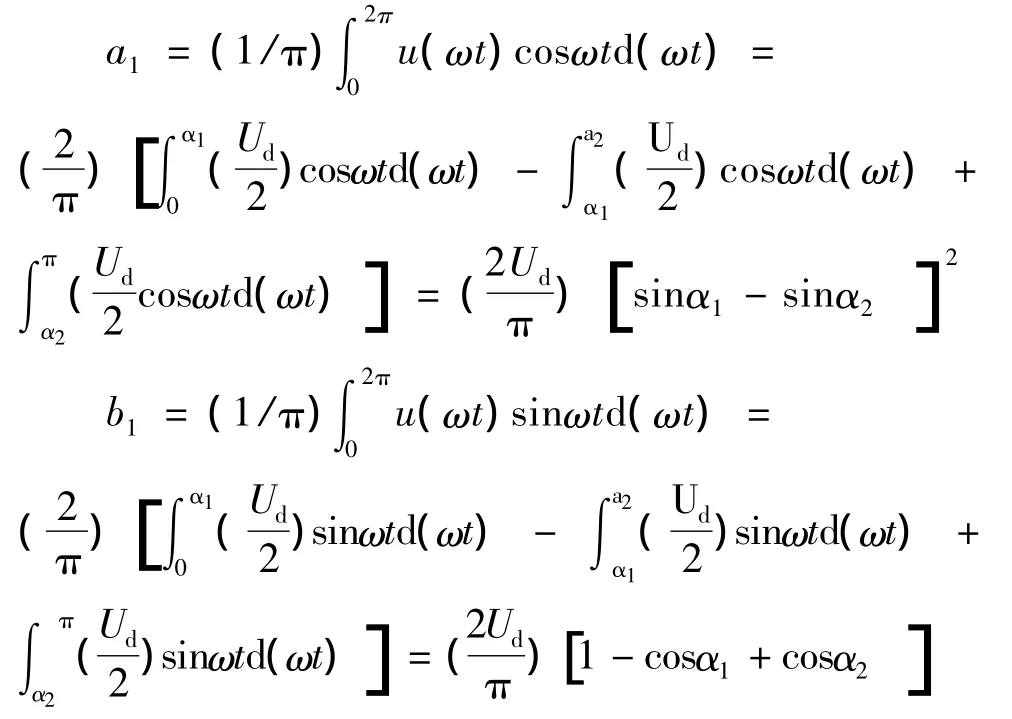
基波电压的幅值U1m为

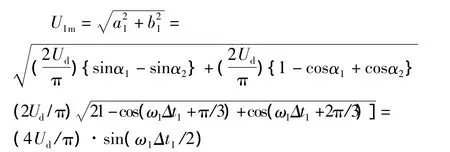
基波电压幅值与频率比为

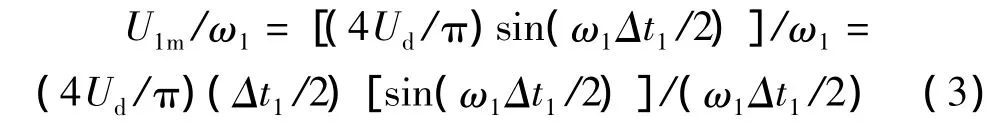
式中，ω1Δt1和ω1Δt0分别是一个有效电压矢量和一个零电压矢量在一个扇区/3弧度内作用产生的角度，即ω1Δt1+ω1Δt0=/3。当ω1Δt1＜(1/3)(/3)=/9，即ω1Δt1/2＜(/18)，下式近似成立:

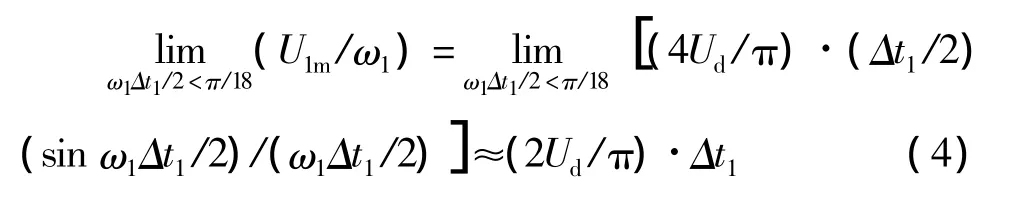
在此之所以作这样近似处理是根据实际情况出发，即SVPWM控制产生的都为多边形旋转磁场。如24边形旋转磁场，这样每个有效电压矢量作用的最大角度为ω1Δt1=2/24=/12，从而ω1Δt1/2=/24，则上式(4)更加精确。即U1m/ω1值逼近常数(2Ud/)·Δt1这里的Δt1，实际上是常数［2]。

可见，在基频以下调速时电压频率比近似为恒值，即与ω1无关。

3 结语

本文利用SVPWM控制技术产生的正六边形旋转磁场，在六个有效电压之间插入零电压矢量。我们利用得到的SVPWM波及傅立叶级数基本知识，可以证明基频以下调速时采用SVPWM控制技术逆变器输出电压频率比为恒值。这对准确而全面理解SVPWM控制技术，深刻掌握交流调速系统有关内容具有重要意义。

此外，要特别强调以下两方面问题。

(1)采用SVPWM控制技术的逆变器输出是PWM电压波，即交流电动机得到的是PWM波。所以上述提到的U1应该是指PWM波中基波成分的有效值(或幅值U1m=

(2)采用正六边形旋转磁场，目的是为了使证明变得简单。可以想象，对多边形旋转磁场结论亦成立，但会使证明复杂，同时结果更为精确。

［1] 王兆安，刘进军.电力电子技术(第5版)［M] .北京:机械工业出版社，2009

［2] 阮毅，陈伯时.电力拖动自动控制系统(第4版)［M] .北京:机械工业出版社，2010

［3] 李发海，王岩.电机与拖动基础(第3版)［M] .北京:清华大学出版社，2003

［4] 李华德.交流调速控制系统［M] .北京:电子工业出版社，2007