关于互易二端口网络互连的讨论
田社平,陈洪亮,张 峰
(上海交通大学电子信息学院,上海200240)
互易电路是一类较为特殊的电路,它是电路课程教学中较为重要的教学内容之一。互易二端口电路是互易电路的典型形式,其性质可由互易定理加以描述。二端口电路的互连亦是电路课程教学的重要内容。如果将互易二端口电路互连,互连后得到的二端口电路是否仍然满足互易性?如果要满足互易性则需设定什么条件?互易二端口电路的互连有何应用?这些都是笔者在教学过程中碰到的问题。
1 互易二端口电路的判定规则
二端口电路的参数矩阵元素间的关系可以用来判定一个二端口电路是否为互易二端口电路。如果已知二端口电路的开路电阻矩阵R,或电路电导矩阵G,或混合参数矩阵H和,或传输参数矩阵A和,则当二端口参数矩阵元素满足如下关系时,该二端口电路为互易二端口电路[1]:

2 互易二端口电路互连的互易性
常见的二端口互连形式包括串联、并联、串-并联、并-联和级联等。如果互连的二端口电路是互易的,则在各种互连形式下得到的总二端口电路的互易性具有下述结论:对互易二端口电路N1和N2,如果互连(串联、并联串-并联、并-串联和级联)后N1和N2仍然满足端口定义,则互连得到的总二端口电路也是互易的。以下分别予以证明。
(1)串联和并联
假设N1和N2的r参数矩阵分别为

串联后总二端口电路r参数矩阵为R。由于串联后N1和N2仍然满足端口定义,因此有[2]

因N1和N2是互易的,由式(1)可得r21=r12,r'21=r'12,因此有

即R为对称矩阵,因此串联后总二端口电路是互易的。
同理,可证互易二端口电路N1和N2并联后总二端口电路也是互易的。
(2)串-并联和并-串联
假设N1和N2的h参数矩阵分别为

串-并联后总二端口电路h参数矩阵为H。由于串-并联后的N1和N2仍然满足端口定义,因此有[2]
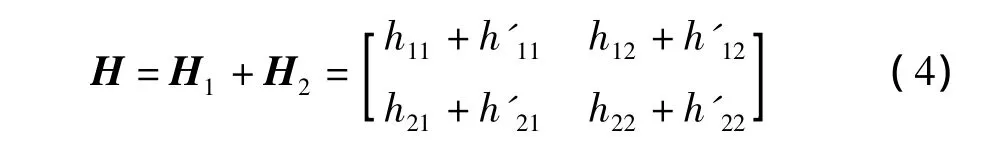
因N1和N2是互易的,由式(1)可得,h21=-h12,h'21=-h'12,因此有

即H为对称矩阵,因此,串-并联后总二端口电路是互易的。
同理,可证互易二端口电路N1和N2并-串联后总二端口电路也是互易的。
(3)级联电路。
假设N1和N2的a参数矩阵分别为

级联后总二端口电路a参数矩阵为A。由于级联后N1和N2总是满足端口定义,因此有[2]

从而得到

因N1和N2是互易的,由式(1)可得a11a22-a12a21=1,a'11a'22-a'12a'21=1,由该两式及式(7)可得由式(1)可知,级联后总二端口电路是互易的。由上述证明过程可知,对多个互易二端口电路的互连,上述结论仍然成立。

[例1]试判断图1所示电路是否为互易二端口电路。

图1 级联二端口电路
解:将图1电路看作两个二端口电路(从虚线处断开)的级联,由于虚线右边电路仅由电阻构成,因此该二端口电路为互易电路。虚线左边二端口电路的r参数矩阵满足互易条件,因此图1电路为互易的。
我们也可通过求出图1电路的参数矩阵进行判断,但过程会复杂一些。
3 互易二端口电路互连的有效性判断
二端口电路在串联、并联和串-并联和并-串联时存在有效连接(二端口电路互连后仍满足端口定义)的问题[3]。如果要求互易二端口互连后总二端口电路仍然是互易的,则须保证互连是有效连接。如果互连不是有效连接,则可采用变压器隔离法来实现有效连接,图2给出了并联二端口电路的变压器隔离方法。
值得指出的是,变压器可连接在二端口电路N1和N2的输入、输出端口的任一端口。对串联和串-并联和并-串联二端口电路的变压器隔离方法,可给出类似结果。
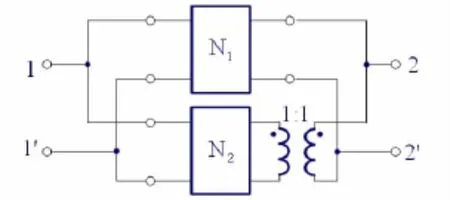
图2 并联二端口电路的变压器隔离
4 对称二端口电路的互连
如果互易二端口电路的两个端口可以交换而端口的电压和电流的数值不变,则称该二端口电路是对称的。对称二端口电路的参数矩阵的元素除满足式(1)之外,还满足如下关系:

采取类似的推导方法,我们可以得到如下结论:对两个对称二端口电路N1和N2,如果互连(串联、并联和串-并联、并-串联、级联)后N1和N2仍然满足端口定义,则互连得到的总二端口电路也是对称的。
5 结语
本文针对互易二端口电路互连的互易性进行了讨论,并给出了一般性结论。尽管电路的互易性不具有普遍性,互易电路的性质(互易定理)的应用面也较窄,但笔者认为,通过对电路包括二端口电路互连的互易性进行深入讨论,有助于加深学生对互易电路及二端口电路互连等概念的理解。本文的讨论拓宽了电路教材中关于互易电路及二端口电路互连的教学内容,有助于电路课程的教学,可供从事电路教学的教师参考。
[1] 李瀚荪.简明电路分析基础[M] .北京:高等教育出版社.2002
[2] 陈洪亮,张峰,田社平.电路基础[M] .北京:高等教育出版社.2007
[3] 田社平,张峰,陈洪亮.双口网络有效互连的判据和实现[J] .南京:电气电子教学学报,2005(5)

