感受数学文化 提高数学素质

张艺萍，孟冬梅，刘海涛

（天津市新华职工大学，天津市 300040）

感受数学文化 提高数学素质

张艺萍，孟冬梅，刘海涛

（天津市新华职工大学，天津市 300040）

数学是人类科学发展的重要工具，然而对数学的学习却成为成人高校学生的头疼之事，传统的教育模式造成教师难教、学生难学、学习的收获微小等问题。因此，成人高校的数学教育工作成为我们成人教育工作者应该研究的课题。文本探讨了在成人高校的数学教育中引入数学文化知识，紧密结合实际应用问题讲授数学课、传授数学文化、提高学生的数学素质的必要性与可行性。

数学课程；成人教育；数学文化；数学素质

一、数学文化及其在成人教育中应起的作用

著名数学家华罗庚教授说：“宇宙之大、粒子之微、火箭之速、化工之巧、地球之变、生物之谜、日用之繁，数学无处不在”．概括了数学学科在人类发展中的重要作用．

提起数学，童叟皆知．而“数学文化”一词是否为人们所了解呢？“数学文化”并非指单纯的数学知识，而是指数学知识的积淀．它包括：数学的思想、精神、方法、观点、语言，以及它们的形成和发展．除上述内涵以外，还包含数学家、数学史、数学美、数学教育、数学发展中的人文成分、数学与各种文化的关系．

一位数学教育家说，不管人们从事什么工作，深深铭刻在头脑中的数学的思想精神、数学的思维方法和看问题的着眼点等，都会随时随地发生作用，使人们终生受益．

我们从事的是成人大专教育，我们教学的对像是成人大专的学生，他们大都是工作一线的实际应用人才，在实际工作中很少直接应用到数学知识，而通过学习数学所得到的“数学素质”，却能够让他们在工作和生活中发挥作用．这包括1．熟练地用准确、简明、规范的数学语言表达自己数学思想；2．具有良好的科学态度和创新精神，合理地提出新思想、新概念、新方法；3．对各种问题以“数学方式”的理性思维，从多角度探寻解决问题的方法；4．善于对现实世界中的现象和过程进行合理的简化和量化，并以数学的方法解决等方面．

二、在成人院校进行数学文化推广的可行性

现在有一些高校给大学生开设数学文化课，并不以传授数学理论知识为主要目的，而是以教授数学思想、提升学生的数学素养为主，同时也提升学生的文化素养和思想素养．内容大致包括：关于数学的概述；若干数学问题中的数学文化；若干数学典故中的数学文化；若干数学观点中的数学文化等．

我们成人教育可以此借鉴，在讲授必要的数学知识的同时，结合专业知识，将数学文化融入到教学中，提升学生对数学知识的兴趣，感受到数学的美妙，还可通过现代计算机技术将问题形象化，形象、深刻地理解数学的思想、精髓．再增加一些数学史、数学家的介绍、数学小故事等，调动学生的学习兴趣．

三、数学文化在成人教育的应用举例

1．数学中有一个特殊的数——欧拉数e

欧拉（Euler，L．1707－1783）是瑞士的著名数学家，他有超人的天赋，聪明过人，再加上勤奋好学，一生潜心于数学的研究，在数学上取得了很多重要的研究成果．欧拉数是数学家欧拉首先发现的，因此以他的名字命名称为欧拉数，并以他自己的姓名的字头小写字母e表示，记为e＝2．71828……．欧拉数e是一个无限不循环小数，因此e是一个无理数．

欧拉数可用繁分数来表示：

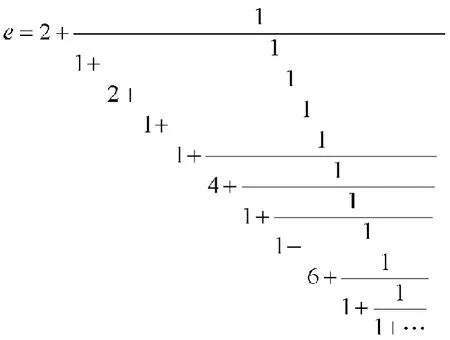
或表示为

欧拉数e也可用无穷级数表示：

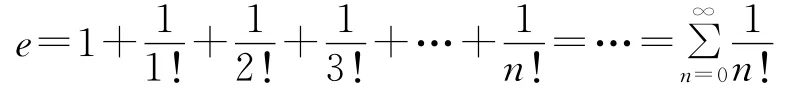
欧拉数e的这几种表达式足以让我们欣赏到数学表示的形式美．

不论用任何一种表达式计算，根据需要可计算出精确到小数点后的任何值．比如保留小数点后十二位的值，e≈2．718281828459．

连续复利问题：设储蓄本金为P，年利率为r定期1年，每年自动转存．第年末的本利和应为Sn＝P（1＋r）n．

若假设计息期无限缩短，则此时t→∞，就会有

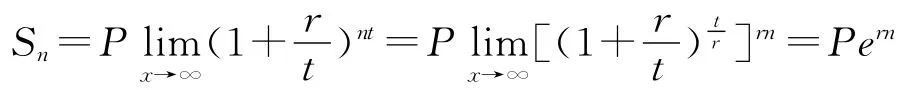
连续复利问题是经济应用中的常见、易懂的问题，在这类问题中引入数学文化知识，更能使学生感兴趣．

2．黄金分割0．618

关于黄金分割〔Golden Section〕的起源大多认为来自毕达哥拉斯．据说在古希腊，有一天毕达哥拉斯走在街上，在经过铁匠铺前他听到铁匠打铁的声音非常好听，于是驻足倾听．他发现铁匠打铁节奏很有规律，这个声音的比列被毕达哥拉斯用数理的方式表达出来，被应用在很多领域．后来很多人专门研究过这一比例，开普勒称其为“神圣分割”．黄金分割在文艺复兴前后，经过阿拉伯人传入欧洲，受到了欧洲人的欢迎，他们称之为“金法”．17世纪欧洲的一位数学家，甚至称它为“各种算法中最可宝贵的算法”．

黄金分割也是一种数学上的比例关系：把长度为1的线段分割成两段，设大的一段为x，小段则为从而得到方程x2＋x－1＝0，其解的正根x＝这样的分割成为黄金分割．

黄金分割具有严格的比例性、艺术性、和谐性，蕴藏着丰富的美学价值．黄金分割的这种比例，给人一种恰到好处的和谐视觉．古埃及的金字塔、古希腊雅典的巴特农神庙、法国埃菲尔铁塔、巴黎圣母院、印度泰姬陵、中国故宫，这些风格各异的世界著名建筑都在构图布局设计上运用了黄金分割的法则，给人以整体上的和谐美，令人赏心悦目．舞台上的报幕员并不是站在舞台的正中央，而是偏在台上一侧，以站在舞台长度的黄金分割点的位置最美观，声音传播的最好．艺术家们认为弦乐器的琴马放在琴弦的0．618处，能使琴声更加柔和甜美．

中科院院士、世界数学大师华罗庚先生是世界著名的数学家，他在解析数论、矩阵几何学、典型群、自守函数论、多个复变量函数论、偏微分方程等很多领域都作出了卓越的贡献．他于六十年代创造的“0．618法”，在化工、军事、农业、工业等行业得到广泛的应用，对我国的经济建设做出了重要的贡献．

“0．618法”是一种求最优化问题的方法，对某类单因素的用最少的试验次数找到最佳试验点问题，在优选法中要优于二分法等其它优选法．

具体方法例如：在炼钢时需要加入某种化学元素来增加钢材的强度，假设已知在每吨钢中需加某化学元素的量在1000克到2000克之间，为了求得最恰当的加入量，需要在1000克与2000克这个区间中进行试验．

做法是：先找到［1000，2000］的0．618分点及0．382分点，即1．382及1．618分别进行试验，对比试验结果。如果1．618的试验结果较好，就去掉［1000，1．382］的一段区间，在［1．382，2000］区间内，再次选该区间的0．618分位及0．382分位重复试验，以此类推，直到找到最佳试验点．

而通常用的“对分法”，是将分点取在区间二分之一处．实践证明，对于一个因素的问题，用“0．618法”做16次试验就可以完成“对分法”做2500次试验所达到的效果．

我在课堂教学中，将这些知识介绍给学生，既能使学生对这一数学文化知识感兴趣，又可以提升他们的数学素质，达到教学目的．还可以让他们将这一优秀的方法带到实践中去，为经济建设做贡献．

3．微积分与几何的和谐统一

在数学中，一维的变量可以被表示在数轴上，二维的变量可以被表示在平面直角坐标系上，三维的变量可以被表示在空间直角坐标系上．

微积分中的一元函数，是两个变量之间的某种关系．一元函数的几何表示为平面上的曲线，变量之间的关联，可以在曲线图中得以淋漓尽致的精确表现．这也是数学的奇异美、和谐美与统一美，是数学文化完美的视觉体现．

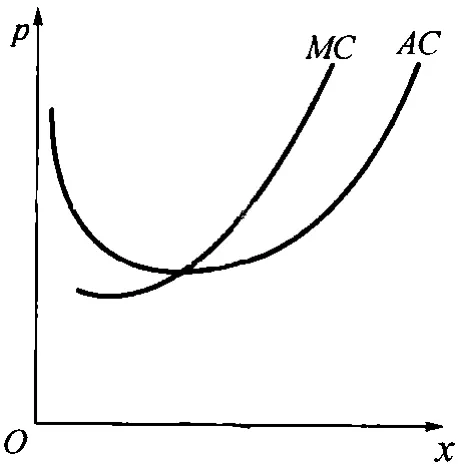
在经济数学中有这样一个问题：设某商品当产量为x时的成本为C（x），平均成本AC＝C（x），边际x成本MC＝C′（x）．从曲线图形上看：当平均成本与边际成本相等时，平均成本取得最小值（如下图）．

我们用课堂中学习的一元函数微分学，也可得到同样的结论．具体推导如下：

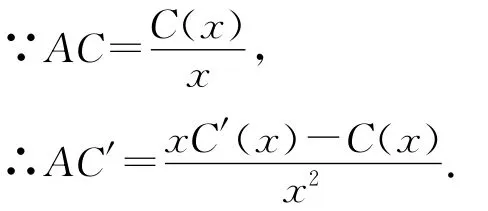
即MC＝AC．

曲线是函数的几何表示，它表征了函数的特性．而微积分的解法，又是问题以高一层次数学思想的解，它不需要做出函数的图形就能够得出相同的结论．

将抽象的数学概念进行几何形式的展现，可以让学生直观地认识到数学的性质，更好的理解和掌握数学知识，降低学习难度，达到提升学生数学素质的目的．

四、小结

社会在不断的发展，人类在不断的进步．作为学生课堂知识的传授者，教师应根据教学对象的现实情况与实际需求，不断学习、更新知识，提高自身的业务水平，与时俱进．

在成人教育教学中引入将数学文化知识，可以使学生对数学及其它课程的学习都产生兴趣．如果他们能以此为启发，在实际工作和学习中，能主动发现并探讨数学文化，并将之有效地应用，那将达到更好的教学目的．

总之，当数学文化的魅力真正渗入客堂、融入教学时，数学就会变得可爱，学生才会喜欢数学．

［1］张楚廷．数学文化［M］．北京：高等教育出版社，2000．

［2］张顺燕．数学的源和流［M］．北京：高等教育出版社，2000．

［3］顾沛．数学文化［M］．北京：高等教育出版社，2000．

［4］史书中．数学与经济［M］．大连：大连理工大学出版社，2000．

［5］蔡亲朋等．数学教育学［M］．杭州：浙江大学出版社，2000．

［6］［美］S．T．坦．应用微积分［M］．北京：机械工业出版社，2004．

［7］羡绪门．管理会计学［M］．天津：科学技术出版社，1984．

Abs tra c t：Mathematics is an important tool for human scientific development．However，it is hard for students in adult university to learn mathematics well．Traditional teaching mode makes it difficult for teacher to teach and difficult for student to learn．Therefore，mathematics of adult university becomes a subject which should be studied by adult educators．This article discusses the necessity and feasibility of introducing mathematical culture into mathematics education in adult university，teaching mathematics in accordance with applied problems，and improving mathematical quality of students through mathematical culture．

Ke y w or d s：adult education；course of Mathematics；mathematical culture；mathematical quality

Feeling Mathematical Culture，Improving Mathematical Quality

ZHANG Yi－ping，MENG Dong－mei，LIU Hai－tao

（Tianjin Xinhua Staf f and Workers University，Tianjin 300040 China）

O1－0

A

1673－582X（2011）01－0117－04

2010－09－14

张艺萍（1964－），女，天津市人、新华职工大学副教授、理学硕士、主要从事高等数学教学及教研、数学文化的研究与实践；孟冬梅（1970－），女，天津市人、新华职工大学副校长、副教授、工学硕士、主抓理工类教学工作；刘海涛（1981－），男，河北黄骅人，新华职工大学讲师，理学硕士，主要从事高等数学教学及数学文化研究。