基于点加权最小二乘无网格法的光学成像光传输模型求解

彭 宽, 高新波, 赵 恒, 王晓蕊,屈晓超, 陈多芳, 陈雪利, 梁继民

1.西安电子科技大学电子工程学院，西安710071；

2.西安电子科技大学生命科学与技术学院，西安710071；

3.西安电子科技大学技术物理学院，西安7100071

基于点加权最小二乘无网格法的光学成像光传输模型求解

彭 宽1,2, 高新波1, 赵 恒2, 王晓蕊3,屈晓超2, 陈多芳2, 陈雪利1,2, 梁继民2

1.西安电子科技大学电子工程学院，西安710071；

2.西安电子科技大学生命科学与技术学院，西安710071；

3.西安电子科技大学技术物理学院，西安7100071

漫射方程是目前光学成像中应用最广泛的光传输模型，通常采用有限元方法进行求解。但是，有限元方法依赖于对整个求解域的网格剖分，而对于类似生物组织的非规则形状求解域的网格剖分是非常困难的，甚至昂贵的商业软件也难以很好地处理。本文将点加权最小二乘无网格法应用于漫射方程的求解。这种方法只需要在求解域内布置一系列规则分布的配点即可进行数值求解，从而可以完全避免有限元方法中困难的剖分工作。此外，这种方法通过最小化控制方程和边界条件在每个配点上产生的残量加权平方和，建立光源功率和光流率密度之间的关系，不需要进行任何数值积分运算，非常适合应用于非规则求解域的求解。基于数字鼠模型的数值仿真实验验证了该方法的准确性和有效性。

无网格法；漫射方程；光传输模型；光学成像

引 言

作为一种新兴的成像技术，分子影像在近10年来获得了飞速发展，并已经在疾病诊断、肿瘤检测和药物研发中获得了广泛应用[1]。它可以从分子和细胞水平上实现对生物有机体生理变化的实时、无创、动态的成像，为特定基因功能、生物体生长发育、疾病发生发展，以及药物作用效果和动力学变化等研究提供了获取信息的有效手段[1]。其中光学分子成像技术由于其在成像灵敏度、性价比和安全性等方面的优势，已经成为分子影像领域新的研究热点[2～5]。

光学成像的核心问题之一是如何对光在生物组织中的传输情况进行准确建模和快速求解。辐射传输方程 (radiation transfer equation，RTE)可以准确地描述光在生物组织中的传输过程，但它的求解难度和求解计算量非常大，因而目前无法应用于实际问题[6,7]。RTE的一种低阶近似——漫射方程(diffusion equation，DE)的求解计算量远远小于RTE，在组织光学特性参数满足漫射条件，即约化散射系数远大于吸收系数时，具有可接受的计算精度。由于很多生物组织的光学特性参数满足漫射条件，因此DE成为了目前光学成像中应用最为广泛的一种光传输模型[6,7]。

考虑到光学成像的实际需要，对DE的求解大多采用数值方法。其中有限元方法 (finite element method，FEM)是最为常用的数值求解方法[6～8]。有限元方法严重依赖于对整个求解域的网格剖分，但对于光学成像中常见的非规则形状求解域，网格剖分是一个极为复杂和困难的过程[6]，通常需要借助专业的商业软件，在某些极端情况下，商业软件甚至都会出现剖分失败的现象。本文提出了一种基于点加权最小二乘无网格法 (point weighted least-squares，PWLS)[9]的DE数值求解方法。通过移动最小二乘方法为每个配点构造近似函数，用在求解域内规则布置的配点代替有限方法中的网格单元，从而彻底避免了对求解域内的网格剖分问题。此外，本文提出的方法通过最小化控制方程和边界条件在所有配点上产生的残量加权平方和，构造生物组织中光源功率和光流率密度之间的关系，不需要进行任何数值积分，因而能够很容易地处理非规则形状的求解域。

理论与方法

漫射方程及其边界条件

如果生物组织的光学特性参数满足漫射条件，则稳定光源发出的光在其中的传输情况可以用如下稳态漫射方程表示[10]：

其中，μa为吸收系数，D=1/(3μa＋3μs′)为漫射系数，μs′为约化散射系数，Φ 为光流率密度，S为光源功率密度。

如果光学成像在全黑的环境中进行，即没有环境光从外部进入生物组织，如下Robin边界条件可以用于描述光在生物组织边界的边界效应[11]：

其中，An为生物组织与空气之间的折射率失配系数，V为生物组织边界单位外法向量。

移动最小二乘近似函数的构造

移动最小二乘近似是一种常见的无网格近似函数构造方法，它根据配点周围采样点上的二次误差和最小的原则，为每个配点构造近似函数[12]。在这种方法中，首先通过如下多项式基函数的线性组合来表示配点i上光流率密度Φi的近似函数：

其中，Pig为基函数向量在第i个配点的第g个采样点上的值；G为一个配点周围采样点的个数；wig是一个非负的权值函数，由配点-采样点间距与采样点的影响域半径的比值r决定。本文采用了如下的权值函数：

在本文中，离某个配点最近的27个配点构成了它的采样点，采样点的影响域半径定义为离采样点最近的27个配点中最远的采样点-配点间距的1.8倍。通过∂J/∂=0最小化J，可以获得如下的线性方程组：

其中，为配点周围采样点上的光流率密度向量，ai为待求的系数列向量。通过式(6)可求解出待求系数向量ai=(Ai)－1BiΦi，将其带入式(3)，即可获得某个配点上的近似函数：

其中，Ni=P(Ai)－1Bi为移动最小二乘近似的形函数。

点加权最小二乘无网格法

将求解域中配点i和边界上配点j的移动最小二乘近似函数代入DE和Robin边界条件，即可获得其对应的控制方程残量和边界条件残量：

其中，列向量Si为配点i周围采样点上的光源功率密度。然后对求解域中所有配点的控制方程残量与边界上所有配点的边界条件残量进行加权平方求和[9]：

其中，Φ和S分别为所有区域配点上的光流率密度和光源功率密度。在光学成像的光传输模型求解中，S被认为是已知量，通过式(12)即可求解出Φ。

实验和结果

我们分别用基于数字鼠模型的匀质和非匀质数值仿体测试了本文方法的性能，并通过与FEM方法求解结果的对比来验证方法的有效性。此外，由于蒙特卡洛 (Monte Carlo，MC)方法在描述生物组织光传输方面具有很好的精度[6,13～15]，它的求解结果被作为评价求解精度的基准。均方根误差e被用来衡量两组归一化数据d1和d2之间的误差：

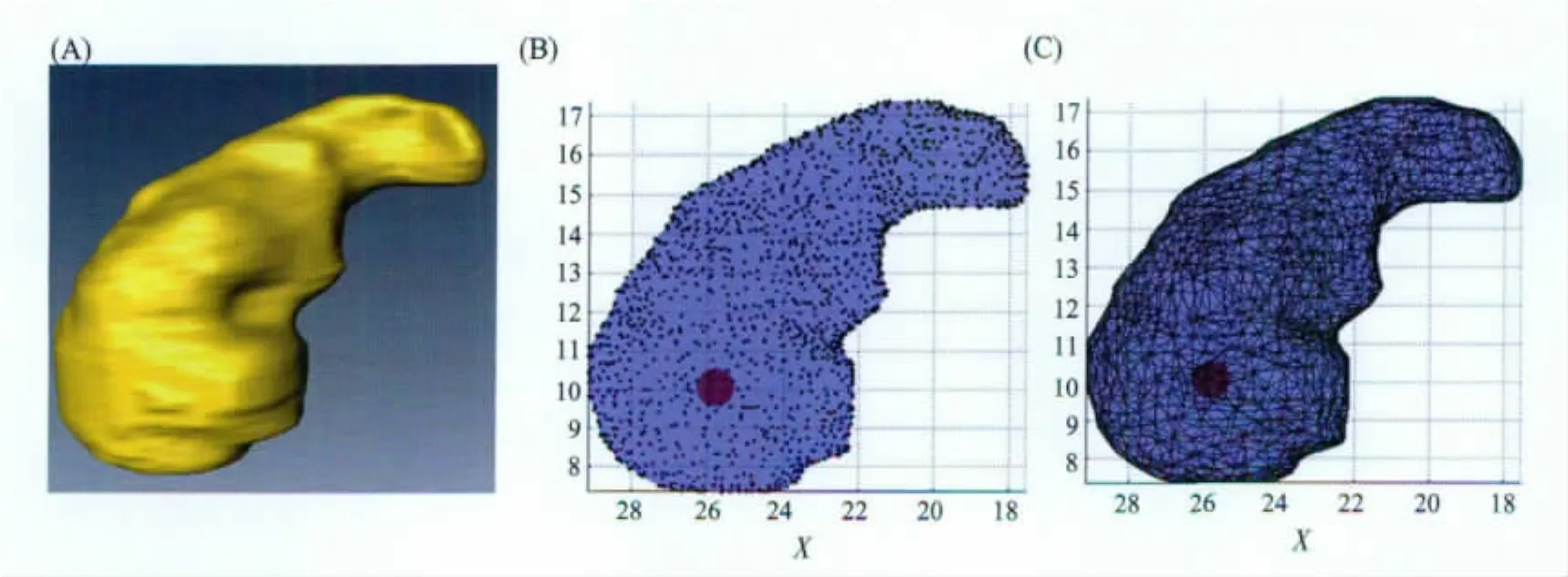
图1 基于小鼠胃部几何形状构建的匀质仿体及其离散情况 (A)小鼠胃的几何结构；(B)PWLS方法中基于配点的仿体离散；(C)有限元方法中基于网格的仿体离散Fig.1 The homogeneous phantom based on the mouse stomach and its discretization (A)Geometrical structure of mouse stomach;(B)The phantom discretization based on collocation points for PWLS;(C)The phantom discretization based on mesh for FEM

匀质仿体的求解

在本实验中，文献[16]中提供的数字鼠胃部CT数据被用来构造匀质仿体，其形状如图1A所示。首先提取区域的边界，并通过三角形进行离散。基于这个离散化的边界，对整个仿体进行四面体网格剖分以生成FEM方法所需的网格。本实验中，PWLS方法所需的配点通过自己的代码布设，其中边界配点直接使用了边界离散三角形的顶点，内部的配点则以0.5 mm的分辨率均匀布设，对整个仿体的离散一共使用了3283个配点，如图1B所示。FEM方法所用的网格中包含了4110个节点和19572个四面体，如图1C所示。MC方法则不需要对求解域的内部进行离散，直接使用前面提到的三角形离散表面即可，MC方法中使用的光源光子随机样本数为108。一个半径为0.5 mm的球形光源被放置于(25,55,10)mm处。根据文献[17]，整个仿体被设置为小鼠胃壁的光学参数，如表1最后一行所示。由于MC方法难以获取仿体内部的光流率密度分布，我们只比较三种方法获取的仿体边界光流率密度。PWLS、FEM与MC三种方法获得的归一化的边界光流率密度如图2所示，可见三种方法获得了非常相似的结果。为了进一步比较三种方法获得的结果，我们取出三种方法在位于z=(10±0.3)mm和z=(13±0.3)mm两个区域内的边界离散三角形顶点上所获结果进行曲线比较，如图3所示。在图3A中，PWLS方法与MC方法在两条曲线上的均方根误差为1.08%；在图3B中，FEM方法与MC方法在两条曲线上的均方根误差为1.63%。由于PWLS方法中所用的配点个数少于有限元网格中的节点数，可见PWLS方法在离散精细度较低的情况下反而获得了比FEM方法稍好的结果。

表1 数字鼠各组织的光线参数Table 1 Optical parameters of the mouse tissue

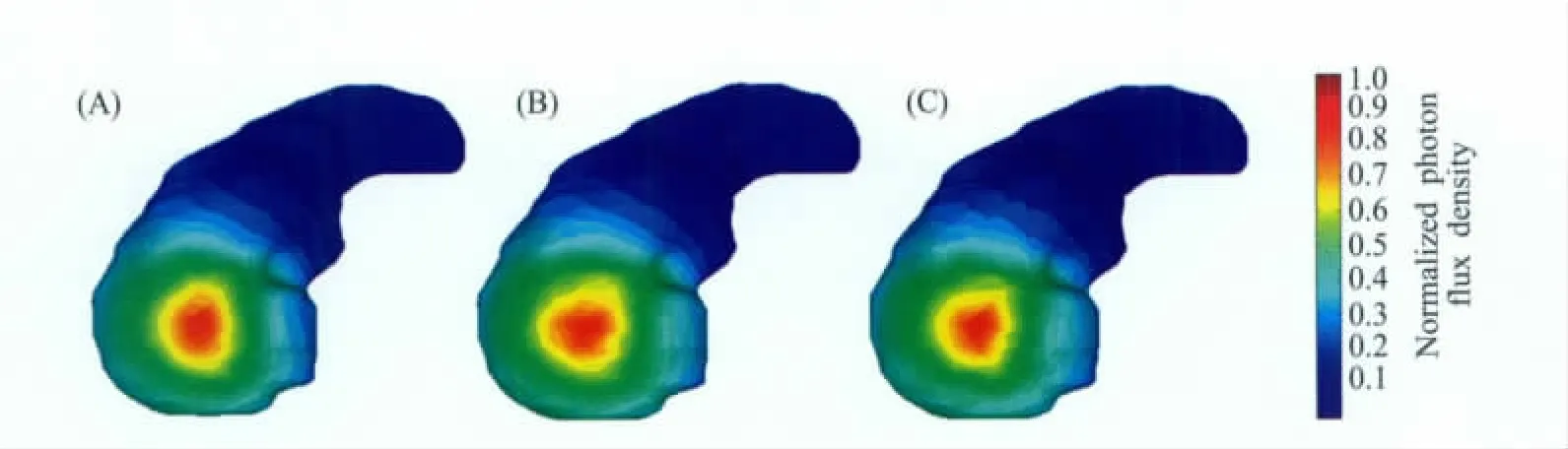
图2 PWLS、FEM与MC三种方法在匀质仿体表面获得的归一化的光流率密度 (A)PWLS方法的结果；(B)FEM方法的结果，(C)MC方法的结果Fig.2 Normalized photon flux density on the surface of homogeneous phantom (A)Result of PWLS;(B)Result of FEM;(C)Result of MC

图3 对PWLS、FEM与MC三种方法在匀质仿体表面获得的归一化的光流率密度的曲线比较 (A)PWLS方法与MC方法的曲线结果；(B)FEM方法与MC方法的曲线结果Fig.3 Curve comparisonsof the normalized photon flux densityon homogeneous phantom surface between PWLS,FEM and MC results (A)Comparison between PWLS and MC results;(B)Comparison between FEM and MC results

非匀质仿体的求解

在这个实验中，我们使用自主研制的Micro-CT系统 (X-ray tube：series 5000 apogee，OXFORD instruments；Flat plane X-ray sensor：C7921CA-02，HAMAMATSU) 所获取的小鼠躯干CT数据来构造非匀质仿体。这个CT数据切片数为256，分辨率为512×512，其中一共包含了脂肪、心脏、肺、肝和肾五种不同的生物组织，如图4所示。由于各种组织

图4 基于小鼠躯干几何形状构建的非匀质仿体及其离散情况 (A)小鼠躯干的几何结构；(B)PWLS方法中基于配点的仿体离散；(C)有限元方法中基于网格的仿体离散Fig.4 The heterogeneous phantom based on the structure of mouse trunk (A) Tissuegeometrical information of the mouse trunk; (B) The phantom discretization with collocation points;(C) The phantom discretization with mesh

之间CT数据对比度不高，各种组织的分割需要人工干预。根据文献[17]，设置各个组织光学参数，如表1中1～5行所示。与上个实验类似，由三角形离散的各个组织的表面首先被提取出来，然后再进行四面体剖分或配点布置。其中，FEM网格中包含6357个节点和34791个四面体；而PWLS方法则使用了分辨率为2 mm的4673个配点。两种方法的仿体离散结果如图4所示。MC方法需要使用各个组织经过三角形离散的表面，所用的光源光子随机样本数仍为108。本实验中所使用的光源为椭球形，三轴半径分别为1.5、1.5和5 mm，其中心位于(29,23,26)mm。PWLS、FEM与MC三种方法获得的归一化的边界光流率密度如图5所示。从图中可见，虽然三种方法获得了非常相似的数据分布趋势，但在光斑的中心区域出现了一定的差别。这是由于小鼠躯干中所包含的肝组织的吸收系数较大，明显不满足约化散射系数远大于吸收系数的漫射条件，从而导致DE方程的准确性下降造成的。与上个实验类似，我们同样取出三种方法在位于z=(27±1)mm和z=(35±1)mm两个区域内的边界离散三角形顶点上所获结果进行曲线比较，如图6所示。从图中可以看出，由于前面提到的原因，PWLS和FEM的计算精度相比上一个实验都有所下降，两个方法在两条曲线上与MC方法的均方根误差分别达到了1.83%和2.26%，但PWLS方法仍然用较低的离散精细度达到了稍好于FEM的计算精度。

图5 PWLS、FEM与MC三种方法在非匀质仿体表面获得的归一化的光流率密度(A)PWLS方法的结果；(B)FEM方法的结果；(C)MC方法的结果Fig.5 Normalized photon flux density on the surface of heterogeneous phantom(A)Result of PWLS;(B)Result of FEM;(C)Result of MC

图6 对PWLS、FEM与MC三种方法在非匀质仿体表面获得的归一化的光流率密度的曲线比较 (A)PWLS方法与MC方法的曲线结果；(B)FEM方法与MC方法的曲线结果Fig.6 Comparisons of the normalized photon flux density on heterogeneous phantom surface between PWLS,FEM and MC results (A)Comparison between PWLS and MC results;(B)Comparison between FEM and MC results

讨 论

有限元方法是目前最为常用的光学成像光传输模型——DE的求解方法。这种方法依赖于对整个求解域的网格剖分，但对于生物组织这种形状非规则区域，进行网格剖分通常非常困难，即使对商业软件而言也是如此。在本文实验中，在提取了离散的仿体边界之后，对整个求解域进行网格剖分时常常会出现剖分失败的现象，需要反复调整仿体边界离散三角形的数量，才能使网格剖分成功进行，可见对形状非规则区域进行网格剖分的难度。本文提出的基于加权最小二乘无网格法的求解方法，只需布置一系列规则排列的配点来对求解域进行离散，难度远远小于对求解域的网格剖分。此外，本文的方法通过最小化控制方程和边界条件在每个配点上产生的残量加权平方和，建立光源功率和光流率密度之间的关系，不需要进行任何形式的数值积分，大大地方便了其在生物组织这种形状非规则区域中的应用。

在实验中可以发现，本文的方法可以用较低的求解域离散度，实现与有限元方法相当的求解精度。这是因为无网格法中配点近似函数的构造考虑了周围27个配点，而有限元网格中每个节点的近似函数构造只受与其共单元的节点影响，其数量通常不到20个。因此，每个配点近似函数中可以包含更多的信息量，从而降低离散整个求解域所需的配点数量。由于最后获得的系统方程组的维数与用于离散求解域的节点或配点个数相等，在保证计算精度的前提下使用了较少的配点数量，显然可以降低求解的内存消耗与计算量。

最后，在第二个实验中，我们发现DE作为小鼠全身成像光传输模型时，也存在一定的局限性：由于小鼠中一部分组织的光学特性参数并不满足漫射条件，应用DE有可能导致求解精度的下降。这就要求在小鼠成像中使用不受漫射条件限制的RTE的高阶近似形式，如简化球谐波、球谐波和离散坐标等[6,18]，但这些高阶近似方程的计算量都较大，如何提高它们的求解速度将是一个非常值得研究的问题。

1. Cherry S.In vivomolecular and genomic imaging:New challenges for imaging physics.Phys Med Biol,2004,49:13～48

2. Weissleder R,NtziachristosV.Shedding light onto live molecular targets.Nat Med,2003,9:124～128

3. Bhaumik S, GambhirSS. Optical imaging of Renilla luciferase reporter gene expression in living mice. Proc Natl Acad Sci USA,2002,99:377～382

4. Massoud TF,Gambhir SS.Molecular imaging in living subjects:Seeing fundamental biological processes in a new light.Genes Dev,2003,17:545～580

5. RiceW,CableMD,NelsonMB.Invivoimagingof light-emitting probes.J Biomed Opt,2001,6:432～440

6. Gibson AP,Hebden JC,Arridge SR.Recent advances in diffuse optical imaging.Phys Med Biol,2005,50:1～43

7.Wang G,Cong W,Li Y,Han W,Kumar D,Qian X,Shen H,Jiang M,Zhou T,Cheng J,Tian J,Lv Y,Li H,Luo J.Recent development in bioluminescence tomography.Curr Imaging Rev,2006,2:453～457

8. Arridge SR,Dehghani H,Schweiger M,Okada E.The finite element modelfor the propagation of light in scattering media: A directmethod fordomains with nonscattering regions.Med Phys,2000,27:252～264

9. Wang Q, LiH, Lam K. Developmentofa new meshless-point weighted least-squares(PWLS)method for computationalmechanics. ComputMech, 2005, 35:170～181

10. Ntziachristos V, Tung C, BremerC, WeisslederR.Fluorescence molecular tomography resolves protease activityin vivo.Nat Med,2002,8:757～760

11.Schweiger M,Arridge SR,Hiraoka M,Delpy DT.The finite element method for the propagation of light in scattering media:Boundary and source conditions.Med Phys,1995,22:1779～1792

12.Belytschko T,Krongauz Y,Organ D.Meshless methods:An overview andrecent developments. Comput Method Appl Mech Eng,1996,139:3～47

13.WangL,JacquesSL,ZhengL.MCML-MonteCarlo modeling ofphoton transportin multi-layered tissues.Comput Meth Prog Biomed,1995,47:131～146

14.Boas D,Culver J,Stott J,Dunn A.Three dimensional MonteCarlo code for photon migration through complex heterogeneous media including the adult human head.Opt Express,2002,10:159～169

15.Ren NN,Liang JM,Qu XC,Li JF,Lu BJ,Tian J.GPU-based Monte Carlo simulation for light propagation in complex heterogeneous tissues.Opt Express,2010,18:6811～6823

16. Dogdas B, StoutD, Chatziioannou A, Leahy RM.Digimouse:A 3D whole body mouse atlas from CT and cryosection data.Phys Med Biol,2007,52:577～587

17. Alexandrakis G, Rannou FR, Chatziioannou AF.Tomographic bioluminescence imaging by use of a combined optical-PET (OPET) system: A computer simulation feasibility study. Phys Med Biol, 2005, 50:4225～4241

18.Klose AD,Larsen EW.Light transport in biological tissue based on the simplified spherical harmonics equations.J Comput Phys,2006,220:441～470

Point Weighted Least-Squares Meshless Method for Photon Transport in Complex Biological Tissues

PENG Kuan1,2,GAO Xinbo1,ZHAO Heng2,WANG Xiaorui3,QU Xiaochao2,CHEN Duofang2,CHEN Xueli1,2,LIANG Jimin2
1.School of Electronic Engineering,Xidian University,Xi'an,710071,China;
2.Life Sciences Research Center,School of Life Sciences and Technology,Xidian University,Xi'an 710071,China;
3.School of Technology Physics,Xidian University,Xi'an 710071,China

This work was supported by grants from the"973"Program(2011CB707702),the National Natural Science Foundation of China(81090272,81000632,30900334,60771068),the Shaanxi Provincial Natural Science Foundation Research Project(2009JQ8018),and the Fundamental Research Funds for the Central Universities

Nov 1,2010 Accepted:Jan 18,2011

LIANG Jimin,Tel:+86(29)81891060,E-mail:jimleung@mail.xidian.edu.cn

Diffusion equation is a widely used model for photon transport in biological tissues.Commonly,it can be solved by the finite element method,which depends on the mesh discretization of interesting area.However,this kind of discretization is quite difficult for complex geometries such as biological tissues,even using commercial software.In this paper,a point weighted least-squares(PWLS)meshless method for the photon transport in diffusive biological tissueswith complex and irregular geometriesis presented. The proposed method doesthe calculation with some collocation pointsdistributed regularly in the interesting area,so that complicated mesh generation required by finite element method can be avoided.Moreover,our method establishes the relationship between the source distribution and the photon flux density by minimizing the weighted residuals quadratic sum of all collocation points. Thus, it doesn't need the complicated integration calculation,which provides more convenience for the application in irregular shaped region like biological tissues.Numerical simulations with the phantoms constructed based on mouse tissues demonstrate the accuracy and effectiveness of the proposed method.

Meshless method;Diffusion equation;Light transport model;Optical imaging

2010-11-01；接受日期：2011-01-18

“973”计划项目(2011CB707702)，中国科学院百人计划，国家自然科学基金项目(81090272，81000632，30900334，60771068)，陕西省自然科学基础研究计划项目(2009JQ8018)，中央高校基本科研业务费专项资金资助

梁继民，电话：(029)81891060，E-mail：jimleung@mail.xidian.edu.cn

TP-391

10.3724/SP.J.1260.2011.00373