外墙环境温度效应分析研究

李 晶 佟 磊

（1．沈阳化工研究设计有限公司，辽宁，沈阳，110000）

（2．沈阳沈飞建设置业有限公司，辽阳，沈阳，110000）

外墙环境温度效应分析研究

李 晶1佟 磊2

（1．沈阳化工研究设计有限公司，辽宁，沈阳，110000）

（2．沈阳沈飞建设置业有限公司，辽阳，沈阳，110000）

本文只考虑墙体混凝土龄期达一个月后对其进行分析，并结合“王铁梦法-温度应力计算公式”研究墙体在环境温度变化以及同时期内混凝土收缩、徐变下的结构效应(应力、应变等)—本文统一称之为“环境温度效应”。本文以沈阳市气候特点为研究聻景，找出最不利时的季脧温差从而计算出外墙环境温度收缩应力。

环境温度效应；最不利温差；环境温度收缩应力

一、概述

对于很多实际墙体工程在完工后半年或一年多才出现裂缝，建筑物外墙受季节温差影响很大，所以考虑季节温差引起的温度应力是很有必要的。气温的变化是引起混凝土裂缝的另一重要原因，也是计算温度应力和制定温度控制措施的重要依据。

四季气候变化引起的温度变化则需要结构所在地点的气候资料，一般可以从当地气象局得到。设计过程中可以按最不利条件考虑。其中按最不利气候条件产生的季节气候变化引起的温度应力是非常大的，这在裂缝控制设计时应该予以重视。对本文所研究的墙体，其温度场的变化值将参照沈阳市气象统计资料并根据民用建筑热工设计规范中的相关条文来确定。

收缩是混凝土材料的一个固有性质，在混凝土中是普遍存在的。由于钢筋混凝土结构中混凝土具有收缩性质而钢筋没有，因此钢筋将对混凝土的收缩产生阻碍作用，从而使钢筋受压而混凝土受拉，当截面中配筋过多时，这种混凝土内的拉应力也不可忽略。

由于温度变化和混凝土收缩作用的时间都很长，由于温度的变化是缓慢的，尤其在考虑季节温差对墙体的影响时，同时混凝土的收缩也是随时间的推进而缓慢发展的，因此分析中必须考虑混凝土徐变的影响。

二、环境温度变化与墙体上的温度分布

1、墙板温度分布变化

由于墙体在厚度方向上的几何尺寸相对很小，所以墙板内部各点的温度变化受外界温度变化影响敏感。季节温度变化也将引起结构物温度的变化，由于这种变化的长期性和缓慢性，可认为是结构整体发生均匀的温度变化。所以，在考虑季节温度变化对结构物的影响时，均以结构物内的平均温度为依据。内外温差变化应力分布变化较大，这种非线性温差产生的温度应力主要原因是寒潮来袭气温骤降。

2、墙体内的温度分布与计算用温差的取值

整体温差越大，产生的结构效应越不利，对内外温差也一样。在确定这种温差的设计计算值时，需要对相关数据进行统计分析，沈阳市气象资料就是重要的参考资料。

依据上述分析，需要确定的值有墙板初始温度和墙板温度整体变化内外表面的最大温差。

（1）墙体的初始温度

墙体初始温度的取值方法各异，但本文研究的是强度和弹性模量均达稳定时墙体的平均温度为初始温度。研究墙体在六月中旬浇筑，一个月后适值气温最高的七月，七月的平均气温可将墙体初始温度定为25℃。

（2）墙体温度整体变化时的最大温差

墙体温度的整体变化有升温和降温两种。墙整体升温将使混凝土内产生压应力，而整体降温则产生拉应力，可能使墙体拉裂，对墙体更为不利。因此本文在考虑墙体温度整体变化时只考虑整体降温而不再考虑整体升温这种情况

墙体温度整体变化时按均匀温差作用考虑，均匀温差是指结构物内外构件和构件内外温度变化基本相同，主要由季节温差引起。季节温差指混凝土浇筑成型阶段的施工温度(对于设有后浇带的工程取后浇带封堵时的温度)与后期各个阶段温度的差值，它变化长期缓慢，结构整体温度变化均匀，故考虑其对结构影响时，均以结构的平均温度为依据。具体可按下式计算:∆ T =Tmax( Tmin−To其中 Tmax(Tmin)指最热月(最冷月)平均温度，To指混凝土浇筑成型时的平均温度。本文 To=25℃，则 ∆ T =Tmin−To进制=-11-25=36℃。

三、混凝土的收缩变形及当量温差的计算

混凝土随着多余水分的蒸发必将引起体积的收缩，其收缩量甚大，机理比较复杂，随着许多具体条件的差异而变化，根据国内外统计资料，可用下列指数函数表达式进行收缩值的计算:

由于湿度不均匀，收缩变形也随之不均匀，基础的平均收缩变形助长了温度变形引起的应力，可能导致混凝土开裂。因此在温度应力计算中必须把收缩这个因素考虑进去。为了计算方便，把收缩换算成“收缩当量温差”。就是说收缩产生的变形，相当于引起同样变形所需要的温度:。即本文在计算中考虑的墙体混凝土的收缩当量温差为18.45‡。

四、单扇墙体降温和收缩当量温差作用下温度收缩应力的计算

王铁梦在 1974年推导出了长墙及地基板的温度收缩应力计算公式(以下称王铁梦公式)，可用于墙和地基板整体温度变化时产生的温度应力的估算，至今在工程实践中仍得到广泛应用。

王铁梦公式中的墙体为一浇筑在混凝土基础上的长墙，其它边界面均为自由，其厚度远小于其它两个方向尺寸，所推导出的公式为(推导过程略)[1]。

由季节性温度变化引起的墙整体降温，墙体温度整体变化时的最大温差为36℃，墙体混凝土的收缩当量温差为18.45‡。由于这两种温差都使墙体受拉，将产生相同的结构效应，因此可将两者合并为一项，即同时考虑由季节性温度变化引起的墙整体降温和混凝土收缩的不利影响时，应分析最大达54.45℃的温降。用王铁梦公式计算该温差引起的墙体内最大温度应力，各参数取值如下：

混凝土的强度等级为 C40，E=3.25×104N/mm2， =1×10-5/℃，T=54.45℃，H=3200mm， H ( t ,τ)=0.3，对于 CX值王铁梦建议取100×10-2~150×10-2N/mm3，因此本文分别取CX1=100×10-2N/mm3，和CX2=150×10-2N/mm3进行计算；对墙长L分别取不同的值。 计算结果如表1-1所示。图1-1所示为不同CX值下计算所得σm*ax值随墙长变化情况。

表1-1 不同长度墙体用王铁梦公式计算所得σmax、σm*ax值(单位:MPa)

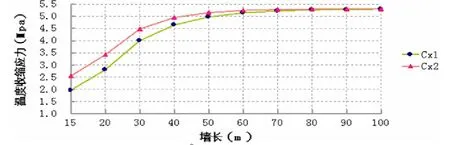
图1-1 计算所得*maxσ值随墙长变化示意图

从图1-1中可以发现计算所得最大温度应力值随墙长的增加而加大，但在墙长增加到70m以后时应力变化趋缓，并趋向于*maxσMPa3.5=即可忽略差异的存在。

温度产生的超静定内力与混凝土的徐变有关，混凝土的徐变将大大减少温度在混凝土结构中产生的内力。这一点是温度应力与荷载应力不同的地方，考虑这一点将使结构的配筋大大的减少。

[1] 王铁梦. 工程结构裂缝控制.中国建筑工业出版社,1997.8

[2] 徐荣年，徐欣磊.工程结构裂缝控制—“王铁梦法”应用实例集.中国建筑工业出版社,2005

[3] 沈阳市建设标准 SYJG 2007-1.超长地下室混凝土结构防裂技术规定.沈阳市城乡建设委员会, 2007

TU548

A

1674-3954（2011）02-0029-02