可靠性灵敏度分析的一种偏倚蒙特卡罗方法

李静辉 康 锐

(北京航空航天大学 可靠性与系统工程学院，北京 100191)

Ali Mosleh

(美国马里兰大学帕克分校 风险与可靠性中心，马里兰 20742)

在可靠性分析中，除获得系统不可靠度等指标之外，通常还希望知道这些指标对相关参数(如元件的失效率和修复率等)的灵敏程度(相关导数).

可靠性灵敏度分析的一种传统方法是进行解析地求导计算，但这种解析方法一般只对比较简单的系统才可行，对于规模较大和较复杂的系统，通常需要借助于仿真.与系统不可靠度等非导数指标的估计相比，如何通过仿真获得相关导数的估计目前研究相对较少.一种比较直接的方法是有限差分法［1］，但当感兴趣的参数较多时，有限差分法需要运行很多轮仿真;此外，差分步长的选取涉及著名的“偏差－方差”难题.文献［2］中探讨了一种只需运行一轮仿真的方法，但仍存在差分步长的选取问题.而且对于高可靠度系统，原始蒙特卡罗仿真的效率一般会很低，需要采取降低方差技巧来加速仿真.文献［3－5］等针对考虑修复的高可靠度马尔可夫型系统的可靠性灵敏度分析进行了讨论，并考虑了方差问题，但并没有专门针对导数估计方差降低技巧的探讨，而是直接利用降低非导数指标估计方差的技巧来同时减小导数估计的方差.

本文立足经典可靠性系统，探讨应用仿真进行可靠性灵敏度分析的方法，并提出一种直接从降低导数估计方差出发的偏倚技巧来加速仿真.

1 导数估计方法选择

本文主要考虑系统不可靠度(也称为失效概率或累计失效概率)及其对相关参数导数的估计.一般地，系统不可靠度可表达成如下数学期望的形式:

式中，θ为参数向量;I{ω∈R}为指示函数;Ω为样本空间;ω为样本点;R为样本空间中的系统失效域;f(θ，ω)为Ω上的概率密度函数.根据式(1)，系统不可靠度ℓ(θ)可采用标准的蒙特卡罗仿真进行估计:

进一步，需要估计ℓ(θ)对相关参数的导数:

θj为参数向量 θ =(θ1，θ2，…，θd)的第 j个分量;d为参数的个数.为简化起见，下文有时将∂ℓ(θ)/∂θj简记为.

本文关心的系统不可靠度对相关参数的导数估计具有如下几个需求和特点:

1)感兴趣的参数出现在概率分布中;

2)涉及的参数个数可能较多;

3)ℓ(θ)为一指示函数的数学期望，而指示函数具有不光滑、难以变换处理等病态性质;

4)对于高可靠度系统，为获得满意精度的估计，可能需要运行大量次数的仿真.

目前文献中已经提出一些可以用来估计如式(1)所示的数学期望对相关参数导数的仿真方法［6－8］，主要有:有限差分方法［1］、扰动分析方法［9－10］、似然比方法［11－12］和弱导数方法［13－15］.这些导数估计方法近年来在排队系统、库存模型和金融等领域中受到广泛关注，但对于这些方法在可靠性分析中的应用，目前相关探讨仍然较少.

在上述各种导数估计方法中，似然比方法较好地满足本文关心的可靠性灵敏度分析的需求和特点.因此，本文选择似然比方法作为基础的导数估计方法.关于似然比方法的详细介绍，可参考文献［11－12］.

2 原始蒙特卡罗似然比导数估计

本节首先推导未采用重要抽样的原始蒙特卡罗仿真环境下的似然比导数估计方法.在应用蒙特卡罗仿真进行可靠性分析时，可选择两种不同的基本形式:基于元件的直接蒙特卡罗方法和基于系统的间接蒙特卡罗方法［16］.本文主要讨论基于元件的直接蒙特卡罗方法，并主要考虑如下类型的经典可靠性系统(模型):设系统由n个元件组成，各元件依次编号为1，2，…，n，初始时所有元件均处于正常工作状态，假设各元件之间相互独立，且寿命均服从指数分布，即 fj(t)=λje－λjt(λj为元件j的失效率)，任务时间为T，感兴趣的量为系统不可靠度及其对各元件失效率的导数.

基于元件的直接蒙特卡罗方法从元件层次来模拟系统的行为，直接从相应的分布产生每个元件转移时间的抽样.记元件j抽样到的转移时间为tj(j=1，2，…，n)，由全部 tj可以确定一个具体的系统轨迹ω，对于每一个ω，可以判断系统最终是成功还是失效，从而获得I{ω∈R}的值(0或1).在整个仿真结束之后，计算式(2)可获得系统不可靠度的估计.

为利用似然比方法获得系统不可靠度对各元件失效率的导数，可取 ω =(t1，t2，…，tn)，ω 的概率密度为

将式(4)对λj求导，可得

从而

式(6)中Sλj(θ，ω)为统计学中著名的得分函数.根据似然比方法原理，可获得ℓλj的无偏估计量:

3 一种利用结构函数的偏倚技巧

原始蒙特卡罗方法的一个主要缺陷是收敛速度慢，尤其对小概率事件，为获得满意精度的估计，需要运行大量次数的仿真.对比式(2)和式(7)可以看出，导数估计比系统不可靠度本身的估计更具有挑战性.对于高可靠度系统，原始蒙特卡罗仿真采样到的绝大多数系统轨迹ω都不会落入系统失效域R内，这些系统轨迹对各ℓλj贡献的统计得分也都为零.而且，与估计不可靠度ℓ的式(2)相比，估计ℓλj的式(7)还多了一个随机项——得分函数，从而一般会带来更大的方差.可见，导数估计比不可靠度估计本身一般更需要减小方差，以能在合理的时间内获得满意精度的估计.

为降低式(7)中系统不可靠度对各元件失效率导数估计的方差，本文在借鉴文献［17－18］中方法的基础上提出一种利用系统结构函数的偏倚技巧.

设Ij(tj)代表元件 j的状态指示变量，Isys(tsys)代表系统的状态指示变量，其中tj和tsys分别代表元件 j和系统的失效时间，Ij(tj)和Isys(tsys)均定义如下:

一般地，系统状态指示变量可表达成各元件状态指示变量的函数，该函数通常称为系统结构函数.通过对结构函数进行逻辑化简，可表达为

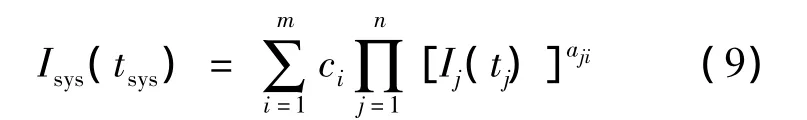
其中，m为结构函数化简后的总项数;ci为第i项前面的系数;aji取0或1:如果第 i项中含有Ij(tj)，则 aji=1，否则 aji=0.

由于在基于元件的直接蒙特卡罗方法中，直接从相应的概率分布fj(t)抽样每个元件的失效时间tj，应用重要抽样的一个自然做法是改变tj的抽样分布.设抽样tj的新的重要抽样分布为(t)，则相应的权重函数为

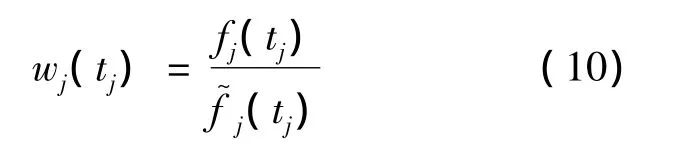
进一步，定义如下估计量:

值得一提的是，在上述证明过程中用到了以下两个等式:

可以验证，在 aji取0和1两种情况下，均有式(16)和式(17)成立.

式(15)意味着可以用

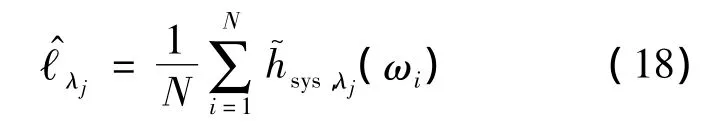
作为ℓλj的近似估计值.

即Br代表式(12)中所有包含的项(亦即结构函数式(9)中所有包含Ir的项)，并可以将Br中的元素按从小到大的顺序排列.进一步，对于r≠j，有

对于 r=j，有

对式(22)和式(23)作进一步整理，可得

由于式(24)和式(25)中第2项总大于0，故有

这意味着，式(19)中系统层次的优化问题可以分解为式(26)和式(27)中元件层次的优化问题，这是式(12)中所定义估计量的一个重要优势，可以避免高维优化的难题.

对于寿命服从指数分布的情形，通过代入各相关变量(式(6)、式(10)、式(11))和一定的变形处理，式(26)和式(27)可分别转化为如下2个非线性方程:

图1 最优偏倚值随自然值Λ的变化曲线

4 实例验证

为验证本文方法的有效性，本节考虑一个可以解析求解的简单实例.系统的可靠性框图如图2所示.

图2 一个简单的串并联混合系统

各元件的失效率为 λ1=1.0 ×10－6/h，λ2=1.5 × 10－6/h，λ3=2.0 × 10－6/h，λ4=8.0 ×10－4/h，λ5=9.0 ×10－4/h，任务时间为 T=1 h.对于该简单系统，不难解析计算出系统不可靠度及其对各元件失效率的导数，相应的计算公式为

另外，采用MATLAB编程实现，应用第2节中描述的原始蒙特卡罗方法和第3节中描述的偏倚蒙特卡罗方法对该实例进行了求解.对于偏倚蒙特卡罗方法，除最优参数组外，还选取了其它几组偏倚参数进行了试验.解析计算和各组蒙特卡罗仿真试验的结果见表1.

对于各组蒙特卡罗仿真试验，表中第1行为估计值，第2行为估计方差和相对误差(均为样本值)，其中相对误差根据下式计算:

5组偏倚蒙特卡罗仿真采用的偏倚参数分别为:

① (0.32，0.32，0.32，0.32，0.32)

② (1.60，1.60，1.60，1.60，1.60)

③ (8.00，8.00，8.00，8.00，8.00)

④ (0.32，0.80，1.60，3.20，8.00)

⑤ (0.01，0.015，0.02，8.00，9.00)

其中第②组为最优参数，第①，③，④组由在最优参数的基础上乘上一定的因子(0.2，0.5，1，2，5)得到，第⑤组在各元件自然失效率的基础上同时增大104倍.原始蒙特卡罗的仿真次数为108，5组偏倚蒙特卡罗的仿真次数均为106.

由表1可以看出，各组蒙特卡罗仿真试验基本上都给出了较为合理的估计(各个量的估计值均比较接近其真值).此外，各组蒙特卡罗的估计性能也与预期相符:原始蒙特卡罗的效率较为低下，仿真108次获得的结果精度仍不够理想;5组偏倚蒙特卡罗的效率相对原始蒙特卡罗均有明显的改善，其中对应最优参数组的偏倚蒙特卡罗符合预期地获得了最小的方差和相对误差，与原始蒙特卡罗相比，各个估计量都降低了至少6个数量级的方差.比较5组偏倚蒙特卡罗的估计方差和相对误差可以看出偏倚参数的选取对于估计性能的影响.各组偏倚蒙特卡罗的估计结果基本上符合“偏倚参数离最优值越近，估计精度越高”的规律.特别地，如果一个偏倚参数组相对另一个偏倚参数组“绝对占优”(每个参数都离最优值更近)，仿真结果显示其估计性能也“绝对占优”(对每个量的估计精度都更高).符合这个情况的有第①组相对第③组和第⑤组、第②组相对所有其余各组以及第④组相对第⑤组.为改善高可靠度系统仿真的效率，一般需要增大失效率，但第③组偏倚蒙特卡罗的试验结果表明，选取太大的失效率(偏倚过度)获得的估计性能可能并不理想(这一组中各个量的估计精度都比第①组和第④组要差至少一个数量级).另外，从第⑤组偏倚蒙特卡罗的仿真结果可以看到，将全部失效率统一扩大一定的倍数虽然是一种便捷的做法(而且在实际中常被仿真分析人员采用，尤其在缺少如何选取偏倚参数的有效指导的情况下)，但其估计性能可能并不是十分理想，特别是当各失效率的大小相差较大时.另一方面，虽然有些组中选取的偏倚参数离最优值不是很接近，但从整体上来看，各组偏倚蒙特卡罗仿真的估计性能都还较令人满意(仿真106次获得的相对误差均小于5%).这主要源于所采用的利用系统结构函数的估计量，该估计量充分利用了系统结构信息，从而可以较为充分地利用仿真过程中产生的抽样信息.另外，由表1可以看出的另一个值得一提的现象是，在同一次蒙特卡罗仿真试验中，不同量的估计性能之间可能存在差异.对于这里考虑的实例，和的估计精度明显比 ℓ，，和 ℓλ3要低.

表1 解析计算和蒙特卡罗仿真估计结果

5 结论

1)似然比方法可以较好地满足可靠性灵敏度分析(导数估计)的需求，能够在一轮仿真中同时估计出系统不可靠度及其对相关参数的导数，并且仅需在估计系统不可靠度的基础上增加较小的计算负担;

2)对于高可靠度系统，似然比导数估计也面临方差问题，需要采取降低方差技巧来加速仿真，事实上，导数量的估计通常比非导数量的估计更需要减小方差;

4)实例分析验证了第3节中提出的偏倚蒙特卡罗方法的有效性，该方法对各个感兴趣的量都给出了很好的估计，与原始蒙特卡罗方法相比，各个估计量的方差都降低了至少6个数量级.

References)

［1］Asmussen S，Glynn P W.Stochastic simulation:algorithms and analysis［M］.New York:Springer，2007

［2］Marseguerra M，Zio E.Monte Carlo estimation of the differential importance measure:application to the protection system of a nuclear reactor［J］.Reliability Engineering and System Safety，2004，86(1):11 －24

［3］Nakayama M K，Goyal A，Glynn P W.Likelihood ratio sensitivity analysis for Markovian models of highly dependable systems［J］.Operations Research，1994，42(1):137 －157

［4］Nakayama M K.Asymptotics of likelihood ratio derivative estimators in simulations of highly reliable Markovian systems［J］.Management Science，1995，41(3):524 －554

［5］Nakayama M K.On derivative estimation of the mean time to failure in simulations of highly reliable Markovian systems［J］.Operations Research，1998，46(2):285 －290

［6］L'Ecuyer P.An overview of derivative estimation［C］//Nelson B L，Kelton W D，Clark G M.Proceedings of the 1991 Winter Simulation Conference.Phoenix:IEEE，1991:207 －217

［7］Fu M C.Stochastic gradient estimation［C］//Henderson S G，Nelson B L.Handbooks in Operations Research and Management Science:Simulation.Boston:Elsevier，2006:575 －616

［8］Fu M C.What you should know about simulation and derivatives［J］.Naval Research Logistics，2008，55(8):723 －736

［9］Ho Y C.Performance evaluation and perturbation analysis of discrete event dynamic systems［J］.IEEE Transactions on Automatic Control，1987，32(7):563 －572

［10］Gong W B，Ho Y C.Smoothed(conditional)perturbation analysis of discrete event dynamical systems［J］.IEEE Transactions on Automatic Control，1987，32(10):858 －866

［11］Rubinstein R Y.Sensitivity analysis and performance extrapolation for computer simulation models［J］.Operations Research，1989，37(1):72 －81

［12］Rubinstein R Y，Kroese D.Simulation and the Monte Carlo method［M］.Hoboken:Wiley，2007

［13］Pflug G C.Sampling derivatives of probabilities［J］.Computing，1989，42(4):315 －328

［14］Heidergott B，Vázquez－Abad F J.Measure－valued differentiation for Markov chains［J］.Journal of Optimization Theory and Applications，2008，136(2):187 －209

［15］Heidergott B，Vázquez－Abad F J，Pflug G，et al.Gradient estimation for discrete－event systems by measure－valued differentiation［J］.ACM Transactions on Modeling and Computer Simulation，2010，20(1):1 －28

［16］Labeau P E，Zio E.Procedures of Monte Carlo transport simulation for applications in system engineering［J］.Reliability Engineering and System Safety，2002，77(3):217 －228

［17］Campioni L，Vestrucci P.Monte Carlo importance sampling optimization for system reliability applications［J］.Annals of Nuclear Energy，2004，31(9):1005 －1025

［18］Campioni L，Scardovelli R，Vestrucci P.Biased Monte Carlo optimization:the basic approach［J］.Reliability Engineering and System Safety，2005，87(3):387 －394