谐波齿轮传动系统刚体动力学模型的建立与分析

时祖光，李玉光，王淑芬

（大连大学 机械工程学院，辽宁 大连 116622）

传统的计算谐波齿轮传动轮齿间的啮合力是把整个齿轮系统做为刚体对待。这样计算出来的啮合力实际上是平均啮合力，不能作为动态分析的载荷谱。要精确计算轮齿之间的动态啮合力就要运用多体系统动力学分析方法。多体系统动力学包括多刚体系统动力学建模、多柔体系统动力学建模、多体系统动力学方程求解及多体系统动力学中的刚性问题等。目前，其刚体部分已做得相当完善，并已形成相对成熟的商业软件。RecurDyn是新一代多体系统动力学计算软件，它采用相对坐标系运动方程理论和完全递归算法，在求解大规模、高速和病态问题方面的性能大大超过了其他的机构动力学分析软件，适合于求解类似谐波齿轮传动的多体系统动力学问题。

1 模型的建立

（1）齿轮几何模型的建立。谐波齿轮几何模型建立的思路是：首先利用Pro/E的二次开发工具模块Program分别绘制刚轮与柔轮，绘制出基准曲线和齿廓线；其次是镜像复制齿廓渐开线，选取两轮的齿顶圆、齿根圆和两条渐开线作为使用边，利用拉伸命令创建第一个轮齿，进而旋转阵列生成齿轮模型；最后创建齿轮的辅助特征，完成一个完整齿的参数化建模。在这个基本齿轮的基础上，通过修改基本参数，得到需要的齿轮三维实体。

（2）传动系统模型的建立。利用Pro/E造型软件，建立好每个零件几何模型后，再利用其装配功能将零部件连接起来，并对装配好的模型进行干涉检查和简单的运动学分析。

2 多刚体动力学分析

谐波齿轮传动系统动力学分析模型是描述系统力学性质的数学表达式，建立分析模型就是对系统动力学模型进行数学化处理，以得到相应的数学表达式。通过这一数学模型，不仅可以准确分析谐波齿轮传动系统齿轮之间啮合力的变化规律，还可以通过查看各轮的运动速度是否符合理论值来验证仿真模型的正确与否。

（1）谐波齿轮传动系统多刚体动力学模型的建立。谐波齿轮传动系统齿轮之间的啮合力是谐波齿轮传动的主要动态特性之一，对系统的动态响应、承载能力、疲劳分析等都具有重要的意义。齿轮之间啮合力的计算一直是分析的难点，由于柔轮变形的原因，导致啮合刚度是变化的，再加上轮齿的啮入和啮出都受冲击载荷等因素的影响，使得仅仅研究齿轮的静态接触力远远达不到设计的要求，因此必须要研究轮齿动态的啮合力。借助RecurDyn软件能精确计算齿轮之间的动态啮合力。

为了简化模型，将齿轮上的辅助支撑去掉。在Pro/E中将齿轮系统模型保存为*.step格式后，利用Import命令即可将模型导入到RecurDyn。谐波齿轮系统模型导入到RecurDyn中后，还不能成为动力学的分析模型。需要在刚轮上施加驱动转速,柔轮上施加负载。为了防止启车时转速和负载的突变，驱动和负载都用渐进函数step函数施加。最后，利用Recur-Dyn中提供了专门用于接触分析的接触模块(contact)来定义齿轮之间的接触。

（2）谐波齿轮系统多刚体动力学仿真。RecurDyn中计算接触力的公式为：fn=k×δm1+c×

K和C分别为刚度和阻尼系数；m1,m2,m3分别是刚度、阻尼和缺陷的非线性力指数；δ是相接触的两物体的渗透量；是渗透量对时间的导数。考虑到轮齿厚度将δ定为1mm；在仿真前先预估下啮合力的大小，根据公式fn=K*δ来定义大概的接触刚度系数K的值。

刚轮齿数Z1=26，柔轮齿数Z2=28。 理论计算出来的转速值和仿真出来的值对比结果如表1所示。

由表1可以看出，仿真出的转速和理论值在误差允许范围内是一致的，并且各个部件的转速波动也比较小，符合实际情况。理论的静态啮合力Fn用式（2）计算：

利用上式就可以计算出每个齿轮副的啮合力。仿真出来的啮合力曲线如图1所示。

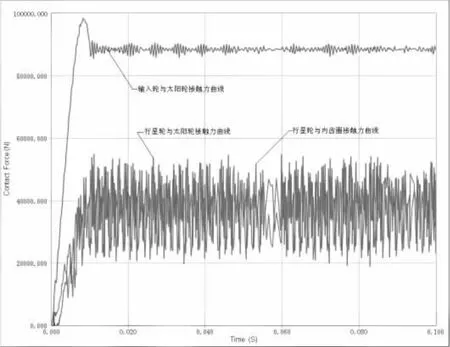
图1 啮合力曲线

在0～0.01s时是系统的启动阶段，转速和接触力逐渐上升，0.01秒之后是平稳阶段。理论接触力与仿真接触力的数值及其误差的具体计算结果见表2。

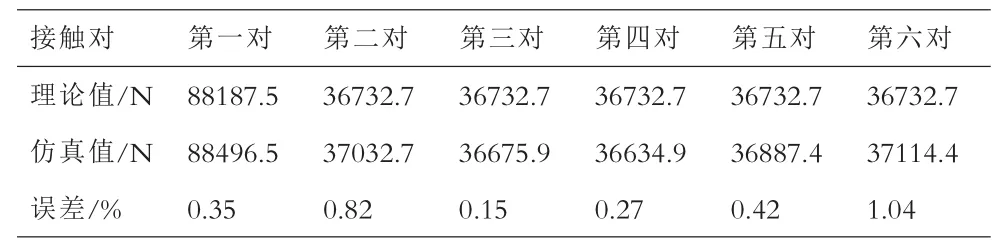
表2 理论啮合力与仿真啮合力对比

由表2可以看出仿真值与理论值很接近，最大的误差仅有1.19%，最小的误差是0.018%，说明了多刚体模型建立的正确，接触参数设置的合理。

3 结语

本文将谐波齿轮系统导入到RecurDyn中，建立多刚体仿真模型并进行接触参数的设置，对多刚体谐波齿轮系统进行动力学分析，将部件的转速以及齿轮副的啮合力与理论值进行比较，验证多刚体模型建立的是否正确以及结果的合理性。

[1]龙凯，程颖.齿轮啮合力仿真计算的参数选取研究[J].计算机仿真，2002，（6）.

[2]华顺刚，余国权，苏铁明.基于ADAMS的减速器虚拟样机建模及动力学仿真[J];机械设计与研究，2006，（6）.