用样条函数设计道路平面曲线

闫红梅,孙常春,隋 英,高兴燕

(沈阳建筑大学理学院,辽宁沈阳 110168)

用样条函数设计道路平面曲线

闫红梅,孙常春,隋 英,高兴燕

(沈阳建筑大学理学院,辽宁沈阳 110168)

提出了使用样条函数来设计道路平面曲线的方法,使所设计的平面曲线既通过给定的控制点,又能满足设计规范对曲线曲率半径的要求·

样条函数;道路平面曲线;设计

1 问题的提出

目前在我国道路的平面曲线设计中,当设计路线需要通过某些控制点时,在直线段,是通过调整线路走向来满足设计要求;在曲线段,主要是靠调整曲线半径来达到设计要求的[1]·这种设计方法,在地形地貌受到限制时,设计标准必然会降低,设计结果不能较好地满足要求·本文采用样条函数来设计道路平面曲线,很好地解决了上述问题·

2 数学模型

假设平面曲线必须通过N个控制点(x1,y1),(x2,y2),…,(xN,yN),为了保证美观,且使汽车行驶时前轮转角的变化率连续、行车顺畅,平面曲线必须光滑并有连续的二阶导数·因此,该平面曲线函数f(x)必须满足以下条件:

(1)在控制点处,f(xi)=yi(i=1,2,…,N);

(2)f(x)在区间[x1,xN]上有连续的二阶导数;

(3)平面曲线的两个端点与直线段连接,故有f″(x1)=f″(xN)=0;

(4)平面曲线各点的曲率半径应符合规范要求·

此问题属于插值问题·为了增加数值稳定性和减少舍入误差,本文采用常用的三次样条函数来构造曲线函数f(x)·

3 样条插值

3.1 三次样条函数

在[x1,xN]的任意一个小区间[xi-1,xi]上,三次样条函数是关于(x-xi-1)的分段三次多项式:

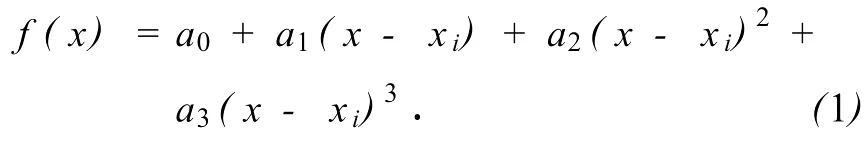
此函数有连续的二阶导数·

3.2 计算方法[2]

下面根据平面曲线函数f(x)必须满足的条件,来求解三次样条函数·

由于f(x)是分段三次多项式,故其二阶导数为分段一次多项式·在区间[xi-1,xi]上,对f″(x)的表达式分别令x=xi,x=xi-1,求得系数

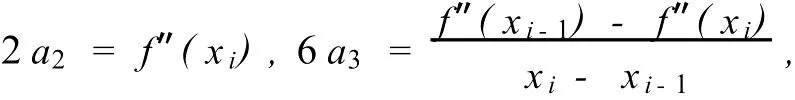
代入到f″(x)的表达式中,有

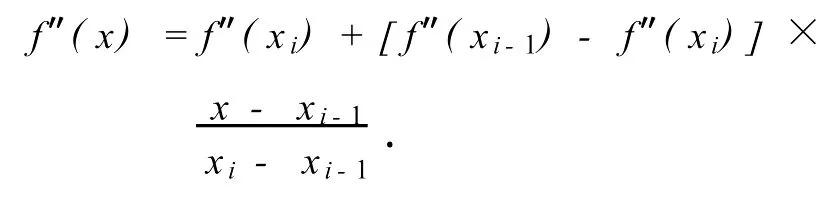
设hi-1=xi-xi-1,f″(xi)=Mi,Mi为待定系数,则有

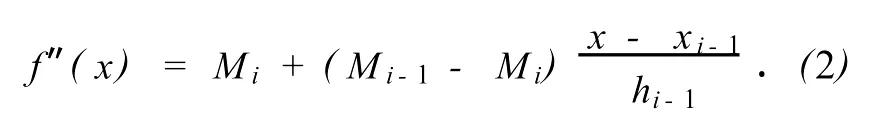
对式(2)积分两次,并以f(xi-1)=yi-1,f(xi)=yi为初始条件,以确定积分常数,得

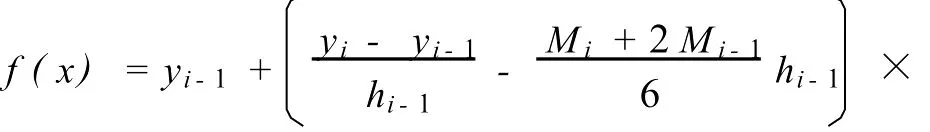
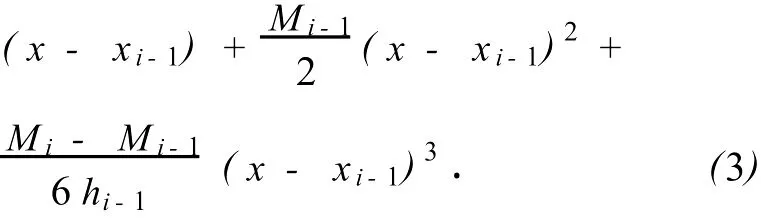
式(3)即三次样条函数f(x)在[xi-1,xi]上的表达式,对之微分,得

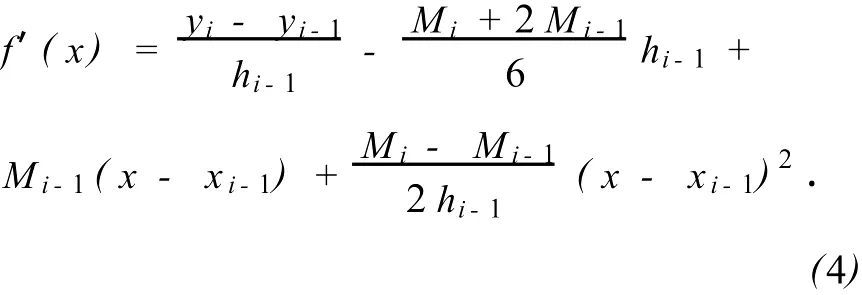
由式(4),函数f(x)在x=xi处的左导数和在x=xi-1处的右导数分别为

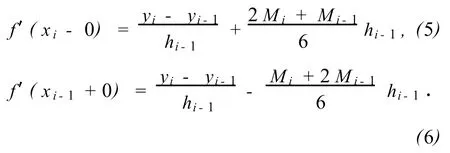
由式(6),在区间[xi,xi+1]上可以得到f(x)在x=xi处的右导数为

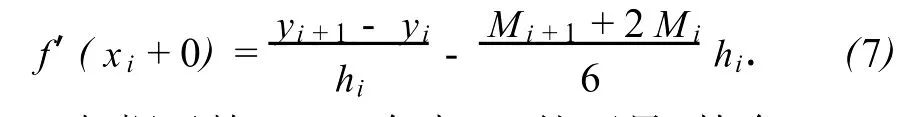
根据函数f(x)在点xi处可导,故有f′(xi-0)=f′(xi+0),即

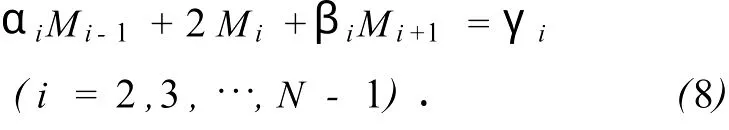
在x2,x3,…,xN-1共N-2个中间点处,得到如式(8)所示的N-2个线性方程,再加上由两个边界条件f″(x1)=f″(xN)=0可得M1=MN=0,共得N个线性方程,可以解得N个未知数M1,M2,…,MN,将之代回式(3),即得分段三次样条函数[3]f(x)·

3.3 结果分析

得到分段三次样条函数f(x)后,需要按式(9)验算f(x)在[xi-1,xi]上各点的曲率半径[4]ρ是否满足要求:

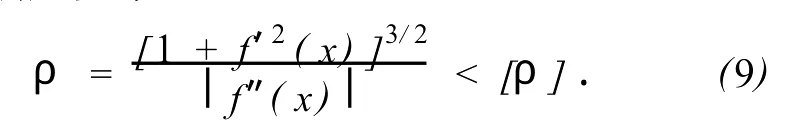
式中,[ρ]为设计规范给定的最小曲率半径·

4 算 例

某道路曲线段控制点坐标如图1和表1所示,按上述方法,由式(8)可以得方程组[5]:

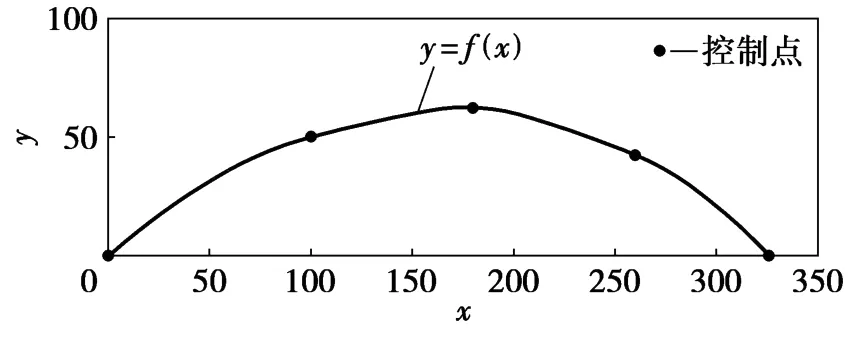
图1 道路曲线

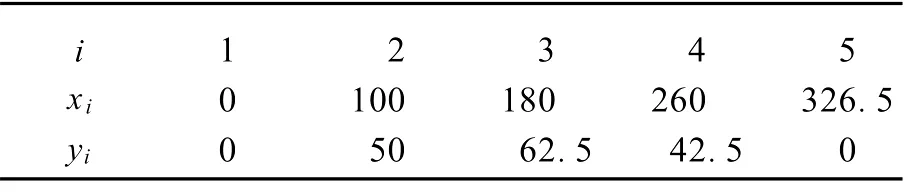
表1 控制点坐标m

将已知条件M1=M5=0代入,求解之,得

M2=-4.665 7×10-3,M3=-4.785 4×10-3,M4=-6.661 3×10-3·

将M1～M5代入式(3),整理得到f(x)的表达式如下:

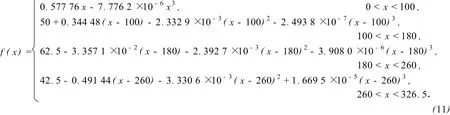
利用曲率半径公式,通过计算,f(x)在4个区间上曲率半径的最小值分别为254 m,209 m,191 m,208 m,均大于规范要求的[ρ]=60 m,符合要求·

5 结 论

利用三次样条函数来构造道路平面曲线,可以很好地满足二阶导数连续、曲率半径大于许用值等设计规范要求,且汽车行驶时前轮转角的变化率连续,保证了行车顺畅,值得推广·

[1]方绪华.道路曲线半径拟合的计算方法[J].华东公路,2000(3):48-49.

[2]孙志忠,袁慰平,闻震初,等.数值分析[M].南京:东南大学出版社,1992:188-194.

[3]张晓波.三次样条曲线在道路线形设计中的应用[J].铁道勘测与设计,2007(1):16.

[4]同济大学数学系.高等数学[M].北京:高等教育出版社,2007:173-174.

Design of Plane Curves for Road Based on Spline Function

YAN Hongmei,SUN Changchun,SUI Ying,GAO Xingyan
(School of Science,Shenyang Jianzhu University,Shenyang 110168,China)

By using spline function,the approach of designing plane curves for road is presented.The designed plane curves pass through given reference points and satisfy the request of design criterion for curvature radii of curves.

spline function;plane curves for road;design

U 412.32

A

1008-9225(2011)01-0001-03

【责任编辑:刘乃义】

2010-10-22

闫红梅(1966-),女,辽宁大连人,沈阳建筑大学讲师,硕士·