高浓漂白塔底稀释区旋转喷射管数值模拟
曾劲松 陈克复 李 军
(1.华南理工大学制浆造纸工程国家重点实验室,广东广州,510640;2.广东省造纸技术与装备公共实验室,广东广州,510640)
高浓漂白塔底稀释区旋转喷射管数值模拟
曾劲松 陈克复 李 军
(1.华南理工大学制浆造纸工程国家重点实验室,广东广州,510640;2.广东省造纸技术与装备公共实验室,广东广州,510640)
通过 Fluent的 Realizableκ-ε湍流模型以及多重旋转坐标系 (MRF)技巧,对高浓漂白塔底稀释区旋转的直形和纺锤形两种喷射管进行了正反向几种转速的数值模拟,并对其各个出口的核心速度进行了采集和分析,然后利用粒子图像测速仪 (PI V)对该模型进行了验证。结果表明,直形喷射管反向旋转转速 10 r/min左右时,其各个出口的速度差值较小;纺锤形喷射管在正向旋转转速50 r/min下,其各个出口的速度差值最小;低转速的旋转喷射管在这两种条件下均可以视为等速喷射。用 Realizable κ-ε湍流模型以及MRF技巧对旋转喷射水管进行数值计算和分析是可靠的。
Realizableκ-ε湍流;喷射;PI V;漂白塔
高浓漂白由于具有化学传质效率高、消耗蒸汽少等优点,已在造纸工业中被广泛采纳[1]。然而,由于高浓浆料流动性差,其漂白反应后浆料的输出方式直接影响到消耗能量的多少和占用空间的大小,因此,研究高浓浆料降流漂白塔塔底卸料系统的卸料器输送浆料的特征对于节约能源和节省空间、以及对卸料器的设计和改进,具有重要的现实意义。
现在的高浓降流漂白塔有Metso和 Andridz等公司采用的十字形或者一字形卸料器结合螺旋输送机等方法对高浓浆料进行卸料,但是从塔内出来的浆料仍然是高浓浆料,因此需要配备稀释单元,增加了设备的高度,缺乏设备布置的灵活性。在前期的工作中[2],利用尾流研制的卸料器在塔底设有稀释区,进入稀释区的高浓浆料首先在主喷射管的作用下完成等浓度喷射,变成了浓度为 3%~4%左右的稀浆料,为了对浆料的浓度进行小范围调整和避免旋转轴周围浆料的絮聚,增加等速喷射管,从而在稀释区各点注入等流量的水,使旋转轴周围的浆料浓度变得低一些,从而能够顺利排出。在工业生产中,简单的喷射管很多,有直形、纺锤形、腰形等。每一种喷射管都有其流场特点,虽然可以通过做大量的实验测量在不同转速下喷射管口的速度分布,但是这种方法不经济、工作量较大、流场分布信息欠缺,而且只要操作参数稍有变化,就需要重做实验进行测量,以便知道哪一种喷射器在何种转速下更适于做等速喷射。如果采用计算机流体力学 (CFD)软件对喷射管进行数值模拟计算,就可以很方便的了解喷射管的速度分布情况和其流场特点。
本实验采用 Fluent(CFD软件之一,可用于流体分析和计算)对两种低转速旋转喷射管的射流进行了数值分析和计算。
1 速度分析
根据卸料系统的要求,对喷射管的要求如图 1所示,水从中心进入,并绕中心旋转的喷射管从两侧反对称的喷口喷出,喷口的间距相等。每个喷口离中心的距离不一样,液体在输送过程中所受的管路损失阻力也不一样,所以将会造成射流喷出的速度不一样,很难形成等速喷射。
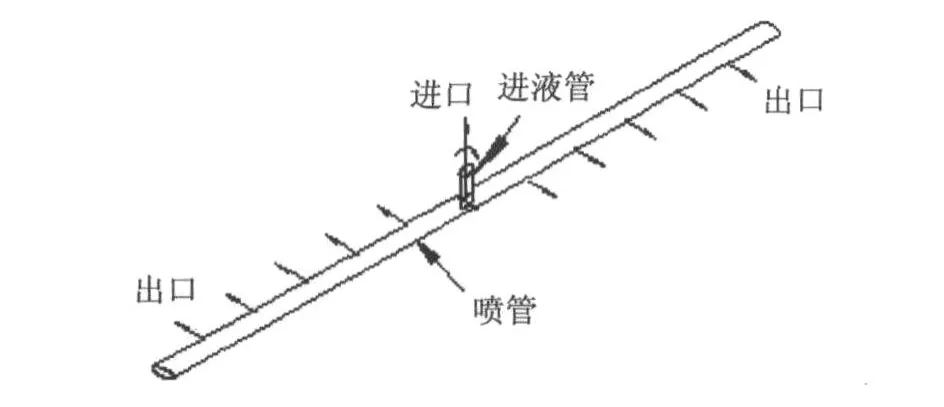
图1 直形喷射管的模型
首先对直形喷射管进行速度分析。如果出口的绝对速度为Vt,每一个出口的速度除了进口的速度 Vin引起的速度分配 Vei以外,还有旋转运动引起的离心速度 Vr。r为每个出口到中心的距离。
每个出口的矢量速度为:

旋转方向如图 1所示时,出口速度为:

旋转方向与图 1所示方向相反时,出口速度为

从上面的速度分析可以看出,正向和反向旋转时,出口速度完全不同,所以为了实现等速喷射,必须对其正向和反向旋转的情况都要进行研究。
2 建模和网格划分
为了研究喷射管的流场,对比较常用的直形喷射管和纺锤形喷射管进行模拟。如图 1所示,直形喷射管的长度为 300 mm,进口直径为7 mm,出口直径为3 mm。进口在喷射管的中心,两侧出口对称地离中心的距离分别为 25 mm、50 mm、75 mm、100 mm、125 mm。纺锤形喷射管如图 2所示,其长度和进出口直径、进出口位置与直形喷射管一样。不同的是相邻出口处所在的截面直径关系为=8 mm,随着离开中心距离的增大,喷射管直径呈递减趋势。

图2 纺锤形喷射管的模型
利用 UG(EDS公司开发的 CAD/CAM/CAE软件,可用于三维绘图)对直形和纺锤形喷射管进行几何建模后,采用 ICEM(CFD软件之一,用于划分网格)对几何模型进行网格划分。
3 数值计算方程和边界条件
3.1 数值计算方程
在流体动力学中将从喷射管进入静止或运动速度比较慢的流体中的射流都可视为自由湍流[3],所以在 CFD求解计算过程中湍流模型采用 Realizableκ-ε模型,这种双方程模型适合的流动类型比较广,包括有旋均匀剪切流、自由流 (射流和混合层)、腔道流动和边界层流动。对以上流动过程的模拟结果都比标准κ-ε模型的结果好[4]。有限体积法 (FVM)求解方法采用了 Fluent的求解压力耦合方程组的半隐式方法 (SI MPLE)算法,这种算法是目前工程上应用最为广泛的一种流场计算方法。计算通量采用二阶迎风形式。没有传热过程,所以数值计算中采用的守恒方程和κ-ε方程如下[4]:
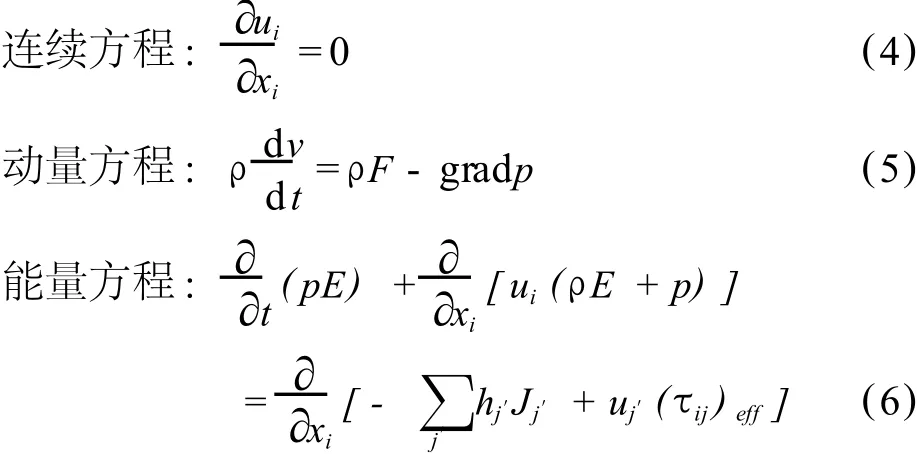
其中:F是单位质量流体的质量力;gradp为流体内应力张量的梯度;p是流体内应力张量的分量 ;Jj′是组分 j′的扩散通量 ;hj′是组分j′的焓值; τij是应力张量 。
而 Realizableκ-ε模型的湍动能及其耗散率输运方程为:
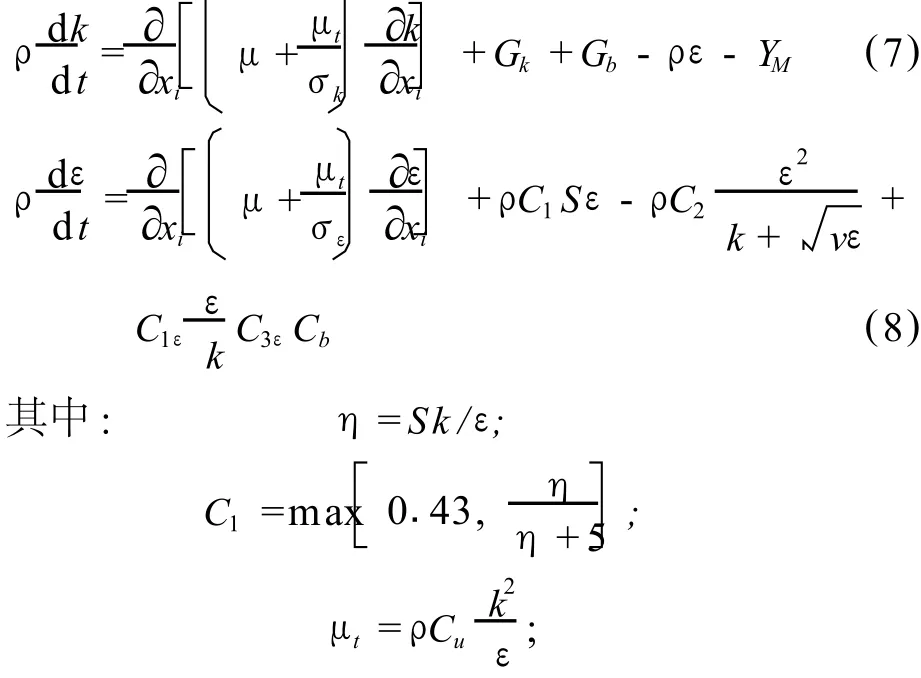
C1ε=1.44,C2=1.9,σk=1.0,σε=1.2;
Gk表示由于平均速度梯度引起的湍动能产生;Gb表示由于浮力影响引起的湍动能产生;
YM表示可压缩湍流脉动膨胀对总的耗散率的影响;
C1ε、C2是常数;
σk和σε分别是湍动能及其耗散率的湍流普朗特数。
3.2 边界条件
流体为水,进口速度为 6 m/s,方向为竖直向下,喷射管的 10个出口为压力出口,压力为 0,采用moving reference frame(MRF)方法进行求解,水射流均从喷射管的水平方向射出。转速变化范围为0~90 r/min,旋转方向分为正反两个方向,分别在FluentV6(Fluent软件的版本)中进行模拟。
4 结果与讨论
为了研究在低转速下直形和纺锤形喷射管的近似等速区,在 FluentV6中分别对其进行了数值计算,对不同转速下各个出口的速度矢量的输出数据进行了采集。由于喷射管喷出的水为射流,本实验主要研究其速度核心区,也就是最大速度区域。射流稳定后,由喷口边界起向内外扩展的紊动掺混部分为紊流剪切层混合区;中心未掺混部分保持原出口流速,成为速度核心区。速度核心区的流速始终保持不变并等于喷口处射流的最大速度[3]。所以,喷射管每个出口的核心速度大致相等,就可以保证近似等速喷射。
4.1 直形喷射管
直形喷射管的出口速度分布见图 3。从图 3中可以看出,对于直形喷射管的各个出口速度分布的情况,速度分布连续,所以在不同的转速 0~90 r/min下,可以选取输出数据中的最大速度矢量来进行分析和研究[5-7]。
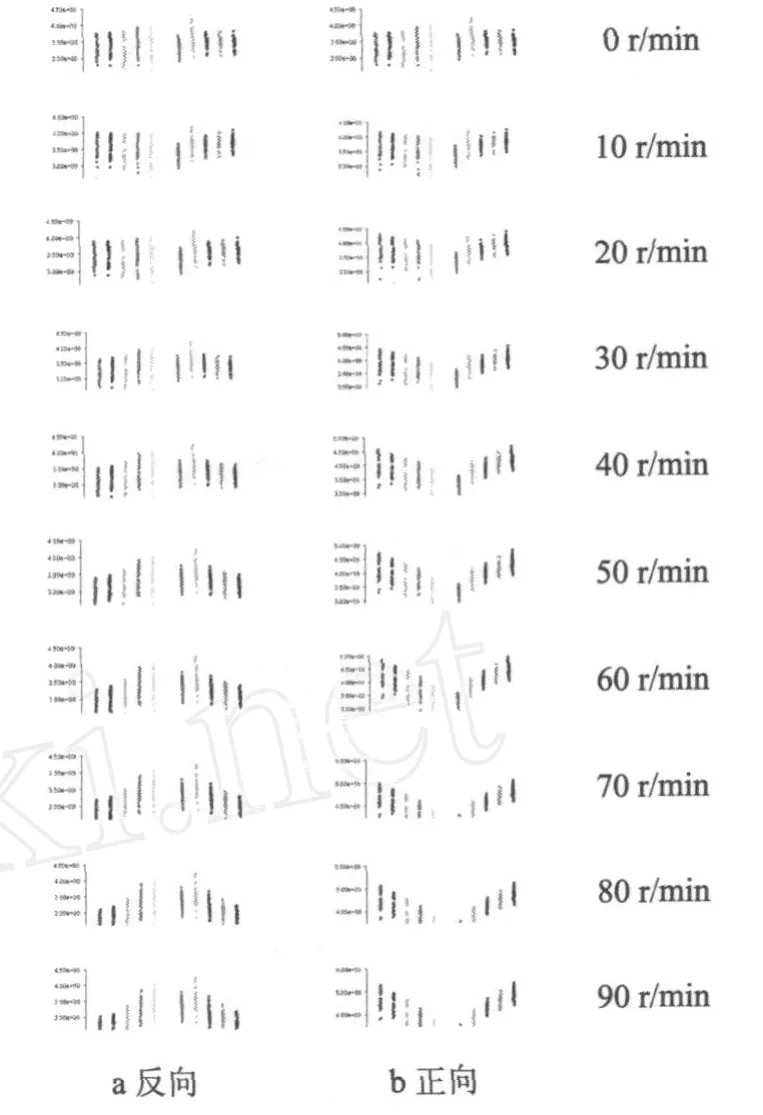
图3 直形喷射管的出口速度分布
如图 3所示,直形喷射管绕回转中心旋转产生的离心速度方向与出口方向一致为正向,其速度矢量表达式如式 (2)所示;反之为负向,其速度矢量表达式如式 (3)所示。从图 3中可以看到,直形喷射管在反向过程中,随着转速的升高,中间的出口速度变化不大,但是两侧出口的速度在不断降低;在正向过程中,中间的出口速度变化依然不大,但是两侧的出口速度在不断增加。出口位置从左到右分别为出口1、2、3、4、5、6、7、8、9、10。从 Fluent的出口最大速度矢量输出数据,分别利用Matlab软件 (矩阵实验室 Matrix Laboratory的简称,是美国 Math-Works公司出品的商业数学软件,用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境)绘出三维图 4和图 5[8-9]。
从图 4和图 5中可以知道,不管是正向还是反向,中间出口 4、5、6的速度在不同转速下变化不大,但是这 3个出口的速度彼此相差较大。喷射管在不同转速下,其出口速度分布大致相同。喷射管两侧的速度在不同的出口和不同的转向、转速下,变化不一。如图 4所示,直形喷射管在反向旋转时,随着转速的增加,出口 1、2、3、7、8、9的速度越来越小;在低转速时,各个出口的速度大小相差小一些;转速越高,各个出口的速度大小相差得越多。如图 5所示,直形喷射管在正向旋转时随着转速的增加,出口1、2、3、7、8、9的速度越来越大;在低转速时,各个出口的速度大小相差小一些;转速越高,各个出口的速度大小相差得越多。通过比较,反向时低转速下各个出口速度相差更加小,特别是在转速 0~10 r/min之间时,其速度差为 0.2 m/s左右。这种现象可以从式 (2)和式 (3)中得到解释,速度分量中的离心速度 Vr=2πnr不仅与转速有关,而且与回转半径有关,对于中间的出口由于回转半径小,所以在不同转速下,其离心速度变化不会太大。在正向旋转时,离心速度分量成为增加的速度分量;在反向旋转时,离心速度分量成为减少的速度分量。
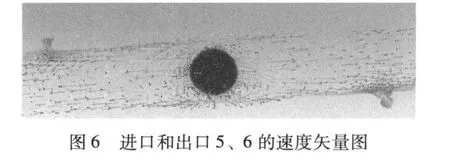
同时,从图 6和图 7的速度矢量图看出,出口速度不仅受上面叙述的离心速度 Vr的影响,还受进口速度引起的分配速度 Vei的影响,特别是离中心较近的出口速度受影响最大,而离中心较远的出口受回流的影响较大。同时,在管内有少许的二次流。在图 7中,出口 9、10离进口较远,受进口速度影响较小,但是主要受离心速度的影响。在这两个口中有较多量的二次流出现[10-14]。



4.2 纺锤形喷射管
在 FluentV6中对转速在 0~90 r/min时纺锤形喷射管的进、出口速度进行了模拟,如图 8所示。
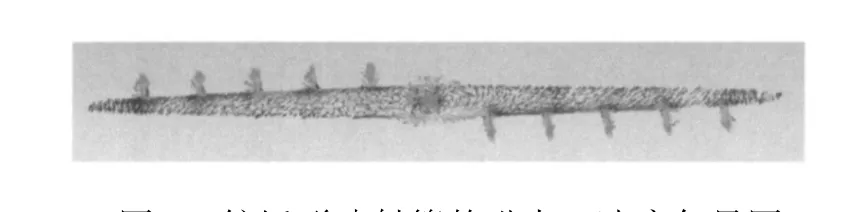
图8 纺锤形喷射管的进出口速度矢量图
由于模拟、分析方法同直形喷射管,所以这里只选取部分速度模拟分布图进行分析。通过分析比较发现,纺锤形喷射管在正向旋转 30~70 r/min之间,特别是在 50 r/min左右,速度大小比较接近,其最大与最小速度差值达到 0.3 m/s,而且在每个出口的速度分布比较均匀,如图 9所示。
5 PIV实验
为了验证上面的模型以及相关分析是否可靠,采用 PI V系统对喷射管在各种转速下出口的喷射速度进行验证。实验时采用丹麦丹迪公司 (Dantec Dynamics A/S)现代的粒子图像速度仪 PI V进行速度测量。PI V系统由二维 PI V图像记录系统、分辨率为 2048×2048的 CCD照相机以及 135 mJ双腔脉冲 PI V激光器组成。测量原理图如图 10所示,CCD照相机和 PI V激光器垂直放置[13]。如果要测量喷射管另外一侧的速度,就需要重新调整 CCD照相机和 PI V激光器。实验中水的示踪粒子为聚酰胺粒子,密度为1.0×103kg/m3。

图9 纺锤形正向旋转时喷射管的进、出口速度分布
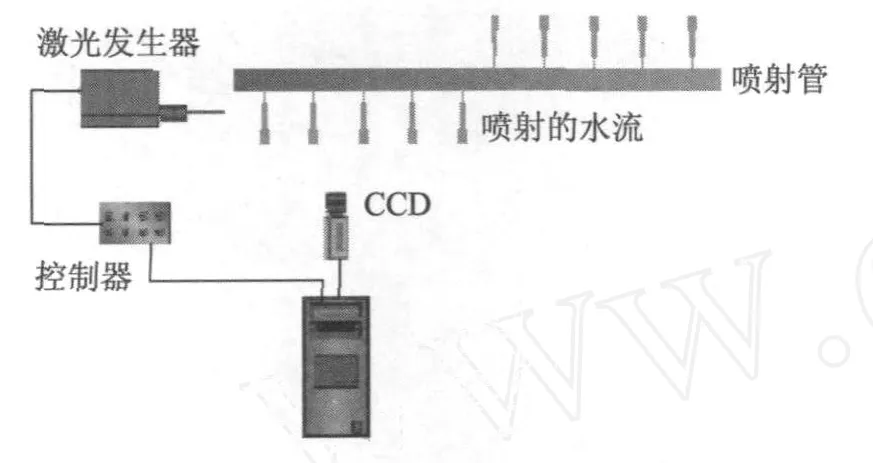
图10 PI V系统安装
实验发现,速度的模拟值与实验值变化趋势相同,如图 11所示,直形喷射管在转速为 0~90 r/min进行反向旋转时,出口 1、2、3、4、5的速度模拟值与实验值相差大约在 12%左右。同时对直形喷射管在其他出口和正向旋转,以及纺锤形喷射管进行同样的实验,也有相同的验证效果。所以,模拟计算的模型和数值分析是可行的。
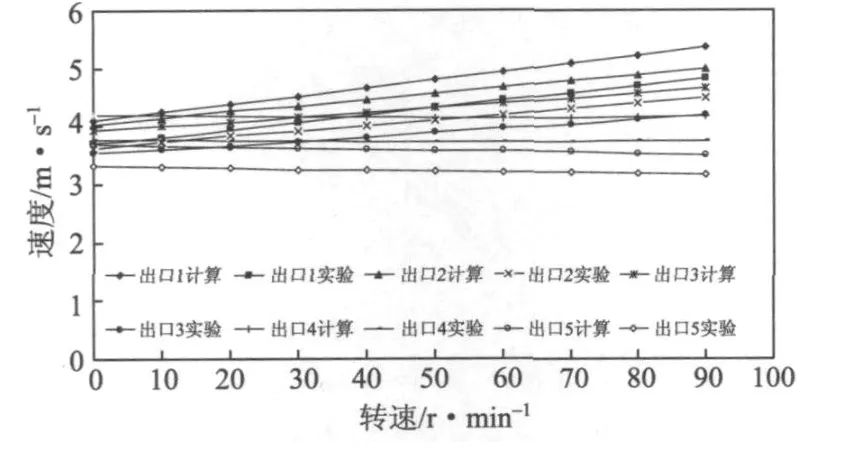
图11 PI V实验和数值计算的速度
6 结 论
直形喷射管或纺锤形喷射管在塔底对稀纸浆进行进一步喷射稀释,就要求在一定转速下喷射管的各个出口速度差值比较小,形成近似等速喷射,从而使旋转轴周围的稀纸浆不易絮集。通过对这两种喷射管的数值模拟以及粒子图像测速仪 (PI V)验证,得出了结论。
6.1 喷射管几何特性呈反对称,其速度矢量也大致对称,但是速度大小不相等。这是由于管内的二次流动造成的。
6.2 直形喷射管要形成近似等速喷射,可以采用反向旋转,转速调整到 10 r/min左右进行。
6.3 纺锤形喷射管要形成近似等速喷射,可以采用正向旋转 50 r/min左右。
6.4 旋转低速射流采用 Fluen的 Realizableκ-ε模型和多重旋转坐标系 (MRF)技巧进行分析计算是可行的。
[1] 陈克复.制浆造纸机械与设备 (下)[M].北京:中国轻工业出版社,2009.
[2] Zeng J L,Chen K F,LiJun.CFD simulation of dischargers'dilutionzone in high consistency bleaching tower[C]//The 4thInternational Symposium on Emerging Technologies of Pulping and Papermaking,Guangzhou,2010.
[3] 休斯 W F,布赖顿 J A.流体动力学 [M].北京:科学出版社,2002.
[4] 江 帆,等.Fluent高级应用与实例分析 [M].北京:清华大学出版社,2008.
[5] OlyaeiA,Green S I.Three-dimensional geometry and flow field modeling of forming fabrics[J].Nordic Pulp and PaperResearch Journal,2009,24(3):342.
[6] Prajapati P,Mozaffari F E.CFD Investigation of the Mixing of Yield-Pseudoplastic Fluids with Anchor I mpellers[J].Chem.Eng.Technol.,2009,32(8):1211.
[7] Asteriadou K,Hasting A P.Exploring CFD Solutions for Coexisting Flow Regimes in a T-Piece[J].Chem.Eng.Technol.,2009,32(6):948.
[8] 陈怀琛.Matlab及其在理工课程中的应用指南[M].西安:西安电子科技大学出版社,2002.
[9] 肖劲松,王沫然.MATLAB与科学计算[M].北京:清华大学出版社,2000.
[10] 陈克复.造纸机湿部浆料-流体动力学[M].北京:轻工业出版社,1984.
[11] 刘树红,吴玉林.应用流体力学 [M].北京:清华大学出版社,2006.
[12] 张兆顺,崔桂香,许春晓.湍流理论与模拟[M].北京:清华大学出版社,2005.
[13] 丹迪粒子图像测速仪Dantec PI V[S].香港麦迪技术有限公司.
[14] 杨 旭,陈克复.流浆箱稀释水调节原理及特点初探[J].中国造纸,2010,29(5):17.
[15] 狄宏伟,孙德文,宋宝祥.滑石颜料高剪切流变性能的研究[J].中国造纸,2010,29(8):1.
(责任编辑:马 忻)
Numerical Si mulation of Rotating Spray Tube with Low Speed
ZENG Jin-song*CHEN Ke-fu L IJun
(1.State Key Lab of Pulp and Paper Engineering,South China University of Technology,Guangzhou,Guangdong Province,510640;2.Public Lab of Paper Technology and Equipment,Guangzhou,Guangdong Province,510640)
( * E-mail:zjs789zjs@126.com)
Based on Realizable κ-ε turbulent model and MRF technique in Fluent,the two kinds of rotary spray tube such as straight and spindle ones were simulated under different for ward and reverse rotating velocities,and the core velocities of each outlet were collected and analyzed.Then PI V system was used to validate the model.The results showed that the outflow velocity difference of the straight-type spray line is the smallest when the angular velocity is about10 r/min with the reverse rotation.While for the spindle spray line,the outflow velocity difference is smallest when the angular velocity is about50 r/min with the forward rotation.The sprays of rotary spray tube under low rotation speed can be considered as the constant velocity sprays in these two conditions.The numerical simulation results agreed with the PI V experiment data.So both Realizable κ-ε turbulent model and MRF technique are reliable and the calculated results are correct.
Realizable κ-ε;spray;PI V
TS733+.5
A
0254-508X(2011)04-0006-05
曾劲松女士,在读博士研究生;主要研究方向:纸浆与造纸装备技术。
2010-12-06(修改稿)
本课题为 “十一五”国家自然科学基金重点支持项目,项目名称“林业一体化工程技术研究与示范”,课题任务书编号为2006BAD32B06-2。

