山体环境对建筑屋面风压影响的数值模拟

高志飞,彭兴黔,崔利民,珠海

(华侨大学土木工程学院,福建泉州 362021)

山体环境对建筑屋面风压影响的数值模拟

高志飞,彭兴黔,崔利民,珠海

(华侨大学土木工程学院,福建泉州 362021)

基于计算流体动力学软件ANSYSCFX,采用剪切应力传输(SST)k-ω湍流物理模型和非结构化网格,对山体环境下低矮民房中较为典型的二层双坡屋面房屋进行数值模拟.在山体环境影响下,分析房屋表面风压随山体高度变化、不同坐落位置和各风向角下的分布规律.结果表明,山体对房屋的影响,屋面的体型系数与平坦地区差异较明显,且与山体高度、山坡度和建筑的坐落位置有关.山体高度的变化对屋盖结构体型系数的影响较小,而房屋的坐落位置影响最为明显.

山体;低矮民房;风压;数值模拟;体形系数

气流经过山地丘陵地区时,复杂的地形、地貌将显著改变近地流动风速、风压和湍流结构,使得这些地区的风流场呈现与平坦地区较明显的差异[1].即风速和风压的分布很不规则,且由于山体的相互影响,山上建筑结构表面风压分布更为复杂.对于山区建筑,GB 50009-2001《建筑结构荷载规范》在考虑地形影响的风压增大系数时,采用山体或山坡模型相关公式并用线性插值法对风压进行修正;但是,对于山地建筑体形系数的相关规定,也仅有建筑坐落于山脚时,在一定范围内的体形系数的规定[2].然而,这些规定很不完善,当气流沿山坡运动时,随着建筑坐落于山上不同高度处,其体形系数也出现复杂多变.近年来,通过对多次台风灾害的调查和分析发现,山地丘陵地区建筑的受灾害程度与其所处的地理位置直接相关.主要原因是,在一些特殊地形和风向的情况下,会形成局部风力增强的效应,进而增大台风对低矮房屋的破坏力.本文采用数值模拟的方法,对山体工况下的建筑实体模型的表面风荷载体型系数变化进行分析.

1 计算域的设置及网格划分

1.1 计算域的设置

对于山体地形,数值风洞模型复杂且体形比较大,阻塞率对其计算结果影响较大.因此,设置一个较大计算域,如图1所示.图1中:L1为计算域上游长度(0°风向角下流域入口到坐标原点的距离);L2为计算域下游长度(0°风向角下流域出口到坐标原点的距离);B为计算域宽度;Hm为计算域高度.坐标原点(0,0,0)设置在山丘模型中心,L1取8L,L2取14L,B取28L,Hm取8L.其中:L为山的截面参数(m).所有数值风洞设置均满足阻塞度小于5%的要求[3].

1.2 网格的划分

为适应低矮建筑的体型要求,采用计算流体力学软件ANSYS CFX模拟区域内风的流动特性,并通过对实体(地面或建筑物)表面加密网格的方法来得到较精密的网格,如图2所示.由图2可看出,模型附近的网格尺寸小,网格最小尺寸为2 m,分布密集;而远离模型的地方网格较大,最大尺寸为60 m,分布较疏.采用具有良好适应性的四面体网格离散单元,每种工况产生220万左右的四面体单元.

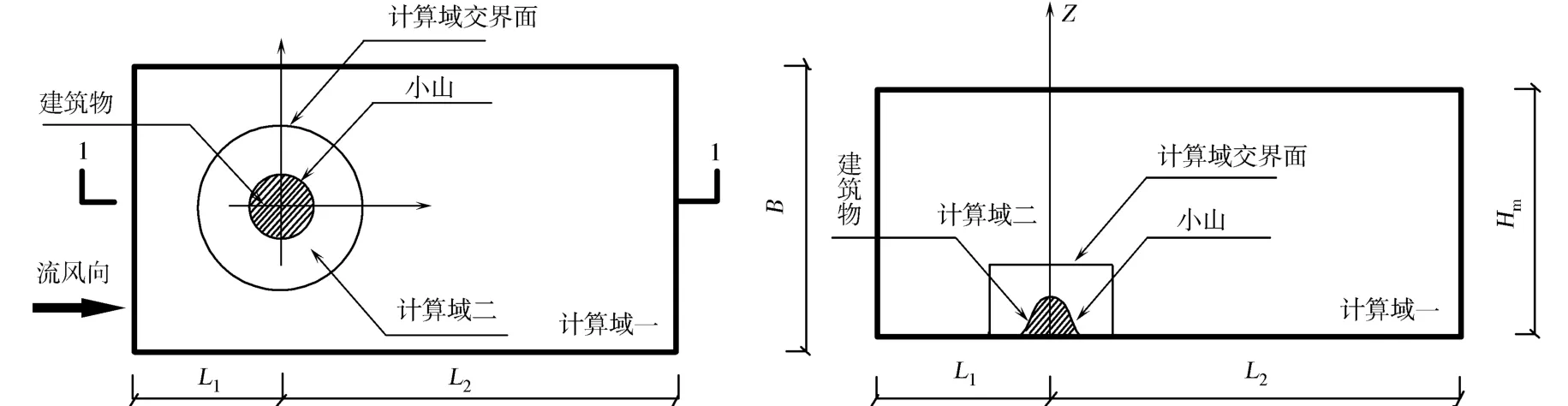
图1 计算域构成平面Fig.1 Plane of Computational domains

图2 网格划分图Fig.2 Grid division

为了最大程度地与实际情况相符,采用1∶1足尺寸模拟,将建房处的山局部削平,并在其上建房.山体位置Z由正弦曲线式控制[4],有

式(1)中:H为山体的高度;L为山的截面参数.设置H/L参数为1/2,房屋分别坐落在0.1H～1.0H处,以Z=0.1H表示.

选取低矮民房中较为典型的二层双坡屋面房屋作为房屋模型,其长度方向为12 m,宽度方向为8 m,檐口高为7 m,屋面坡度为30°.山模型、房屋与山的相对位置及房屋尺寸,如图3,4所示.

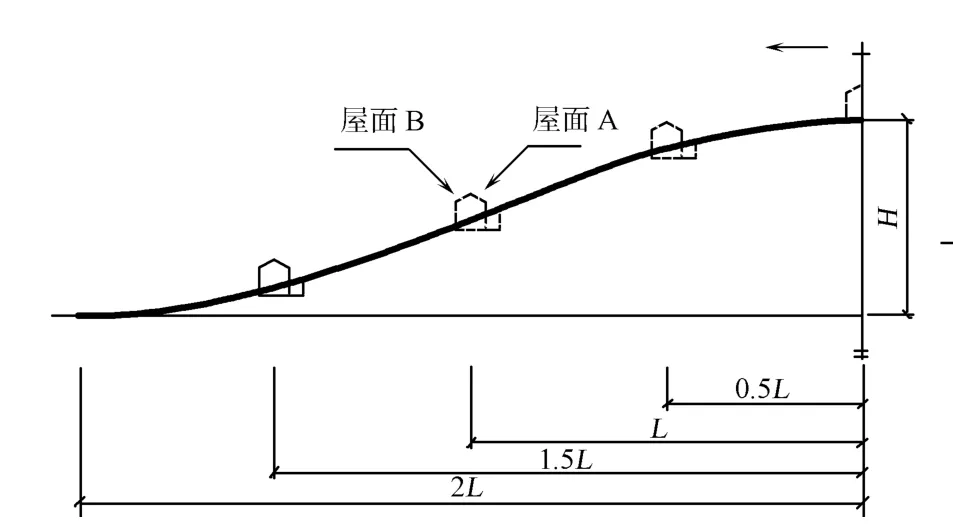
图3 山体上房屋相对位置Fig.3 Relative position of the house on the mountain

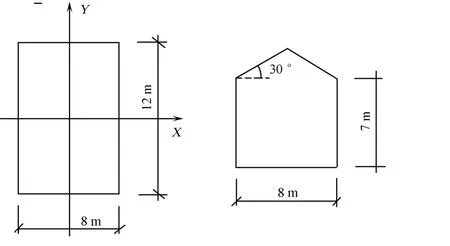
图4 房屋几何尺寸(单位:m)Fig.4 Size of the house(unit:m)

2 控制方程的选择和边界条件

2.1 控制方程的选择

采用由湍流模型封闭控制方程进行求解的时均模拟方法,其气流流动控制方程[5]的通用形式为

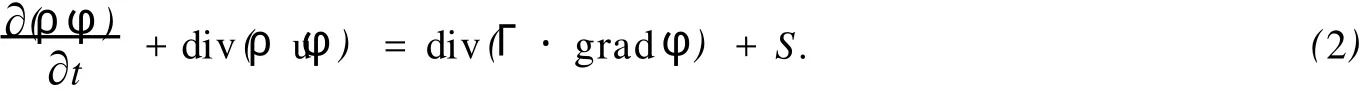
式(2)中:各项依次为瞬态项、对流项、扩散项和源项;ρ为空气的质量密度;u为速度矢量;φ为通用变量;Γ为广义扩散系数;S为广义源项.湍流模型采用目前被业界广泛认同的剪切应力输运模型(SSTk-ω模型)[6].

2.2 边界条件的选择

选用入口边界条件,取=×(Z/Zb)α.当地面粗糙度指数α为0.16时,=6.97 m·s-1, Zb=1 m.入口湍流剖面按湍动能k(Z)和耗散率ε(Z)的形式输入的表达式[7]为

式(3)中:系数Cμ=0.09;γ=1.2;β=1;K=0.4;按文献[8]的经验式,湍流积分尺度Lu=100(Z/30)0.5;按文献[9]的经验式,湍流强度I(Z)=0.1×(Z/ZG)-α-0.05.底面采用非滑移壁面,其他侧面采用自由滑移壁面,出口采用开放式的压力出口.

为保持入口处的边界条件,在内部无扰动的空风洞中进行实验.入口处的边界条件对风场模拟的影响很大[10],距入口一段距离后,未受扰动新位置的平均风速和湍流剖面不一定与入口保持一致.在数值风洞模拟的稳态计算中,对建筑物表面平均压力起主要作用的是平均风剖面,通过修改式(3)的参数γ和β来修正湍流风剖面,重点保证平均风剖面在流场中不变.

3 计算结果及分析

风荷载体型系数(μs)是,将各计算点的风压系数Cp,i按该点所属面积A i作加权平均后得到的,其计算式为

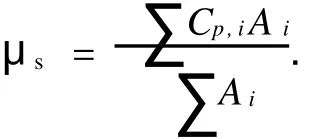
屋盖是低矮房屋的薄弱部位.在不同山体高度下,以A,B两屋盖面为研究对象,分析其表面风压随房屋坐落于山体不同位置各风向角下的分布规律,其计算结果如图5所示.

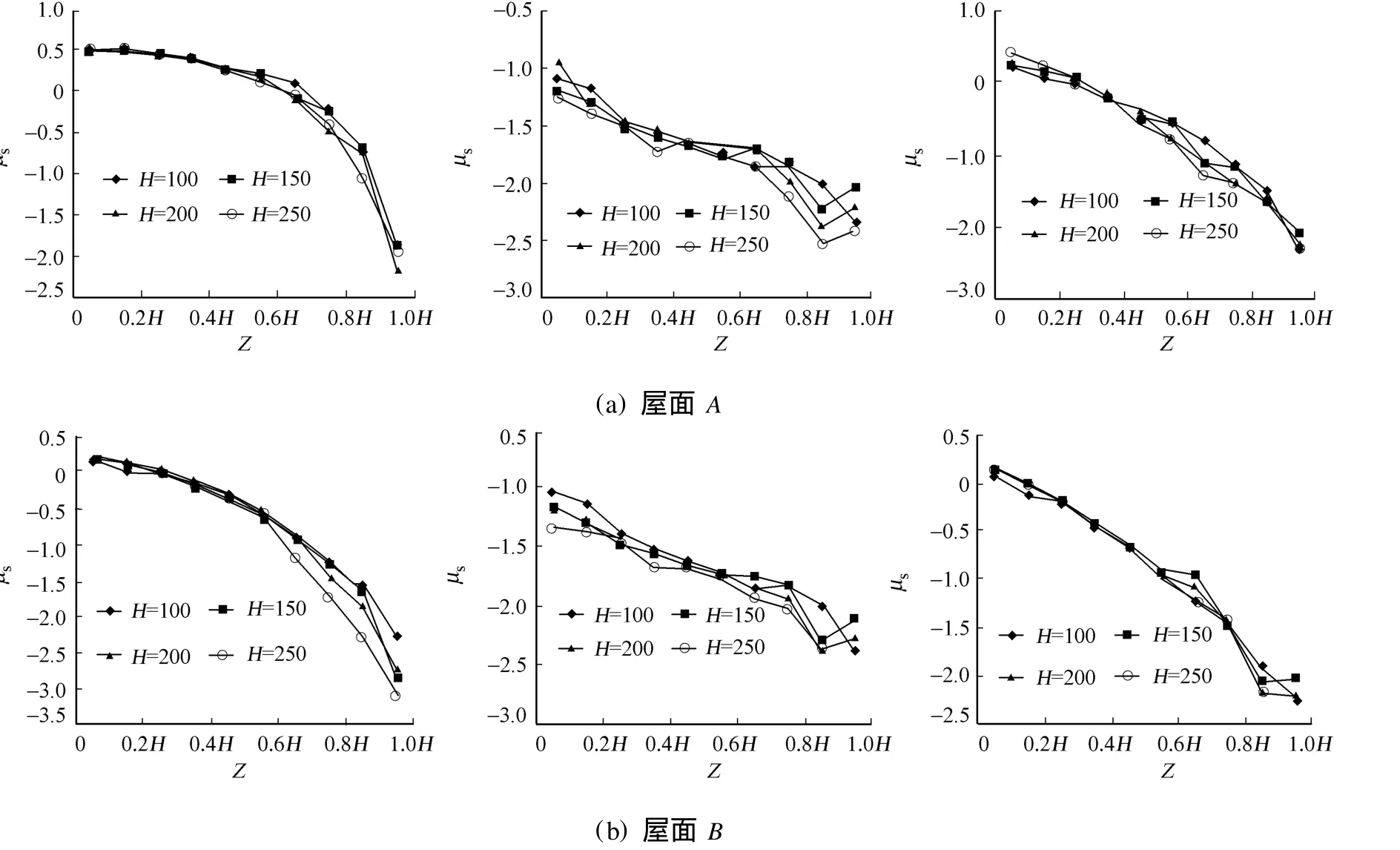
图5 屋面体型系数随坐落位置的变化曲线Fig.5 Curve of shape coefficient versus hours location

由图5可见,当H固定时,屋面A,B体型系数均随坐落位置Z的升高而降低,在山顶处受负压最大.在0°风向角下,屋面A为迎风面,屋面B为背风面.屋面A,B体型系数随Z升高而降低,由风压力渐变为风吸力.

山体的高度随坐落位置不同,其各风向角下流场如图6所示.图6中:H=150 m;箭头方向代表风流向;箭头大小代表风速大小.

从图6(a)可知,在Z″=0.1H～0.5H范围内,由于山坡度较为平缓,且屋面A,B均受过山风场影响,风压随坐落高度变化不明显,体型系数变化较为缓慢,体型系数相差不大且随山体高度变化不大,几条线几乎重合.在靠近山脚处,由于受到山体的影响,气流在屋面A上没有附着,而屋面B由于受屋檐前方涡流的影响,屋面A,B均受正压,屋面A体形系数大约为屋面B体形系数的2倍.

从图6(b)可知,在Z=0.5H到Z=1.0H范围内,随着Z的升高,山坡度增加,风速变大,体型系数变化较大,且随山体高度H增加,几条线分离.由于屋面A前方涡流逐渐减弱,气流在屋面A处的屋檐处分离,屋面A,B由受正压渐变为受负压,且屋面B前方涡流逐渐减弱变化较明显,屋面B受到的影响渐渐超过屋面A.

从图6(c)可知,靠近山顶处,山坡度变化趋于平缓而风速变化增加,山顶处风速最大,气流在屋面A的屋檐处分离更为明显,屋面A前方涡流强度最弱,屋面A,B体型系数绝对值最大,大约为山脚处体型系数绝对值4～5倍.

从图6(d)可知,在180°风向角下,屋面A,B体型系数变化情况与0°风向角下类似.此时,屋面A, B受到的不是过山风场,风速较小.所以,屋面A,B体型系数较0°下较小些,且主要受到风压随高度变化的影响,其体型系数变化接近为直线.

从图6(e)可知,在90°风向角下,房屋建于山脊上,屋面A,B为侧风面,气流在屋檐处分离.由于平均风速剖面的影响,在接近房屋的另一端处再次附着,在屋面上形成漩涡,屋面A,B类似,均受负压.由于其主要也是受风压随高度变化的影响,其体型系数变化近为直线.

从图6(f)可知,最大值出现在0.9H处而不是山顶.这是因为在山顶处,由于受山体的影响,气流仅仅在屋檐处分离,没有出现再附着,显现体型系数较0.9H处小些.最小体型系数绝对值大约为山脚处体型系数绝对值的2倍,变化趋势较为明显.

由图6可见,在0°及180°风向角下,屋面A,B体型系数在靠近山脚处随山体高度H增加,体型系数绝对值均有所增加,但增加不大;而在靠近山顶处,随着H的增加,体型系数绝对值增加较山脚明显,屋面受的风吸力增加.90°风向角下的变化最明显,是因为屋面A,B为侧风面,主要受风压随高度变化及山坡度的影响.

4 结论

以位于三维正弦山体地形下的二层双坡屋面低矮房屋为研究对象,数值模拟屋盖结构体型系数.研究结果表明,由于山体对房屋的影响,屋面的体型系数与平坦地区差异较明显,且与山的高度,山坡度和建筑的坐落位置有关系.

山体高度的变化对屋盖结构体型系数的影响较小,而房屋的坐落位置影响最为明显.特别是在山顶处,房屋处于山顶负压区,且体型系数变化很大,对抗风很不利,山体对低矮建筑风荷载的影响不容忽视.研究成果能够为工程设计人员提供相关参考,具有很强的实用价值.

[1]陈平.地形对山地丘陵风场影响的数值研究[D].杭州:浙江大学,2007.

[2]中华人民共和国建设部.GB 50009-2001建筑结构荷载规范[S].北京:中国建筑工业出版社,2006.

[3]黄本才.结构抗风分析原理及应用[M].2版.上海:同济大学出版社,2008.

[4]TETSURO T,AZUMA O,YOHEIS.LESanalysis of turbulent boundary layer over 3D steep hill covered with vegetation[J].Journal of Wind Engineering and Industrial Aerodynamics,2007,95(9/10/11):1463-1475.

[5]王福军.计算流体力学分析:CFD软件原理与应用[M].北京:清华大学出版社,2004.

[6]黄本才.下游受扰对上游施扰高层建筑的风力的影响[C]∥第十二届全国结构风工程会议论文集.西安:[s.n.], 2005:712-717.

[7]RICHARDSA PJ,HOXEYB R P,SHORT L J.W ind pressures on a 6 m cube[J].Journal of Wind Engineering and Industrial Aerodynamics,2001,89(14/15):1553-1564.

[8]KA TARZYNA K,WOJCIECH M,AGN IESZKA J K.M ulticriteria op timization of the building arrangement with application of numerical simulation[J].Building and Environment,2000,35(6):537-544.

[9]周大伟,高层建筑风压风流场稳态与大涡模拟研究[D].上海:同济大学,2005.

[10]曾凯.计算风工程的几个关键影响因素分析[C]∥第十二届全国结构风工程学术会议论文集.西安:[s.n.],2005: 743-750.

(责任编辑:钱筠英文审校:方德平)

Numerical Simulation of W ind Pressure on the Building Roof in the Mountain Environment

GAO Zhi-fei,PENG Xing-qian, CU ILi-ming,ZHU Hai
(College of Civil Engineering,Huaqiao University,Quanzhou 362021,China)

Based on computational fluid dynamics(CFD)software CFX,the shear stress transport(SST)k-ωturbulence physical model and unstructured grids,the numerical simulation is carried out for the typical low-rise two-story houses with double-sloping roof in the mountain environment.Under the influence of the mountain environment,the distribution of the roof pressure with different height of the hill,different houses locations and different w ind direction is analyzed.The results show that the roof shape coefficients are obviously different to the one in the flat region,and are relevant to the height of the hill,slope degree,houses locations.The hill height influences little the roof shape coefficients,and the location of house influences most significantly the coefficient.

mountain;low-rise houses;wind pressure;numerical simulation;shape coefficient

TU 312+.1

A

1000-5013(2011)02-0207-05

2010-03-08

彭兴黔(1959-),男,教授,主要从事钢结构抗风抗火的研究.E-mail:pxq@hqu.edu.cn.

福建省科技计划重点项目(2010Y0037);福建省自然科学基金资助项目(2009J01255);风工程与桥梁工程湖南省重点实验室开放基金资助项目(2009-01)