一种基于能量模型的曲面展开改进算法
严国彪,刘斌
(华侨大学机电及自动化学院,福建泉州 362021)
一种基于能量模型的曲面展开改进算法
严国彪,刘斌
(华侨大学机电及自动化学院,福建泉州 362021)
针对现有算法存在的问题,提出一种基于能量模型的自由曲面展开改进算法.算法的改进主要是对时间步长的调整.通过调整时间步长,避免展开过程中发散现象,同时也有效地提高曲面展开的精度,较好地解决展开过程中因迭代次数过多而引起的振荡现象,提高曲面展开的质量.算例结果表明,算法是有效的,可以满足实时交互设计的要求.
曲面展开;能量模型;时间步长;三角网格
3D曲面展开技术广泛应用于飞机、汽车、船舶,以及服装和鞋类等设计和制造领域中.这些行业都需要得到设计产品的平面外形图.传统的方法是将最初的平面外形图手工进行反复缝合、修改,直至最终得到理想的外形图.许多应用于产业的CAD/CAM系统具有将立体曲面展开为平面的功能,大大方便了后继的设计和制造.曲面的展开问题,特别是复杂曲面的展开问题[1-2],一直是计算机辅助几何设计领域研究的热点和难点.合理地展开三维曲面是CAD&CG领域中众多技术得以实现的重要基础,国内外众多学者进行了不少相关的研究.文献[3-5]在曲面展开系统中采用了弹簧-质点模型对其曲面展开进行优化,但他们研究的侧重点不同.上述算法都未考虑到迭代优化中的发散问题,即如果参数选择不合理的话,则很容易产生发散,使迭代过程不收敛,导致展开计算失败.基于此,本文提出基于能量模型曲面展开的改进方法.
1 曲面展开的能量模型
1.1 能量模型的建立
曲面展开前,先对曲面进行三角化,并由三角化网格建立一个弹簧质点系统.该系统的物理量与某些几何量是相对应的,如力、质量和弹性变形能是由网格节点间的距离和三角片的面积确定的.原始网格形状和展开后二维片形状之间的差别,可视为一种贮存在弹簧质点系统中的弹性变形能,通过释放变形能,提高曲面展开质量.由于能量是状态的单值函数,与过程无关,所以能量的关系式比较容易列出.
在能量模型中,大多数基于物理的参数,如系统力、质量和弹性变形能等,均由其相关的几何量定义而得[6-7].研究中可将材料特性加入,由此,不同的材料特性将可得到不同的展开结果,有利于工程上的实际应用.
弹簧质点系统的示意图,如图1所示.图1中,Pi为质点,质点Pi和Pj间的联接为弹簧.在曲面展开成平面的过程中,如果平面上Pi和Pj的间距大于对应的原始曲面上此两点的间距,则对Pi和Pj施以拉力(图1中P0和P1点);反之,则施以推力(图1中P0和P6点).
弹性变形能E和弹性力f的计算式为
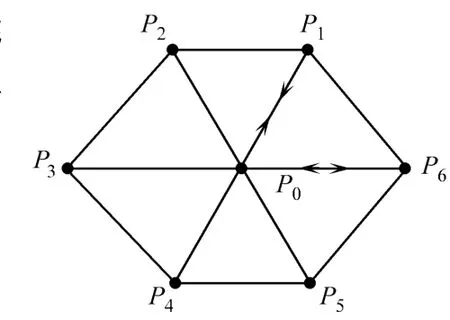
图1 弹簧质点系统Fig.1 Sp ring-mass system
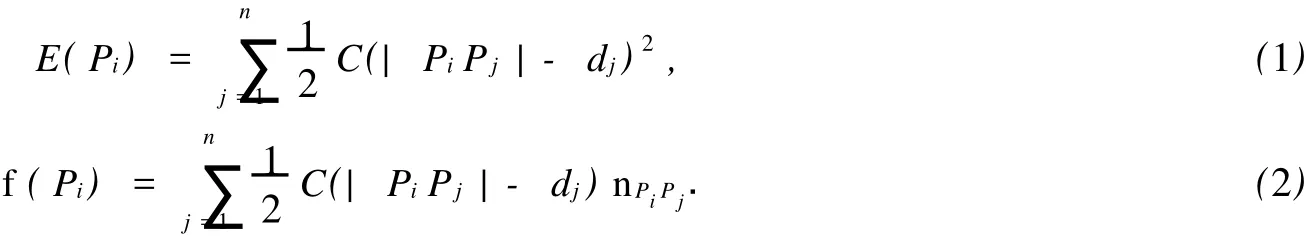
上式中:C为弹簧弹性变形系数;|Pi Pj|是曲面展开后的平面上Pi到Pj的距离;dj为空间曲面上的Pi到Pj的距离;是从Pi指向Pj的单位矢量,n为质点Pi相邻的质点数.
在曲面展开过程中,质点的运动可以用拉格朗日方程来描述,即

式(3)中:M,D和K分别为系统的质量矩阵、阻尼矩阵和刚度矩阵;gq为局部自由度与全局自由度之差引起的系统内力,fq为系统外力.
在弹簧系统中,gq和fq为零,而阻尼矩阵D可以忽略,所以拉格朗日方程可简化为

当考虑质点运动中的时间间隔Δt很小时,质点Pi的加速度可被认为是常量,则整个系统中的各个质点处于平衡.利用欧拉法可以求解式(4)的拉格朗日方程,即式(4)可变换为

式(5)中:mi是节点Pi的质量;ζ是曲面的面密度;fi(t)是作用在节点Pi上的弹性力;Ak是包含节点Pi的所有三角形中第k个三角形的面积;¨q(t)是节点Pi的加速度;˙q(t)是节点Pi的速度;qi(t)是节点Pi在时间t的位置.
1.2 算法的改进
为了得到精确的展开平面,需要进行能量算法的多次迭代.从式(5)的第3个式子可以看出,前一时刻的速度对后一时刻的速度是有很大影响的.当迭代次数较多时(一般复杂曲面要进行很多次的迭代),惯性作用会产生累积效应,导致的后果是在当前时刻得到的质点速度非常大.即使后一时刻加速度与前一时刻速度是反向的,质点的运动也不能立即反向,而是会继续向原来方向运动.这样就会导致越来越偏离平衡位置,网格边长的变形程度越来越厉害,最终的结果是在曲面展开中产生较大的振荡.曲面越复杂,这种副作用就越明显,以致得不到符合需要的展开平面.
为了避免这种不利的副作用,采取忽略初速度的方法,对式(5)中的第3,4式进行调整,即

采取忽略初速度的初衷是为了避免发散现象.若优化的时间Δt过小,曲面展平的优化速度太慢,迭代次数过多,展开时间过长,所得到的优化效果不明显;若优化的时间Δt过大,展平过程中会引起迭代振荡,得不到所需的展开平面.所以,如何取优化时间Δt是算法的关键.
适当地选取优化时间,可避免初始时间步长取值不合适而浪费大量的计算时间或迭代发散的情况.Δt是随着迭代次数的增多而不断减小,其计算式为

式(8)中:t0是初始优化时间;dt为迭代过程中每次优化时间的变化量;N为算法的当前迭代次数;M为Δt变化一次所需的迭代次数.
在算法迭代的初期,为达到优化的高效率目的,适当选取较大的t0值(这里取t0为0.5~0.6).随着迭代次数的增加,质点离平衡点越来越近,此时,Δt应当取较小值,以防止振荡现象的产生.在算法中,为了防止Δt过小,甚至为负值的情况发生,就必须合理地选取dt,N和M.实验结果表明,若参数dt,N和M选取不当,使Δt变化缓慢,则容易发生展开震荡;或使Δt变化过快,导致展开精度不佳.
1.3 评判准则
不可展曲面的展开不可避免地会发生变形.角度误差、面积误差和边长误差都可以作为衡量展开精度的衡量标准.在这里,主要考虑面积误差和边长误差.在曲面展开过程中,原始曲面和展开平面的面积会有所不同,而三角形网格上的边长也会发生变化,其相对面积误差(eS)和相对形变误差(eL)[8-9]为

式(9)中:S是曲面片展开前的实际面积;S′是曲面展开后所对应的的面积;L为曲线段在展开前的实际长度;L′是展开后曲线段所对应的长度.
2 曲面展开
2.1 初始曲面的展开
2.1.1 不含能量释放的展开 无约束和有约束的三角片的展开,如图2,3所示.
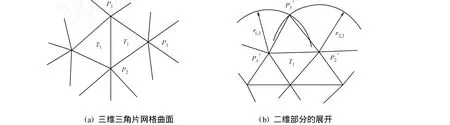
图2 无约束的三角面片展开Fig.2 Unconstrained triangle flattening
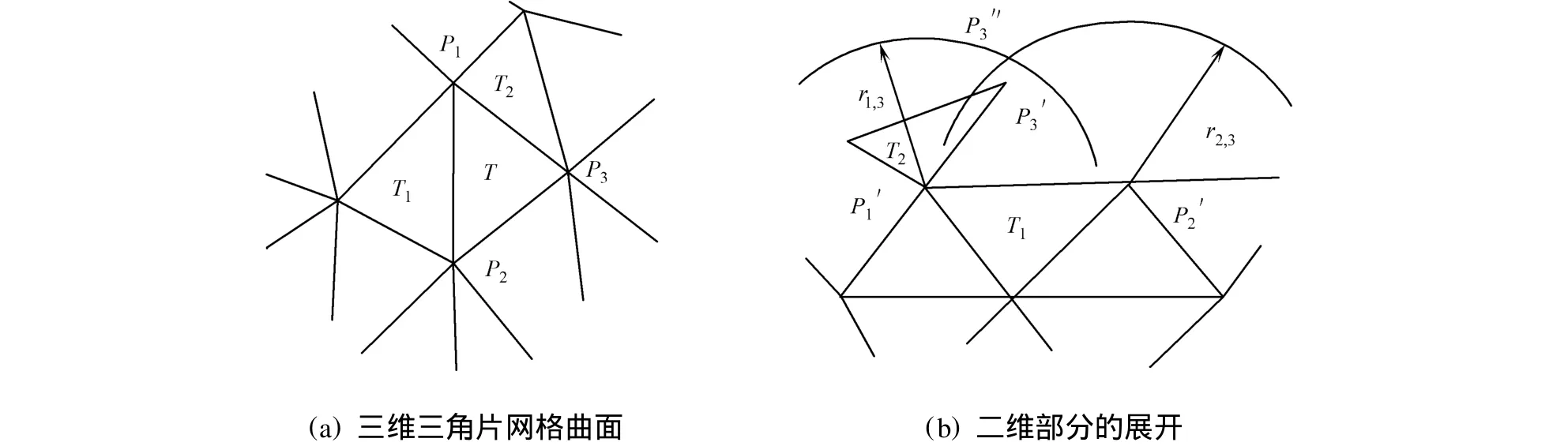
图3 有约束的三角面片展开Fig.3 Constrained triangle flattening
由图2可知,P1P2是三角面片T1和T的共边.当三角面片T1已经展开,而三角面片T未展开.即T的两个点P1和P2的位置已经在二维平面确定(即P′1和P′2),而点P3在二维平面的位置尚未确定时,以P′1和P′2为圆心的两个圆的交点来确定(圆的半径分别为r1,3和r2,3)点P′3的位置,r1,3和r2,3的长度即为它们在空间网格上的长度,所有点的第1次展开都是以无约束方法得到的.
包含点P3的三角面片有多个,由这些三角形面片展开的P3的点位置也有多个.当曲面是可展曲面时,所求的这些点位置是一致的.当曲面是不可展曲面时,这些点位置有可能不一致.此时,会有层叠和裂缝的现象产生,影响曲面展开的精度,甚至曲面展开的获得.一般所展开的曲面大部分是不可展曲面,所以必须考虑带约束的三角片展开.
由图3可知,假设包含P3点的三角片T2已展开,这时P3在由已展开T2所决定的二维平面中的位置为P′3.若不采取有约束的展开方法,当继续展开T时,由T展开时所决定的P3的位置为P″3.很明显,这两点的位置并不一致.为了使P3在二维平面具有唯一性,可以取两点的平均位置作为P3在二维平面的对应点来初步解决这个问题.
但是,此方法肯定有相当大的误差,将会产生弹性能量,导致层叠或裂缝现象的发生,必须采取适当的方法来尽可能地减少这个误差.对此,可以采取能量释放方法来初步减少误差.
2.1.2 含能量释放的方法 在对三角片进行有约束的展开时,为了使展开点具有唯一性,可采取平衡位置的方法.这样所造成的后果是原始曲面的曲线长度与其展开后的长度存在很大的误差,使得面积误差和形状误差很大,不利于曲面的精确展开.通过释放在位置平均处理过程中产生的弹性能量,可以解决这个问题.
曲面上所有网格化三角形根据上述无约束展开或约束展开方法展开为平面三角形后,得到曲面的初始展开平面网格;然后,用式(5)计算三角网格上的每个点的能量,通过释放能量来改善展开的平面.如果整张展开网格曲面有m个离散点,则所有离散点的展开变形能为

展开变形能的大小反映曲面整体展开变形程度.为了减小展开的变形,需要能最大程度地减小变形能,释放变形能.
2.2 能量展开算法
能量展开算法主要有如下7个步骤.
(1)建立3个集合V,A和F.V为包含所有尚未展开的曲面三角形的集合;A为有序活动集合,即从集合V中挑选出来的三角形集合,这些三角形是与已展开三角形共边而将要被展开的三角形;F为所有已展开到二维平面的三角形集合.对这3个集合进行初始化,把所有要展开的空间三角形添加到集合V中,置集合A和F为空.
(2)从V集中选择展开基本三角形T0.一般在曲面的对称中心或曲率较大的部位选择该三角面片,然后将其无约束展开在平面上任意位置,并将该基本三角形从V中删除,直接加入到F中.
(3)在V集中寻找与基本三角形T0共边的所有三角形{Ti}.将这些三角形加入到A集中,并从V中减去.
(4)判断A集是否为空.如果A集不为空,则从A集中取出下一个三角形Ti,并按步骤(5)或步骤(6)的方法展开;如果A集为空,则判断V集是否为空;如果V集为空,则转到步骤(7)执行;否则,转到步骤(3)执行.
(5)如果三角形的第3点还没有展开(其余两点已在展开集F的某个三角形中),此时采用三角形无约束展开,并将三角形Ti加入到展开集F中;然后,从A中减去Ti,转到步骤(4).
(6)如果三角形Ti的第3点在前面的三角形展开中已经展开,并形成平面三角形,则用三角形约束展开方法进行展开.处理后,将三角形Ti加入到展开集F中,从A中减去,然后转到步骤(4).
(7)分别计算面积误差eS和形变误差eL,以及所有离散点的展开变形能E(φ′),判断其值是否是在阀值内.若误差都小于阀值,则说明已得到优化的曲面展开;若误差大于阀值,则回到步骤(3)重新进行能量释放,直到超过迭代次数N为止.
3 应用实例
算法已通过VC 6.0编程在微机上实现,图4是用能量模型所作的曲面展开示例.该曲面有189个顶点,306个三角形.
当时间初始步长dt=0.6时,如果在迭代中不采取改变时间步长的方法,很容易出现发散;而采取改进算法后,面积误差为1.455%,形变误差为0.988%,基本符合精度要求.
当时间初始步长dt=0.3时,如果在迭代中不采取改变时间步长的话,虽然不会出现发散的情况,但其面积误差为4.668%,形变误差为2.456%,展开质量不是很好.
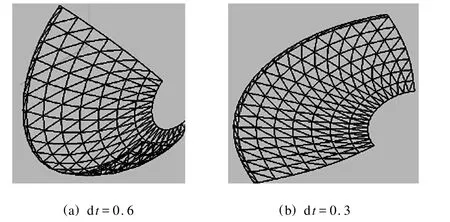
图4 曲面展开实例Fig.4 Example of surface flattening
4 结束语
运用能量模型的展开算法,可以很好地解决一般的曲面展开问题,而且计算量较小,不需要解大规模线性方程组.绝大部分的曲面可以三角网格化,所以能量模型算法具有很强的通用性.在实验结果中发现,时间步长、弹性系数和面密度都直接影响到曲面展开的质量.改进算法主要研究时间步长对算法的影响,而下一阶段的目标是考虑以上3个参数的合理配取,以期达到更好的展开结果.
[1]席平.三维曲面的几何展开[J].计算机学报,1997,20(4):315-322.
[2]毛国栋,孙炳楠,徐浩祥.基于弹簧-质点系统的薄膜结构曲面展开算法[J].浙江大学学报:工学版,2005,39(8): 1238-1242.
[3]王弘,王昌凌.基于能量模型的曲面展开通用算法[J].计算机辅助设计与图形学学报,2001,13(6):556-560.
[4]梁伟文.基于弹性模型的三角网格曲面优化展开[J].塑性工程学报,2007,14(1):129-132.
[5]雷军鹏.一种基于能量法的自由曲面展开算法[J].机械设计与制造,2007(4):28-30.
[6]徐荣璋,刘晓毅,陈军.曲面展开方法的发展现状[J].模具技术,2002(5):15-18.
[7]杨继新,刘健,肖正扬.可展面在平面上的展开及其在工程上的应用[J].机械科学与技术,2001,20(5):201-202.
[8]SH IMADA T,TADA Y.Development of curved surface using finite element method[M].New York:Sp ringer-Verlag,1989:23-30.
[9]M ETAXASD N.Physics-based deformable models:Applications to computer vision,graphics,and medical imaging[M].Boston:Kluwer Academic Publishers,1997.
(责任编辑:陈志贤英文审校:郑亚青)
An Improved Algorithm for Surface Flattening Based on Energy Model
YAN Guo-biao,L IU Bin
(College of Mechanical Engineering and Automation,Huaqiao University,Quanzhou 362021,China)
In allusion to occurring problems of existing algorithm s,an imp roved algorithm of surface flattening based on energy-model is presented.The imp roved algorithm is mainly to adjust time-step to avoid divergent phenomenon in the course of flattening,at the same time enhance the quality of the flattened surface,and better eliminate oscillating phenomena caused by too many iterative numbers.The results of case study have show n that the imp roved algorithm is effective, and can conform to the requirement of real-time and interactive design.
surface flattening;energy-model;time-step;triangular mesh
TP 391.7
A
1000-5013(2011)02-0135-05
2009-11-12
刘斌(1972-),男,副教授,主要从事聚合物材料模塑成型的研究.E-mail:mold_bin@hqu.edu.cn.
福建省科技计划重点项目(2009H0032);福建省自然科学基金资助项目(E0810040);国务院侨办科研基金资助项目(08QZR01)

