布拉德福定律在专利文献中应用的可行性研究

吕义超 刘红光 王 君

(江苏大学科技信息研究所 镇江 212013)

·情报分析·

布拉德福定律在专利文献中应用的可行性研究

吕义超 刘红光 王 君

(江苏大学科技信息研究所 镇江 212013)

基于专利文献与期刊文献的相似性，以“混合动力汽车”专利文献为例，分别运用布拉德福定律区域法、图形法和计算法对其进行分析，通过考察其结果的统一性和一致性，来研究布拉德福定律在专利文献中应用的可行性，并对其在应用中遇到的相关问题进行讨论。

布拉德福定律 专利 混合动力汽车

1 引言

为了探明文献的分布规律，英国著名文献学家S·C·布拉德福于1934年首先提出了布拉德福定律，它定量地揭示了科学论文在期刊中的集中与离散分布规律，其文字表述为：如果将科技期刊按其刊载某专业论文的数量以递减顺序排列，则可分出一个核心区和相继的几个区域，每区刊载的论文量相等，此时核心期刊和相继区域期刊数量成1∶a∶a2……的关系[1]。

布拉德福定律问世以来，引起了图情界的广泛关注，经过维克利、莱姆库勒、布鲁克斯和埃格等人的发展，不仅在理论上得到了极大的完善，而且在应用研究上也取得了一些成果。目前应用范围主要包括：①确定核心期刊；②确定某学科的核心出版社；③确定核心作者和高被引作者；④确定图书馆的核心读者；⑤图书馆馆藏建设；⑥检索工具完整性的测定；⑦对网页、网站的集中分散程度进行计量分析研究[2-5]。国外有学者根据布氏定律，按照科技发展程度以及科技依赖性将国家分为核心区、中间区和外围区，以此来进行国际科技发展指标的分析[6]。另外，也有文献认为可以将布拉德福定律应用于专利分析过程中[7]，但是否可以将其应用于专利文献中，在国内外已公开文献中相关实例验证还比较少见。

2 布拉德福定律在专利文献中应用的可行性分析

专利文献是各国专利局及国际性专利组织在审批专利过程中产生的官方文件及其出版物的总称[8]。这些文献是世界上最大的公开技术信息源之一，它包含了世界上90%～95%的技术信息。通过研究，我们发现专利文献有着和期刊文献相类似的性质。例如：某个技术领域可类比某个学科或专业，某个专利权人(IPC号或发明人，下同)可类比某种期刊，专利权人申请的一件专利可类比期刊上所刊载的一篇论文，而某技术领域的专利在各个专利权人中的分布，与某学科的论文在各种期刊上的分布呈现着相似的集中与离散分布趋势。基于此，我们假设，主要用于研究期刊文献分布规律的布拉德福定律，可推广应用于专利文献，以IPC分类号为例，则可以用文字表述为：如果将IPC分类号所包含的某技术领域专利数量的多寡，以递减顺序排列，则可分出一个核心区和相继几个区域，每区包含的专利量相等，此时，核心区IPC号数量和相继区域IPC号数量成1∶a∶a2……的关系。

本文拟以“混合动力汽车”相关专利文献为例，通过运用布拉德福定律区域分析法、图形法和计算法分别对其进行实证分析，来考察布拉德福定律在专利文献中应用的可行性。

2.1 数据准备

布拉德福定律的应用具有一定的限制性条件[2]，对于专利文献而言，这种限制性条件可以表述为：首先，所应用的技术领域应当清楚划定；其次，对所分析技术领域内专利数据的统计应当是充分的；第三，被分析专利的期限应当清楚划定。为了满足以上条件，本文采用以下数据采集的方法：以中国国家知识产权局公开的专利作为数据源，运用关键词和IPC分类号相结合的方法，在题名和摘要中将关键词(混合动力 OR双动力 OR多动力 OR 复合动力 OR 混合驱动 OR 复合驱动)与(汽车 OR 客车 OR 公交车 OR 轿车 OR 电动车 OR 乘用车)相结合，同时在IPC中检索(B60 OR F01 OR F02 OR H01 OR H02)，并剔除B62，检索公开日在2000年至2009年的混合动力汽车专利，截止2010年3月31日，共检索得到1 510件专利，经过数据清洗，最终得到有效数据1 354项，即为本文所要分析的对象。

2.2 “主分类号——专利数量”模式分析

将布拉德福定律应用于“主分类号——专利数量”模式的分析中，可以根据专利数量确定该技术领域内的核心专利分类号，进而确定核心技术领域。统计检索得到的1 354项有效数据，共涉及342个主分类号，然后计算出每个主分类号所标识的专利数量，根据“等级排序”的思想，将其所标识的专利数量按递减顺序排列，得到“主分类号——专利数量”模式的等级排序表(表1)。

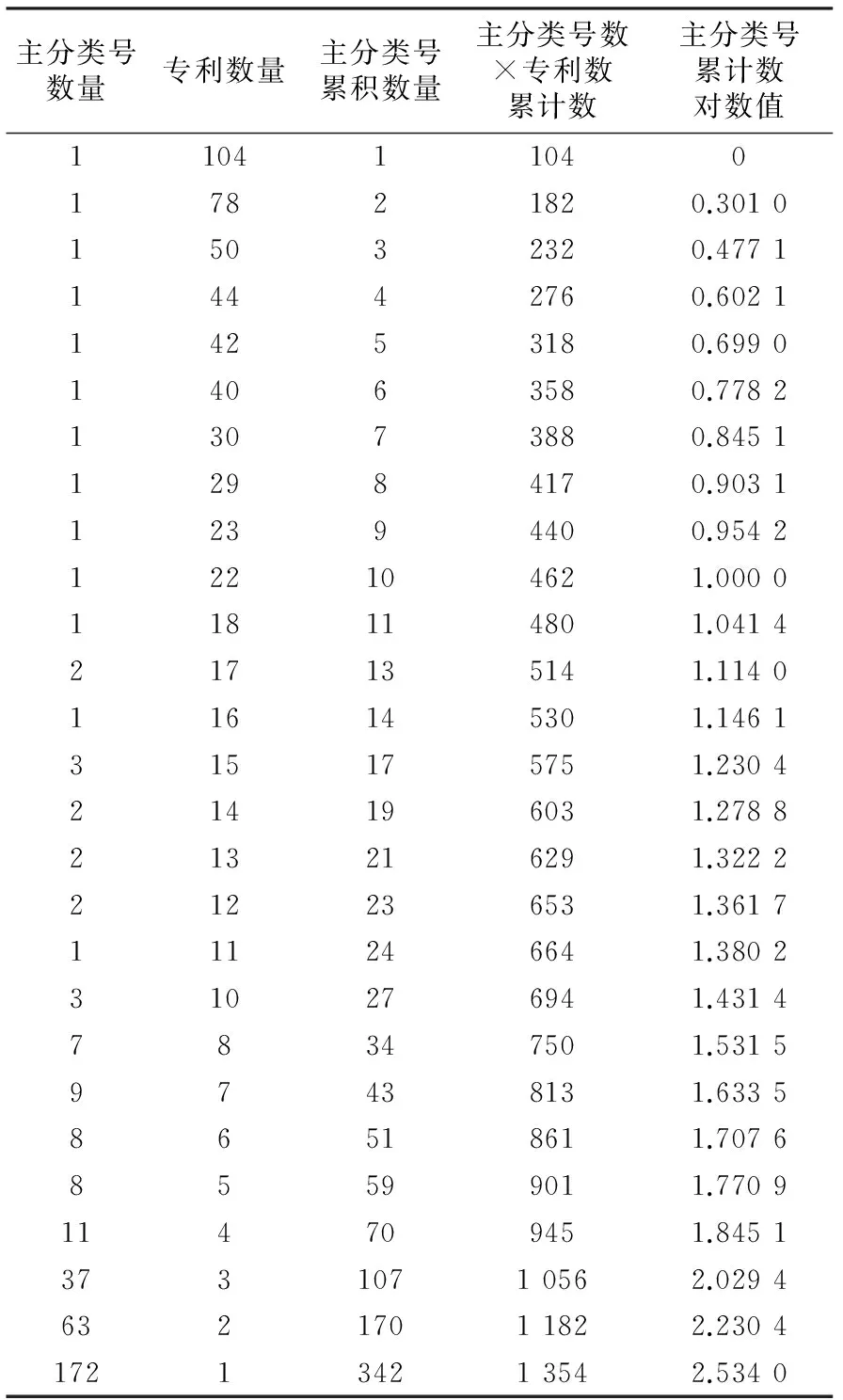
表1 我国混合动力汽车专利文献统计数据(1)

2.2.1 区域法 首先，按照布拉德福定律区域法的思想，将所有专利按照主分类号分为3个区，使每个区的专利数量大致相等，得到表2。从表2中可以看出，当每区专利数量大致相等时，相应的主分类号累计数量大致呈等比关系，其布拉德福系数为5.56和5.66，平均值为5.61。

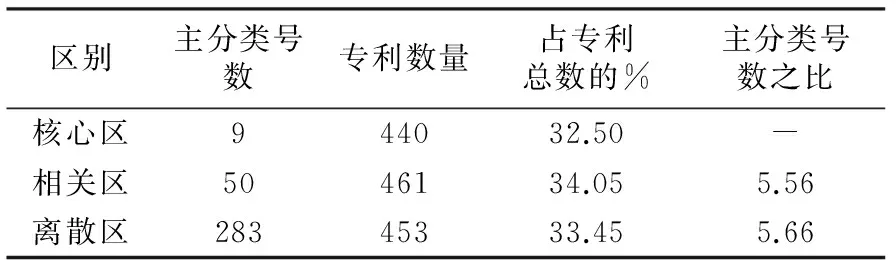
表2 布拉德福定律分布表(n=3区)

采用同样的方法，再将所有专利依次分为4区、5区、6区和7区，同样使每区的专利数量大致相等，统计每区主分类号的累计数量，并由此计算相应的布拉德福系数、平均值及其标准差(用来衡量布拉德福系数的离散程度)。

当n=4区时，各区主分类号累计数量分别为：5、19、68、249；布拉德福系数为：3.80、4.37、2.83，平均值为3.67，标准差为0.78；

当n=5区时，各区主分类号累计数量分别为：4、11、28、64、235；布拉德福系数为：2.75、2.55、2.29、3.67，平均值为2.82，标准差为0.60；

当n=6区时，各区主分类号累计数量分别为：3、7、14、35、111、172；布拉德福系数为：2.33、2、2.5、3.17、1.55，平均值为2.31，标准差为0.60；

当n=7区时，各区主分类号累计数量分别为：2、5、10、17、36、100、172；布拉德福系数为：2.5、2、1.7、2.12、2.78、1.72，平均值为2.14，标准差为0.43。

从上述对混合动力汽车领域专利文献进行的区域法描述，可以看出：当将专利文献分为不同区数时，其各区主分类号累计数量大致都呈现等比趋势，具有布拉德福分布的特点。

2.2.2 图形法 根据表1的数据，以主分类号累计数量的对数lg (n)为横坐标，以相应的专利文献累积数R (n)为纵坐标进行图象描述，制得图1所示的一条曲线。图中该曲线可以分为两段：曲线AC和直线CB，两线的转折处为C点(曲线与其切线的交点)，其中AC一段曲线对应于核心区，而直线BC则对应于核心区以后的相继各区，基本符合布拉德福分散定律的图形表示，而C点的横坐标对应点为n=10，这一结果与区域法的结果基本一致。

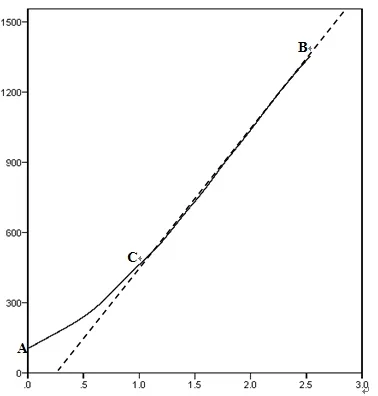
图1 我国混合动力汽车专利文献分布曲线

2.2.3 计算法 布拉德福定律问世以后，引起了许多情报学者的兴趣，他们对该定律在各种专业文献中的具体运用进行了广泛的研究。如比利时的埃格博士曾于1986年提出了一个布拉德福离散系数计算法，其公式是[9]：

m=(eE·Y)1/n(1)

1990年埃格又提出一个核心区数量计算法，其公式是：

P=2ln(eE·Y) (2)

在公式(1)和公式(2)中：

m为布拉德福离散系数；

n为分区数目；

Y为标注专利文献最多的主分类号所标注的专利数量；

P为核心区数量；

E为欧拉系数，E=0.5772。

现将有关数据代入公式(1)和公式(2)中，其计算结果如下：

当n=3时，

m=(2.7180.5772×104)1/3=5.7003≈5.70

当n=4时，

m=(2.7180.5772×104)1/4=3.6891≈3.69

当n=5时，

m=(2.7180.5772×104)1/5=2.8414≈2.84

当n=6时，

m=(2.7180.5772×104)1/6=2.3876≈2.39

当n=7时，

m= (2.7180.5772×104)1/7=2.1084≈2.11

P=2ln(2.7180.5772×104)=10.4431≈10

可以看出，由上式算出的布拉德福离散系数和核心区数量近似值与区域法及图像法的结果基本一致，或相差不大。这说明将我国混合动力汽车领域的专利数量按主分类号进行排列，符合布拉德福分布规律。

3结论与讨论

综合考虑布拉德福定律的区域法、图形法和计算法的结果，得出我国混合动力汽车技术领域所使用的核心区主分类号有10个，分别是：B60W20/00、B60K6/02、B60W10/06、B60K6/04、B60K6/20、B60K6/00、B60L11/18、B60K6/48、B60L11/00、B60K6/12，其对应的具体技术领域可以通过IPC分类法查得。

为了更充分验证布拉德福定律在专利文献中应用的可行性，本文还采用同样的方法将布拉德福定律在“专利权人——专利数量”模式中的应用情况做了分析。统计检索得到的1 354项有效数据，共涉及358个第一专利权人(以下简称专利权人)，然后计算出每个专利权人申请的专利数量，根据“等级排序”的思想，将各个专利权人申请的专利数量按递减顺序排列，得到“专利权人——专利数量”模式的等级排序表(表3)。从分析和对比结果来看，除了核心区专利权人数量的一致性不太理想外(主要原因是由于混合动力汽车的研发还处于产业发展的初期，所以出现了“寡头垄断”现象，即一个或很少的几个专利权人的专利申请数量远远高于其他专利权人)，其他数据基本令人满意，基本符合布拉德福定律分布的特点。

表3 我国混合动力汽车专利文献统计数据(2)

由于专利文献的特点，某一特定技术领域难以准确划定，所以此技术领域专利数量的完整性就会受到影响，而这些都是应用布拉德福定律的重要限制条件，因此，在将布拉德福定律应用到专利文献时，如何准确划定专利技术领域和确保专利文献的完整性是必须认真考虑的。

经过上文的初步分析，我们认为将布拉德福定律应用到专利文献中是基本可行的，但这个结果还需要更多资料的验证。另外，布拉德福定律是否可以在“(第一)发明人——专利数量”模式中应用，是否可以将此定理应用于专利文献上的所有分类号、所有专利权人和所有发明人，或者其他领域等，还需要做更深入的研究。

[1] 周任材,林端宜. 布拉德福定律在中医药学外文核心期刊研究中的应用[J]. 情报探索,2008(1):18-19.

[2] 岳一凡,张锦顺. 布拉德福定律应用现状研究综述[J]. 学理论,2009(19):179-180.

[3] 邱均平. 文献信息离散分布规律——布拉德福定律[J]. 情报理论与实践,2000(4):315-320.

[4] 曹作华. 论帕累托原则与布拉德福定律对馆藏建设的综合效用[J].图书情报工作,2004,48(3):22-25,7.

[5] 欧阳显菊. 测定图书馆核心读者的统计分析方法[J]. 现代情报,2004(12):12-13.

[6] H.Eto,P.M.Candelaria. Applicability of the Bradford distribution to international science and technology indicators[J].Scientometrics,1987,11(1): 27-42.

[7] 方 曙,张 娴,肖国华. 专利情报分析方法及应用研究[J]. 图书情报知识,2007(4):64-69.

[8] 李建蓉.专利文献与信息[M].北京:知识产权出版社,2002:8.

[9] 赵玉珍. 运用布拉德福定律研究中国沙棘文献的核心期刊[J]. 情报科学,2000,18(5):462-464.

AStudyoftheFeasibilityoftheApplicationofBradford’sLawinPatentDocuments

Lv Yichao, Liu Hongguang, Wang Jun

Institute of Science and Technology Information, Jiangsu University, Zhenjiang 212013, China

Based on the similarity between patent documents and journal articles, this paper takes the patent documents of the hybrid electric vehicle as an example, and analyzes it with the regional law, the graphic method and the calculation method of Bradford’ s law. It then studies the feasibility of applying Bradford’ s law to patent documents by examining the uniformity and the consistency of the results. Finally, it discusses the problems in application of Bradford’ s law.

Bradford’ s law; patent; hybrid electric vehicle

G350

吕义超，男，1985年生，江苏大学科技信息研究所2008级情报学硕士研究生，发表论文3篇；刘红光，女，1956年生，副教授，硕士生导师，发表论文40余篇；王 君，女，1985年生，江苏大学科技信息研究所2008级情报学硕士研究生，发表论文3篇。