严格F－G广义凸函数

赵 宇，黄金莹，刘春妍

（佳木斯大学理学院，黑龙江 佳木斯 154007）

严格F－G广义凸函数

赵 宇，黄金莹，刘春妍

（佳木斯大学理学院，黑龙江 佳木斯 154007）

给出一类新的广义凸函数——严格F－G广义凸函数，并给出条件P1、P2及其性质，研究严格F－G广义凸函数的若干性质，给出严格F－G广义凸函数的两个充分条件，指出在一定条件下，满足中间点严格F－G广义凸性的F－G广义凸函数是严格F－G广义凸函数，满足中间点严格F－G广义凸性的半严格F－G广义凸函数是严格F－G广义凸函数．最后给出严格F－G广义凸函数在极小化问题中的一个实际应用．

严格F－G广义凸函数；F－G广义凸函数；条件P1；条件P2

凸性及广义凸性是不等式研究的主要内容，同时也在最优化理论方面起着重要作用．近20年间，在文献中出现了各种各样的广义凸函数，其中比较常见的推广方式是以讨论极值问题最优性条件为目的通过将凸性条件弱化来构造的广义凸函数．1981年，Hanson［1］和Craven［2］提出了不变凸、拟不变凸和伪不变凸函数等概念，并利用其条件建立了分式规划对偶理论．1985年，Jeyakumar［3］提出预不变凸函数的概念，1991年，Pini［4］定义了更广义的预不变拟凸函数．值得一提的是，1995年S．R．Mohan与S．K．Neogy［5］提出了条件C，条件C所蕴含的等式关系搭建了不变凸函数类之间的关系，推导出严格、半严格预不变（拟）凸函数的若干判别准则，极大促进了不变凸函数类的性质研究．近几年，国内的专家学者针对上述各类广义凸函数开展了特性研究，唐万梅等［6－7］研究了强预不变凸函数和强预拟不变凸函数的充要条件，刘彩平［8］研究了半严格不变凸函数，丰富了无限维空间中的广义凸理论，黄金莹等［9－10］对预不变凸函数的性质做了进一步研究，提出F－G广义凸函数概念．

由于它们在一定程度上又保留了凸函数的良好性质，所以各类广义凸函数之间必然有着类似的性质，在研究方法和技巧上就不可避免地出现了类比、雷同、重复的现象，且在处理具体问题时又受到具体形式的影响．该文建立严格F－G广义凸函数概念，开展一般性研究，将目前相关结果加以整合、梳理和推广．

1 严格F－G广义凸函数

定义1 称集合K⊂Rn是关于F的广义凸集，若存在向量值函F：K×K×［0，1］→Rn，使得∀λ∈［0，1］，∀x，y∈K，有F（x，y，λ）∈K．

将上述中K⊂Rn换成D⊂R，则会有：称集合D⊂R是关于G的广义凸集，若存在数量函数G：D×D×［0，1］→R，使得 ∀λ∈ ［0，1］，∀s，t∈D，有G（s，t，λ）∈D．

定义2 设K⊂Rn是关于F的广义凸集，D⊂R是关于G的广义凸集，称数量函数f：K→D在K上是F－G 广义凸函数，若 ∀λ∈ ［0，1］，∀x，y∈K，有f［F（x，y，λ）］≤G［f（x），f（y），λ］．

定义3 设K⊂Rn是关于F的广义凸集，D⊂R是关于G的广义凸集，称数量函数f：K→D在K上是严格F－G 广义凸函数，若 ∀λ∈ （0，1），∀x，y∈K，且x≠y，有f［F（x，y，λ）］＜G［f（x），f（y），λ］．

特别地，在上述定义中，当特取D⊂R为凸集，并且G（s，t，λ）＝λs＋（1－λ）t，∀s，t∈D，则称数量函数f：K →D 在K 上是严格F 凸函数．当特取G（s，t，λ）＝max｛s，t｝，∀s，t∈D，则称数量函数f：K →D在K上是严格F拟凸函数．

注1［1］取K⊂Rn为关于向量函数η：Rn×Rn→Rn的不变凸集，D⊂R为凸集．

令F（x，y，λ）＝y＋λη（x，y），∀x，y∈K，λ∈ ［0，1］，G（s，t，λ）＝λs＋（1－λ）t，∀s，t∈D，则当数量函数f：K→D为K 上关于η的严格预不变凸函数时，f在K上是严格F凸函数．

注2［2］取K⊂Rn为关于向量函数η：Rn×Rn→Rn的不变凸集，D⊂R．

令F（x，y，λ）＝y＋λη（x，y），∀x，y∈K，λ∈ ［0，1］，G（s，t，λ）＝ max｛s，t｝，∀s，t∈D，则当数量函数f：K→D为K上关于η的严格预不变拟凸函数时，f在K上是严格F拟凸函数．

定义4 设K⊂Rn是关于F的广义凸集，D⊂R是关于G的广义凸集，称数量函数f：K→D在K上是半严格F－G 广义凸函数，若 ∀λ∈ （0，1），∀x，y∈K，且f（x）≠f（y），有

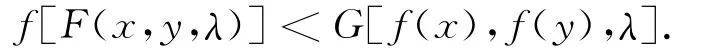
2 条件P1、P2

定义5 设K⊂Rn是关于F的广义凸集，称F在K 上满足条件P1、P2，若∀α，β∈［0，1］，且α＜β，∀x，y∈K，有

设D⊂R是关于G的广义凸集，称G在D上满足条件P1、P2，若 ∀α，β∈ ［0，1］，且α＜β，∀s，t∈D，有

对于条件P1、P2，有如下几个性质：

定理1 若F在K 上满足条件P1、P2，则 ∀λ∈ （0，1），∀u1，u2∈ ［0，1］，u1≠u2，∀x，y∈K，有

证明 ∀λ∈ （0，1），∀u1，u2∈ ［0，1］，u1≠u2，∀x，y∈K，

i）当u1＜u2时，由条件P1、P2得

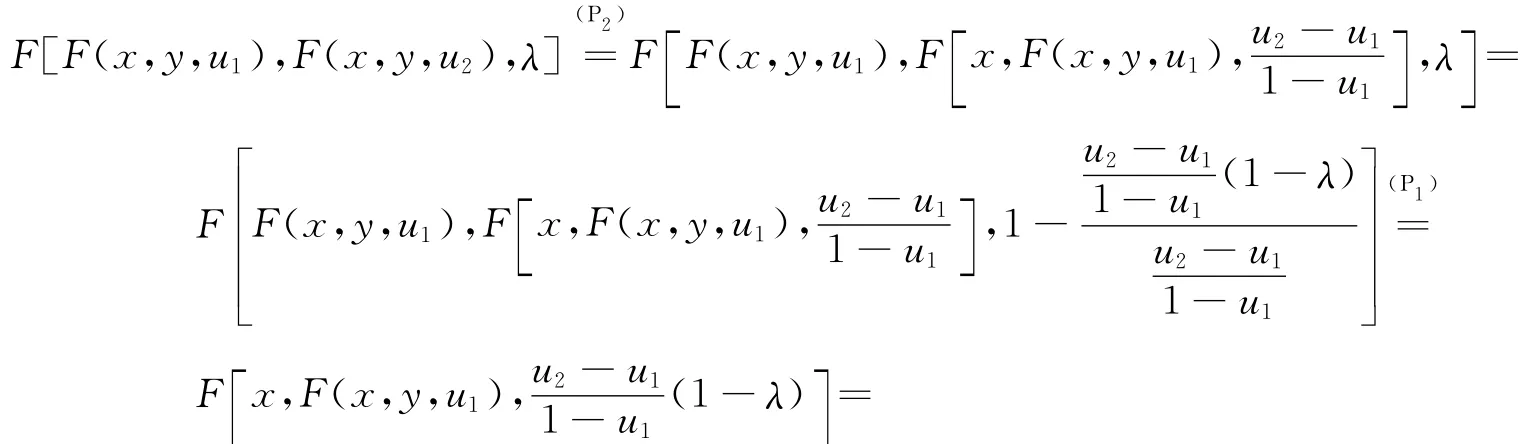
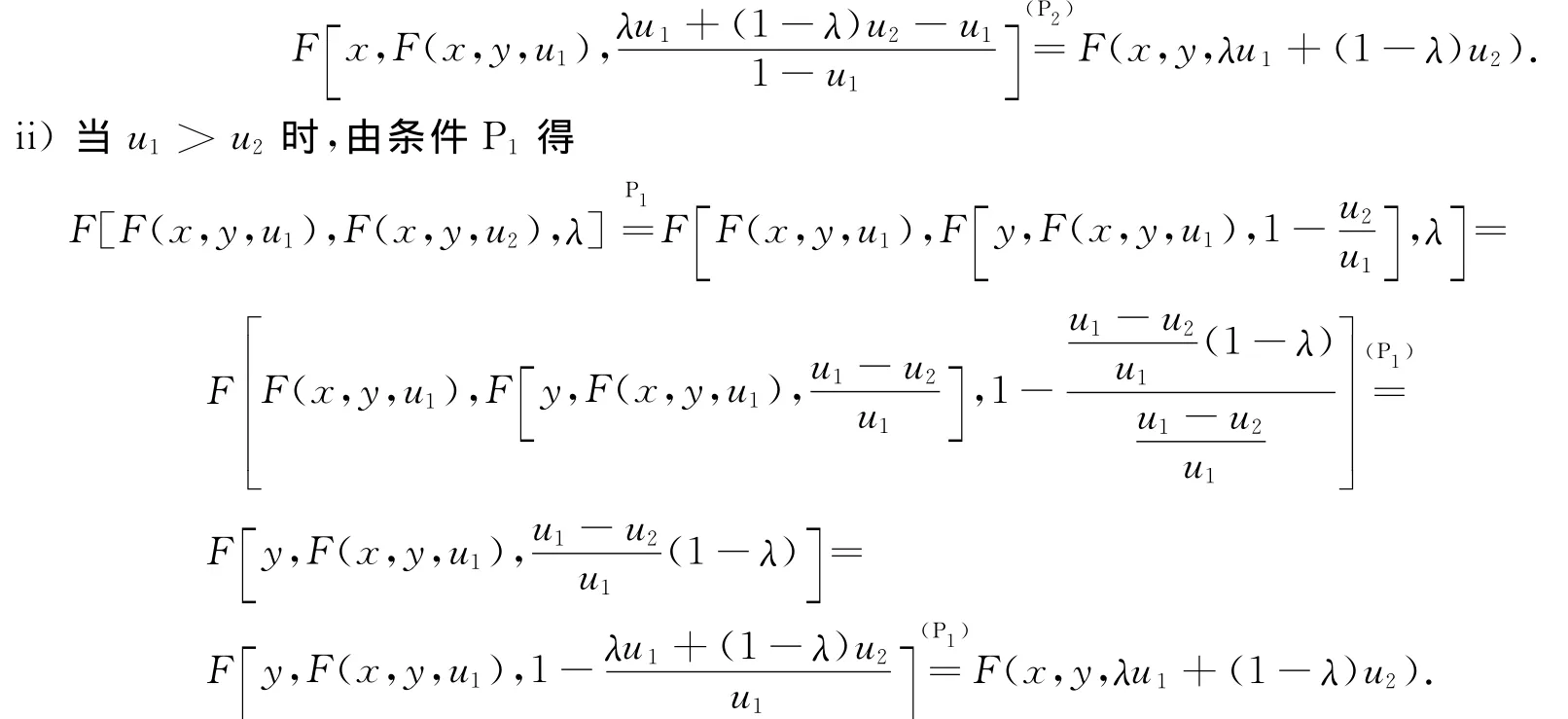
定理2 若K ⊂Rn是关于F 的广义凸集，且 ∀λ∈ ［0，1］，∀x，y∈K，有f［F（x，y，λ）］＝f［F（y，x，1－λ）］，则条件P1等价于条件P2．

故条件P2蕴含条件P1．

故条件P1蕴含条件P2．

定理3 若向量函数η：Rn×Rn→Rn在K 上满足条件C，则F（x，y，λ）＝y＋λη（x，y）在K上满足条件P1、P2．

证明 因η在K 上满足条件C，即 ∀λ∈ ［0，1］，∀x，y∈K，有

故F在K 上满足条件P1、P2．

3 严格F－G广义凸函数的性质

定理4 设f：K →D是严格F－G 广义凸函数．若 ∀λ∈ ［0，1］，∀s，t∈D，∀α＞0，有αs，αt∈D，且

推论1 设函数f：K→D是严格F凸函数，F满足条件P1、P2，∀λ∈（0，1），∀x，y∈K，且x≠y，有F（x，y，λ）≠y，则 ∀x，y∈K，且x≠y，Φ（α）＝f［F（x，y，α）］是［0，1］上的严格凸函数．

推论2 设函数f：K→D是严格F拟凸函数，F满足条件P1、P2，∀λ∈（0，1），∀x，y∈K，且x≠y，有F（x，y，λ）≠y，则 ∀x，y∈K，且x≠y，Φ（α）＝f［F（x，y，α）］是［0，1］上的严格拟凸函数．

下面给出严格F－G广义凸函数的2个充分条件．

定理9 设K⊂Rn是关于F的广义凸集，D⊂R是关于G的广义凸集，且有如下条件：

i）F、G在K 上满足条件条件P1、P2；

ii）∀λ∈ （0，1），G（s，t，λ）关于t在D 上严格增加；

iii）函数f：K→D在K 上是F－G广义凸函数，且满足∃α∈ （0，1），∀x，y∈ K，且x≠y，有f［F（x，y，α）］＜G［f（x），f（y），α］，则函数f在K上是严格F－G广义凸函数．

证明 令w ＝F（x，y，α），由条件iii）知，∀x，y∈K，x≠y，有

于是，对 ∀λ∈ （0，1），

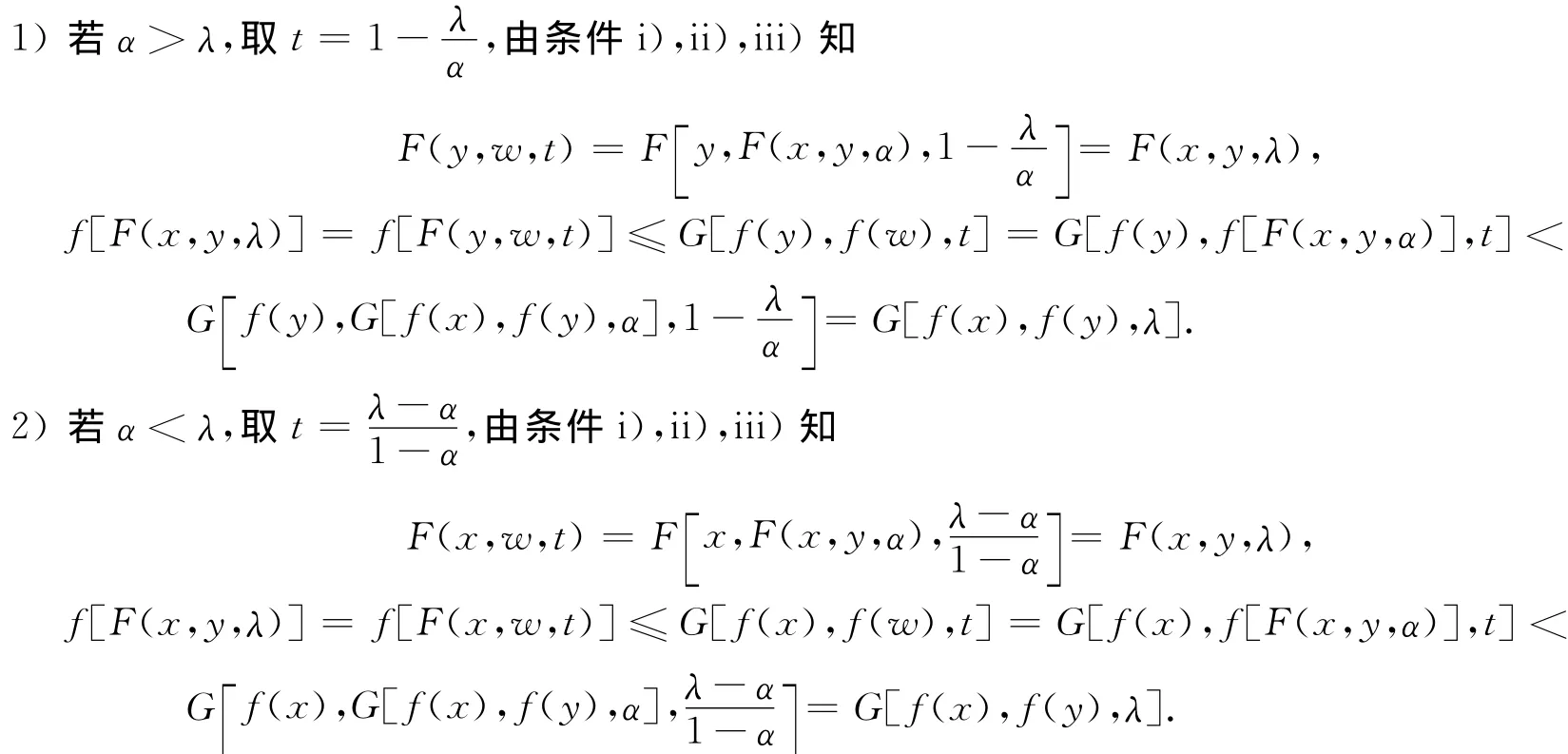
综上，函数f在K上是严格F－G广义凸函数．

定理10 设K⊂Rn是关于F的广义凸集，D⊂R是关于G的广义凸集，且有如下条件：

i）F、G在K 上满足条件条件P1、P2；

ii）G（s，t，λ）关于s，t在D 上非减，且对 ∀λ∈ （0，1），∀s，t∈D，有 min｛s，t｝≤G（s，t，λ）≤ max｛s，t｝；

iii）函数f：K→D在K 上是半严格F－G广义凸函数，且满足

∃α∈ （0，1），∀x，y∈ K，且x≠y，有f［F（x，y，α）］＜G［f（x），f（y），α］，

则函数f在K上是严格F－G广义凸函数．

证明 因为函数f：K→D在K上是半严格F－G广义凸函数，所以只须证明下式成立：

对 ∀λ∈ （0，1），f（x）＝f（y）且x ≠y，有f［F（x，y，λ）］＜G［f（x），f（y），λ］．

因为对 ∀λ∈ （0，1），∀s，t∈ D，有 min｛s，t｝≤G（s，t，λ）≤ max｛s，t｝，所以当f（x）＝f（y）时，G［f（x），f（y），λ］＝f（x）＝f（y）．

令w ＝F（x，y，α），由条件iii）知，∀x，y∈K，x≠y，f（x）＝f（y），有f（w）＝f［F（x，y，α）］＜G［f（x），f（y），α］＝f（x）＝f（y），于是，对 ∀λ∈ （0，1），

接下来作几个推论，将现有文献相关结论作为其特例．

推论3 设集合K是关于η的不变凸集，η满足条件C，如果f：K→R是预不变凸函数，且∃α∈（0，1），∀x，y∈K，x≠y，有f（y＋αη（x，y））＜αf（x）＋（1－α）f（y），则f是严格预不变凸函数．

根据定理3及定理9可以证明．

推论4 设集合K是关于η的不变凸集，η满足条件C，如果f：K→R是半严格预不变凸函数，且∃α∈ （0，1），∀x，y∈K，x≠y，有f（y＋αη（x，y））＜αf（x）＋（1－α）f（y），则f是严格预不变凸函数．

根据定理3及定理10可以证明．

推论5 设集合K是关于η的不变凸集，η满足条件C，如果f：K→R是预不变拟凸函数，且∃α∈（0，1），∀x，y∈K，x≠y，有f（y＋αη（x，y））＜ max｛f（x），f（y）｝，则f是严格预不变拟凸函数．

根据定理3及定理9可以证明．

推论6 设集合K是关于η的不变凸集，η满足条件C，如果f：K→R是半严格预不变拟凸函数，且∃α∈ （0，1），∀x，y∈K，x≠y，有f（y＋αη（x，y））＜ max｛f（x），f（y）｝，则f是严格预不变拟凸函数．

根据定理3及定理10可以证明．

4 严格F－G广义凸函数在极小化问题中的应用

考虑极小化问题（P）

［1］Hanson M A．On sufficiency of the Kuhn－Tucker conditions［J］．J Math Anal Appl，1981，80（2）：544－550．

［2］Craven B D．Invex functions and constrained local minima［J］．Bulletin of the Australian Mathematical Society，1981，24：357－366．

［3］Jeyakuaar V．Strong and weak invexity in mathematical programming［J］．Methods Oper Res，1985，55：109－125．

［4］Pini R．Invexity and generalized convexity［J］．Optimization，1991，22：513－525．

［5］Mohan S R，Neogy S K．On invex sets and preinvex functions［J］．J Math Anal Appl，1995，189（3）：901－908．

［6］Tang Wanmei，Yang Xinmin．The sufficiency and necessity conditions of strongly preinvex functions［J］．OR Transactions，2006，10（3）：50－58．

［7］Tang Wanmei，Liu Qian，Yang Xinmin．The sufficiency and necessity conditions of strongly prequasi－invex functions［J］．OR Transactions，2007，11（3）：21－30．

［8］刘彩平．半严格不变凸函数［J］．运筹学学报，2007，11（4）：85－92．

［9］黄金莹，赵宇，宋丽艳．预不变凸函数的若干性质［J］．哈尔滨师范大学学报：自然科学版，2009，25（3）：36－39．

［10］黄金莹，赵宇．关于半连续函数与凸函数的注记［J］．高等数学研究，2010，13（4）：91－93．

Abstract：This paper gives a new class of generalized convex functions－strictly F－Ggeneralized convex functions，and the conditions P1，P2as well as their properties．It studies on the properties of strictly F－Ggeneralized convex functions，gives two sufficient conditions of strictly F－Ggeneralized convex functions，and points out that under certain conditions，FGgeneralized convex functions which satisfies intermediate－point strictly F－Ggeneralized convexity is strictly F－Ggeneralized convex functions，and semi－strictly F－G generalized convex functions which satisfies intermediate－point strictly F－G generalized convexity is strictly F－Ggeneralized convex functions．And the paper provides a realistic application of strictly FGgeneralized convex functions in minimization problem．

Key words：strictly F－Ggeneralized convex functions；F－Ggeneralized convex functions；condition P1；condition P2

Strictly F－G Generalized Convex Functions

ZHAO Yu，HUANG Jin－ying，LIU Chun－yan
（College of Science，Jiamusi University，Jiamusi 154007，China）

O174．13 MSC2010：90C25；26B25

A

1674－232X（2011）01－0020－07

10．3969／j．issn．1674－232X．2011．01．005

2010－05－10

黑龙江省教育厅科学技术研究项目（11551499）．

赵 宇（1980—），女，黑龙江佳木斯人，讲师，硕士，主要从事凸分析与凸规划研究．E－mail：zhaoyu19800801＠sina．com