一类共振条件下三阶多点边值问题解的存在性

王 刚, 朱思念, 郑 婷

(中国矿业大学 理学院,江苏 徐州 221008)

有解 x(t)满足条件 (2)的充要条件是

事实上,若解 x(t)满足条件 (2),则从式 (5)有

根据条件 (C1),得到 Q1y=Q2y=0。另一方面,如果式 (6)成立,令

其中,a、b是任意常数,则易知 x(t)是方程 (5)且满足式 (2)的解,从而式 (4)成立。

一类共振条件下三阶多点边值问题解的存在性

王 刚, 朱思念, 郑 婷

(中国矿业大学 理学院,江苏 徐州 221008)

利用Mawhin的连续性定理及迭合度理论研究多点边值问题,讨论三阶非线性微分方程多点边值问题共振时解的存在性,获得解存在的充分条件,推广了现有的结果。

非线性微分方程;多点边值问题;迭合度

Abstract:This paper discusses the existence of solutions ofmulti-point boundary value problems for third-order nonlinear differetial equation at resonance by usingMawhin’s continuous theorem and coincidence degree theory and features the sufficient conditions for the boundary value problems,generalizing known results.

Key words:nonlinear differential equation;multi-point boundary value problem;coincidence degree

0 引 言

共振条件下边值问题因其在众多领域中的大量应用而受到了人们的广泛关注,取得了丰富的研究成果[1-9]。比如在工程学中,微分方程在共振条件下的边值问题常常被用来刻画梁在不同支撑条件下的静态形变。文献[1]讨论了几类二阶多点共振边值问题的可解性。多点边值问题是非局部边值问题的一种特殊情况,越来越多的人运用Mawhin连续性定理来研究多点边值问题,如文献 [2]研究的共振边值问题,其核是一维的。受此启发,笔者主要考虑非局部边值问题其中,f∈C[0,1]×R3是连续的,e(t)∈L1[0,1],0<ξ1<ξ2<… <ξm-2<1,0<η1<η2<… <ηm-2<1,αj∈R,βj≥0,在共振条件下解的存在性问题 (其核是二维的),通过应用迭合度基本知识及理论[9]建立该问题解的存在性的充分条件。

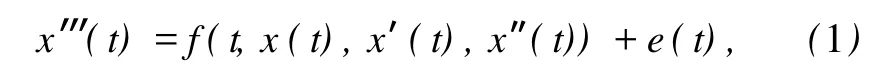
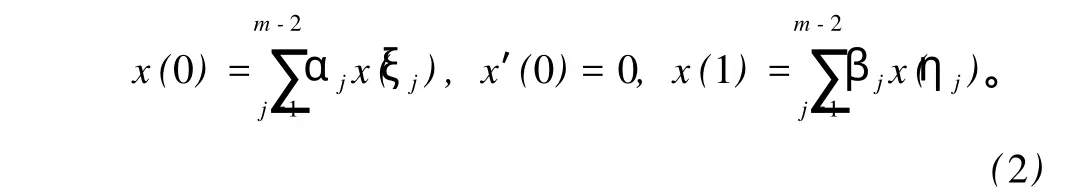
1 预备知识

定理 1[3](Mawhin连续性定理) 设Ω⊂Y是一个有界开集,L是一个指标为零的 Fredho lm算子,N是 L-紧的,如果下面条件成立:

2 主要结果

引理 1假设 (C1)、(C2)成立,则 L:domL⊂Y→Z是一个指标为零的 Fredho lm算子,投影算子Q:Z→Z可以被定义为

有解 x(t)满足条件 (2)的充要条件是

事实上,若解 x(t)满足条件 (2),则从式 (5)有

根据条件 (C1),得到 Q1y=Q2y=0。另一方面,如果式 (6)成立,令

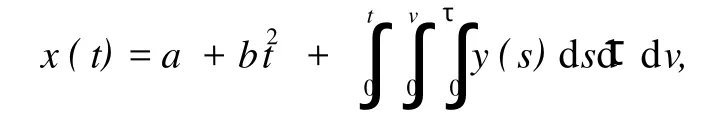
其中,a、b是任意常数,则易知 x(t)是方程 (5)且满足式 (2)的解,从而式 (4)成立。

[1] L IU B ING.Solvability of multi-point boundary value problem at resonance( IV)[J].Appl Math Comput,2003,143(2/3):275-299.

[2] DU ZENGJI,L IN X IAOJIE,GE WEIGAO.On a third-order multi-point boundary value problem at resonance[J].J Math A-nalAppl,2005,302(1):217-229.

[3] 葛渭高.非线性常微分方程边值问题[M].北京:科学出版社,2007:68-226.

[4] L IU B ING,ZHAO ZH ILI ANG.A note onmulti-point boundary value problems[J].NonlinearAnal,2007,67(9):2 680-2 689.

[5] L IU B ING.Periodic solutions of a nonlinear second-order differential equationwith deviating argument[J].MathAnalAppl,2005,309(1):313-321.

[6] BAIZHANB ING,GEWEIGAO,LIWEIGUO.Existence and multiplicity of solutions for four-point boundary value problems at resonance[J].NonlinearAnal,2005,60(6):1 151-1 162.

[7] KOS MATOV N.A multi-point boundary value problem with two critical conditions[J].NonlinearAnal,2006,65(3):622-633.

[8] L IU B ING.Solvability of multi-point boundary value problem at resonance(II)[J].Appl Math Comput,2003,136(2/3):353-377.

[9] 刘丙镯,车晓飞,陈春香.一类三阶微分方程非局部边值问题的可解性[J].黑龙江科技学院学报,2010,20(3):237-242.

(编辑 晁晓筠)

Existence of solutions for third-ordermulti-point boundary value problem s at resonance

WANG Gang, ZHU Sinian, ZHENG Ting
(College of Sciences,China University ofMining&Technology,Xuzhou 221008,China)

O175.8

A

1671-0118(2011)01-0081-04

2010-12-19

王 刚 (1985-),男,安徽省安庆人,硕士,研究方向:微分方程,E-mail:wangg0824@163.com。