深部巷道围岩散热Laplace解析计算

冯 强, 陈 舟

(1.中国矿业大学 力学与建筑工程学院,江苏 徐州 221008;2.华南理工大学 土木与交通学院,广州 510640)

深部巷道围岩散热Laplace解析计算

冯 强1, 陈 舟2

(1.中国矿业大学 力学与建筑工程学院,江苏 徐州 221008;2.华南理工大学 土木与交通学院,广州 510640)

目前矿井建设越来越深,热害给煤矿日常生产带来了严重的影响。针对深埋巷道的特点,将计算模型简化为二维平面圆模型,采用 Laplace变换与逆变换的方法对深埋巷道围岩温度场及散热量进行分析,将时间域上的问题转化为 Laplace域上的问题,得到 Laplace域上的解,再将Laplace域上的解反变换到时间域上;用 Laplace积分逆变换的形式解析表示计算结果。由于计算时间域上的解较困难,需将 Laplace域上的解采用 Stehfest反演方法进行数值逆变换,得到时间域上的数值解答。误差验算表明,当循环级数 N=18时,误差为 10-5～10-7。工程实例也说明此方法的正确性。

围岩温度场;围岩散热量;Laplace变换及逆变换;Stehfest算法;MATLAB

Abstract:This paper is aimed at studying the serious effect of increasingly deeperm ine-induced heat harm on m ining operation.The study consists of simplifying the analyticalmodel into circularity,drawing on the characteristic of deeply buried roadways,analyzing the temperature field and heat radiation by the Laplace transform and the inverse Laplace transform,transform ing the problem from time domain into Laplace domain,developing the Laplace domain solution which is inversely transformed to that in time domain,and finally expressing the computed result by the form of the inverse Laplace transform.The more difficult calculation of the time domain solution necessitates Stehfest inverse transformation ofLaplace domain solution,thus giving the numerical solution in time domain.The error check shows thatwhen the cycle seriesN=18,the error is about 10-5～10-7.The method proves correct.

Key words:temperature field of surrounding rock;surrounding rock heat radiation;Laplace transform and inverse Laplace transform;arithmetic of Stehfest;MATLAB

随着煤炭资源的大量消耗,矿井建设越来越深,井下巷道围岩的温度也越来越高,热害问题日益严重。热害严重影响井下工人的身体健康和矿井的正常生产,已与瓦斯、顶板、粉尘、水、火一同被列为矿井六大灾害。围岩散热是热害最主要的来源[1],了解巷道围岩的温度场分布及围岩散热量有助于采取合理的降温措施。

目前,很多学者对围岩散热现象进行了大量研究,其方法包括有限差分[2]、边界元[3]、有限元[4]、无因次分析。这些研究是基于数值计算而进行的。笔者采用 Laplace解析的方法对围岩散热问题求解[5],得出了较理想的结果。

1 围岩散热问题描述

据深井巷道围岩散热的复杂性,作如下简化:

(1)巷道周围岩体为均质;

(2)巷道截面为圆形;

(3)同一界面上风流温度不随时间变化。

考虑巷道较长、深埋和围岩沿轴线温度梯度较小,该围岩散热计算模型为平面二维模型,见图 1。假设在初始时刻巷道围岩具有相同的温度,即深部地温[6](若初始温度是不均匀的,可类似进行计算)。

图 1 分析模型Fig.1 Analyticalmodel

采用极坐标,巷道围岩热传导问题的控制方程为

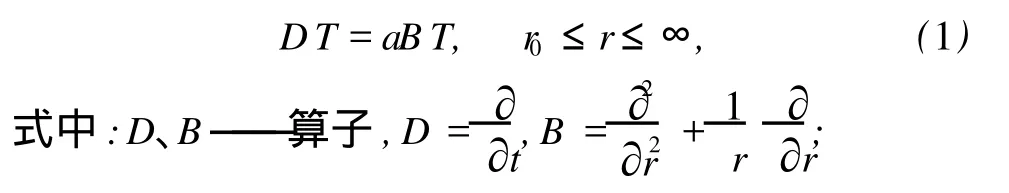
T——径向 r处及 t时刻巷道围岩的温度,℃;

t——时间 (t>0),d;

r——以巷道中心为原点的圆柱坐标,m;

a——热扩散率 ,a=λ/ρc,m2/s;

λ——导热系数,W/(m·K);

ρ——密度,kg/m3;

c——比热容,J/(kg·K)。

问题的边界和初始条件分别为:

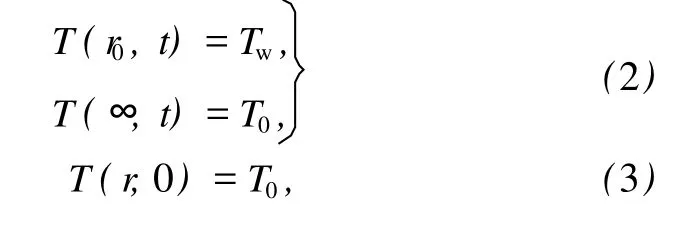
式中:Tw——t时刻巷道表面的气温,℃;T0——围岩的初始温度,℃。

2 Laplace积分变换

围岩温度场的确定采用 Laplace积分变换方法[1]。时间函数 f(t)的 Laplace积分变换 ¯f定义为

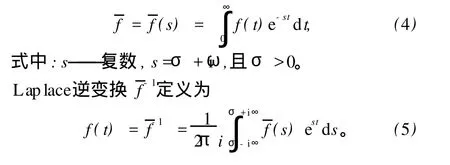
3 热传导问题的求解

为了便于围岩温度场解析计算,将热传导问题作变量替换。取

将变量替换式 (6)分别代入式 (1)、(2)和 (3),热传导问题[7-8]可重新表示为:

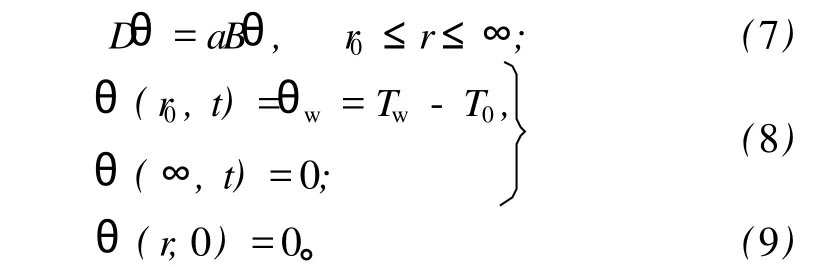
由式 (4)并利用初始条件式 (9),对热传导控制方程式 (7)进行 Laplace积分变换,有

方程式 (10)的解式可表示为

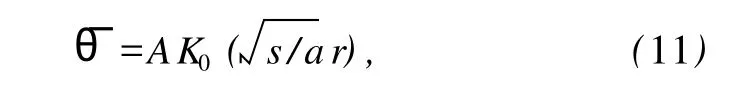
式中:K0(·)——零阶第二类变型 Bessel函数;

A——积分参数,由问题的边界条件确定。

对边界条件 (8)的第一式进行 Laplace变换,并代入式 (11),以确定待定参数 A,再代回,可得

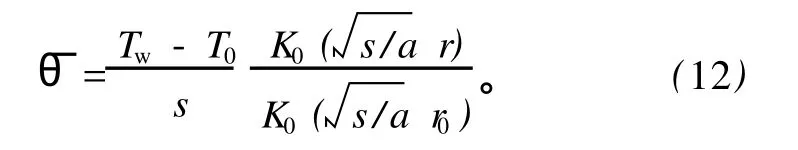
将式 (12)代入 Laplace逆变换式 (5),并代入变量替换式 (6),有

式(13)为围岩温度场的解析算式。将式 (13)对 r进行求导再乘以导热系数λ可得热流密度q,有

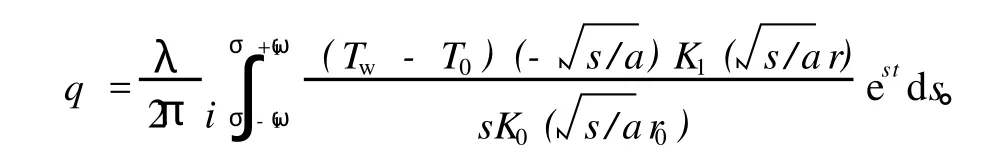
单位长度巷道围岩散热量为

4 Laplace逆变换的数值计算

4.1 误差验算

将式 (14)Laplace域上的解进行逆变换得到时间域上的解较困难,故采用 Stehfest方法[9]对 Laplace逆变换进行数值计算。该算法计算式为

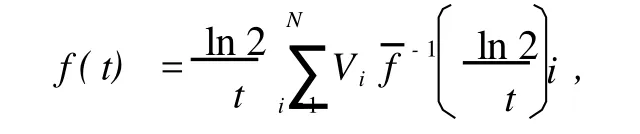
式中 :t——自变量;

N、i、k——正整数;

Vi——中间函数 ,

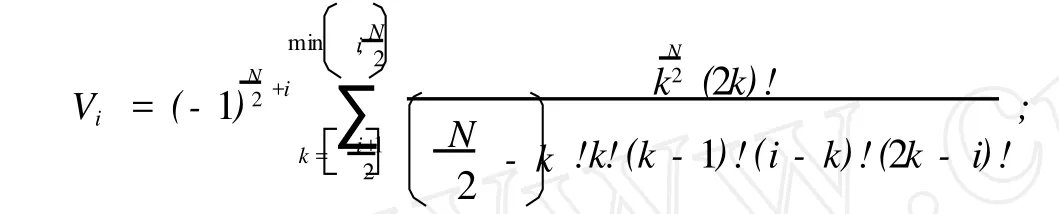
原则上,算法中反演公式项数 N取值越大,计算越精确。下面对该公式的误差进行验算。

误差公式:

误差验算结果如表 1～4所示。

表 1-1(s)=1/s2↔ f(t)=t误差统计Table 1 Error statistics of-1(s)=1/s2↔f(t)=t

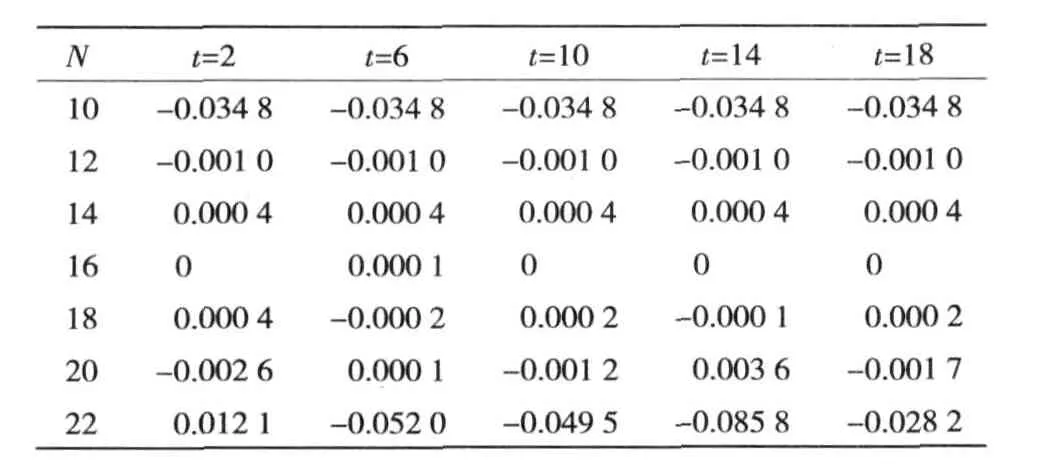
表 1-1(s)=1/s2↔ f(t)=t误差统计Table 1 Error statistics of-1(s)=1/s2↔f(t)=t

?

表 2-1(s)=1/(s2+1) ↔ f(t)=sint误差统计Table 2 Error statistics of-1(s)=1/(s2+1)↔f(t)=sint

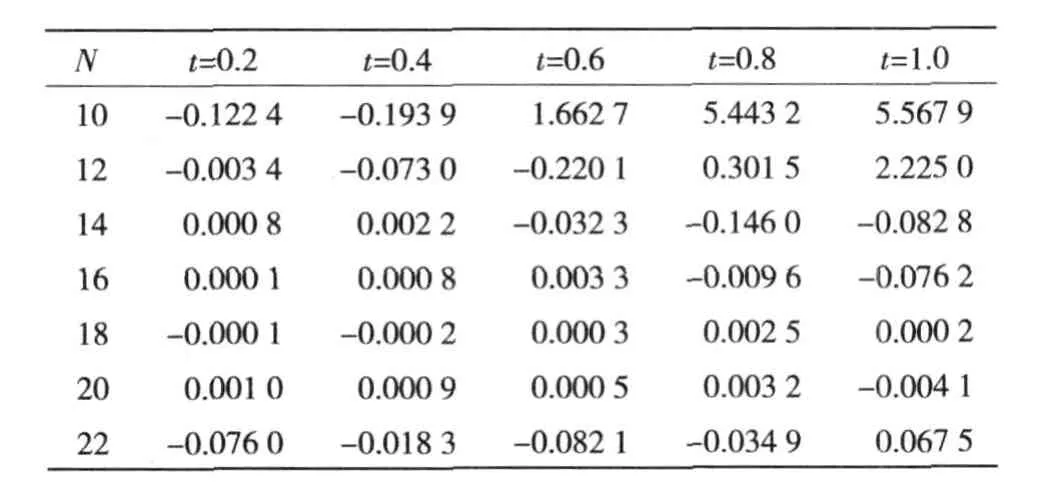
表 2-1(s)=1/(s2+1) ↔ f(t)=sint误差统计Table 2 Error statistics of-1(s)=1/(s2+1)↔f(t)=sint

?

表 3 当 N=18,t>1时-1(s)=1/(s2+1)↔f(t)=sint误差统计Table 3 W henN=18,t>1,error statistics of-1(s)=1/(s2+1) ↔ f(t)=sint

表 3 当 N=18,t>1时-1(s)=1/(s2+1)↔f(t)=sint误差统计Table 3 W henN=18,t>1,error statistics of-1(s)=1/(s2+1) ↔ f(t)=sint

?

从表 2、3中可知,当 0≤t≤1且 14≤N≤22时,误差很小;当 N一定,t继续增大时,误差则急剧增大。

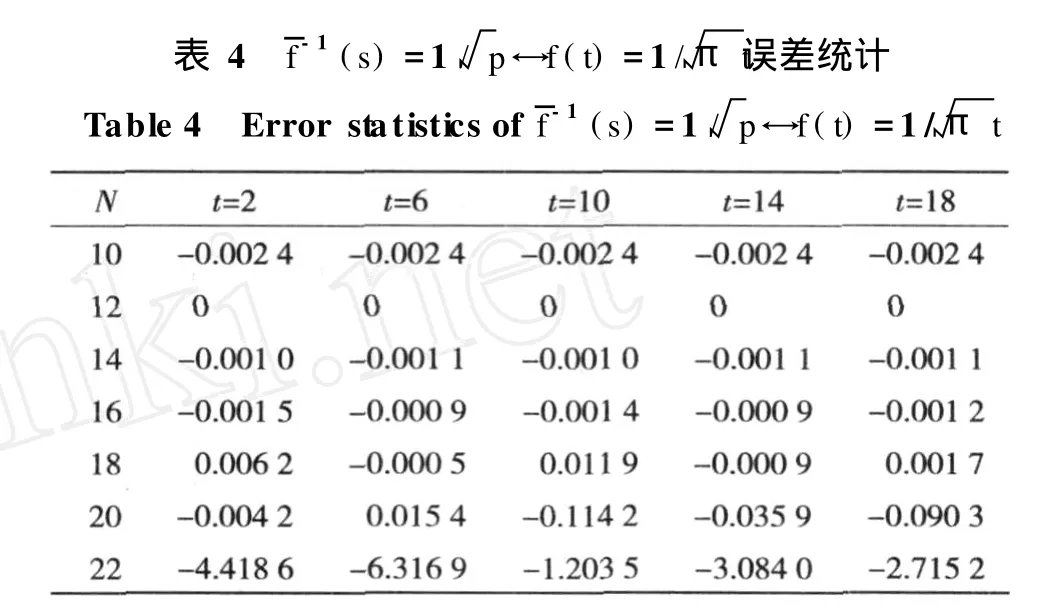
表4-1(s)=1/p↔f(t)=1/πt误差统计Table 4 Error statistics of-1(s)=1/p↔f(t)=1/π t

对比表 1～4可知,当原函数不是周期函数时,此法的误差很小;当 N=18时 Stehfest算法误差最小,达到 10-5～10-7,能满足工程需要。可见,此方法在解答原函数为非周期函数时是正确的。

4.2 工程实例

工程实例[10]为山东新汉矿务局孙村矿。其中,巷道半径为 2.0m,原始岩温为 35.6℃,风温按工作面平均气温取 28.76℃,岩石的导热系数λ为 1.073×10-2W/(m·K),热扩散率 a为 1.174×10-6m2/s。

利用MATLAB编程[11]进行计算,结果见表 5。

表 5 巷道围岩散热量Table 5 Surrounding rock heat rad iation of roadway

由计算结果可知:围岩散热量最大时是刚开挖后的两个月内,随着时间的推移逐渐趋于稳定。该方法能够更清晰地观测围岩散热随时间变化的趋势。

5 结 论

(1)采用Laplace变换及其反变换的方法,建立了深埋巷道围岩散热计算的解析方法,为数值模拟和物理实验提供了理论依据。

(2)深埋巷道围岩温度场及散热量可通过 Laplace逆变换表示。实例计算可知,深埋巷道围岩在前两个月内的散热量占总散热量的绝大部分,随着时间的延长散热量逐渐减小,最终趋于稳定。

(3)误差验算表明,Stehfest方法用于 Laplace的数值反演,可以满足工程需要。

[1] 时 岚,张学博.潮湿巷道围岩散热影响因素的数值分析[J].煤炭科学技术,2009,37(9):51-53.

[2] 高建良,张学博.围岩散热计算及壁面水分蒸发的处理[J].中国安全科学学报,2006,16(9):23-28.

[3] 秦跃平,党海政,刘爱明.用边界单元法求解巷道围岩的散热量[J].中国矿业大学学报,2000,29(4):63-66.

[4] 吴 强,秦跃平,郭 亮,等.巷道围岩非稳态温度场有限元分析[J].辽宁工程技术大学学报,2002,21(5):604-607.

[5] 王照亮,张克舫,李华玉,等.一种求解复合圆筒壁非稳态导热问题的新方法[J].石油大学学报:自然科学版,2005,29(2):89-92.

[6] 蒋斌松,王金鸽,周国庆.单管冻结温度场解析计算[J].中国矿业大学学报,2009,38(4):463-466.

[7] 谢鸿政,杨枫林.数学物理方程[M].北京:科学出版社,2008.

[8] 于 涛.数学物理方程与特殊函数[M].北京:科学出版社,2008.

[9] 刘利强.拉普拉斯反变换的一种数值算法[J].内蒙古工业大学学报:自然科学版,2002,21(1):47-49.

[10] 秦跃平,秦凤华,于明学.用有限单元法研究回采工作面围岩散热[J].辽宁工程技术大学学报:自然科学版,1999,8(4):342-346.

[11] 刘卫国.MATLAB程序设计与应用[M].北京:高等教育出版社,2006.

(编辑 晁晓筠)

Analytical calculation of surrounding rock heat radiation of deeply buried roadway

FENG Q iang1, CHEN Zhou2
(1.Shool ofMechanics&Civil Engineering,China University ofMining&Technology,Xuzhou 221008,China;2.School of Civil Engineering&Transportation,South China University of Technology,Guangzhou 510640,China)

TD727

A

1671-0118(2011)01-0044-04

2010-11-23

冯 强 (1985-),男,山东省威海人,硕士,研究方向:岩石力学理论及其应用,E-mail:fengqiang889966@126.com。