工业机器人最优轨迹规划算法

赵振民, 刘 锋, 孔民秀, 孙立宁

(1.哈尔滨工业大学 机器人与系统国家重点实验室,哈尔滨 150080;2.黑龙江科技学院 电气与信息工程学院,哈尔滨 150027)

工业机器人最优轨迹规划算法

赵振民1,2, 刘 锋2, 孔民秀1, 孙立宁1

(1.哈尔滨工业大学 机器人与系统国家重点实验室,哈尔滨 150080;2.黑龙江科技学院 电气与信息工程学院,哈尔滨 150027)

为优化机器人的工作性能,在分析工业并联机器人工作特性的基础上,将执行时间最优、跃度最小、能量最小、运动学和动力学约束为目标函数,应用惩罚函数法并加入初始速度、加速度、跃度和力矩约束,且目标约束条件中加入谐振频率限制,依据所建立的目标函数进行了遗传算法优化求解,对所得结果进行了三次样条插值,并在一台三自由度的工业搬运并联机械手上进行了实验。结果表明,在保证工作效率和节约能量的条件下,该轨迹规划方法可以减少机械部分的跃度,避免机械部分的谐振,降低机械和电机的磨损。

并联工业搬运机器人;轨迹规划;三次样条插值;遗传算法;截止频率约束

Abstract:This paper is a study on opt imizing the performance of the robot.The study consistsof analyzing the operating characteristics of industrial robots,employing the optimal execution time,minimum jerk,minimum energy,and the kinematics and dynamics constraints as objective function,applying penalty function method to achieve the initial velocity,acceleration,jerk and torque constraints,adding the resonant frequency restrictions to target constraints,developing the genetic algorithm optimization of the established objective function,performing cubic spline interpolation of results,and conducting an experiment on a three degree of freedom parallelmechanical handling industry hands.The results show that the planningmethod can ensure energy efficiency and conservation while reducing the mechanical parts under jump,avoiding the mechanical part of the resonance,and reducing the mechanical and electricalwear.

Key words:parallel industrial handing robot;trajectory planning;cubic spline interpolation;genetic algorithms;cut-off frequency constraints

对工业机器人的轨迹进行规划算法研究,可以优化机器人的工作性能,降低设备的磨损程度,提高工作效率和延长设备的使用期限。在近十年中,机器人的轨迹规划获得极大的发展,诸如时间最优轨迹规划 (t ime optimal trajectory planning,TOTP)、能力最优轨迹规划 (minimum energy trajectory planning,METP)、跃度有界的轨迹规划 (minimum jerk trajectory planning,MJTP)以及合成最优轨迹规划 (synthetic optimal trajectory planning,SOTP)等[1-3]。笔者分析研究了文献[4-14]众多的规划算法,在总结优劣的基础上,结合工业并联机器人的工作特性,将时间、跃度以及能量联合,建立优化的目标方程,应用加入了惩罚条件的遗传算法对所建立的目标函数进行优化,对位置给定信号按照优化的时间间隔用三次样条插值进行插值计算,并且在一台完全具有自主知识产权的工业搬运机器人上验证所规划的轨迹。

1 目标函数的确定

将操作转换到关节空间中进行轨迹规划,这样做的好处,其一是避免了运动学奇异性和机械手臂的冗余,其二是控制力作用在关节上,而不是作用在末端,因此可以很简单地判断所设计的轨迹是否和关节空间对应。它的主要缺点是当将关节空间通过正动力学映射到末端时不容易预见末端的实际运动[5]。实验验证轨迹规划算法的机器人如图 1所示。

图 1 三自由度工业搬运机器人Fig.1 Three-d imensionalmodel of industrial handl ing robot

该机器人的两个关节端装配了多摩川的绝对式光电编码器,完成控制上的位置反馈以及末端的位置策略。由于课题中的机器人只有两个轴是耦合的,第三个轴和上面两个耦合轴之间是完全解耦的,所以这里只对该机器人的两个耦合轴进行优化。

在工业生产中,效率是很重要的因素,因此,在目标函数中,时间的最小化是必须加入的优化目标。对跃度限制的原因是,高的跃度能增加机械磨损,破坏机械结构,增加谐振频率,而且非平滑轨迹会导致电机损坏,增加轨迹跟踪误差。由于电机的基本结构是线圈,它的电流是连续的,电压是有界的,电机的电流则直接对应着电机的力矩输出,因此,电机不能产生非连续性的力矩。当所规划的轨迹出现非连续性力矩时,电机对整个机械系统将产生很大的高频机械振动,机械机构将遭到破坏,电机磨损增加。工业机器人的工作特性一般都是重复性的操作,因而要对每个关节的能量提出要求,这样可以避免运行过程中单个电机过热而烧毁。将系统能量用动力学方程的计算力矩的平方和来刻画,则整个系统的目标函数为

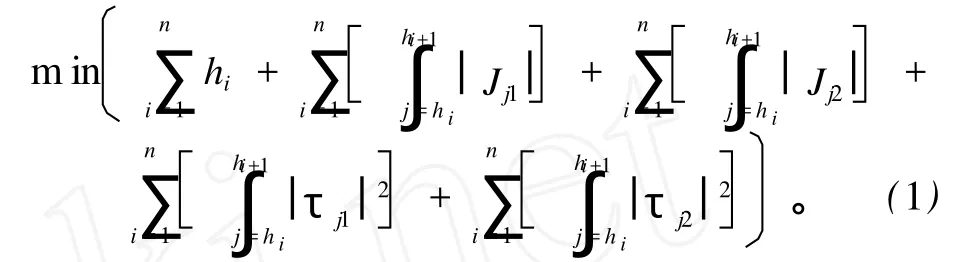
式 (1)中第一项表示时间间隔,以此来提高机器人的生产效率。第二、三项分别为两个轴跃度函数,用以减少机械部分的磨损。第四、五项分别表示两个轴能量函数,目标是达到最大的能量节约和防止单个电机过热引起损坏。

约束条件为:

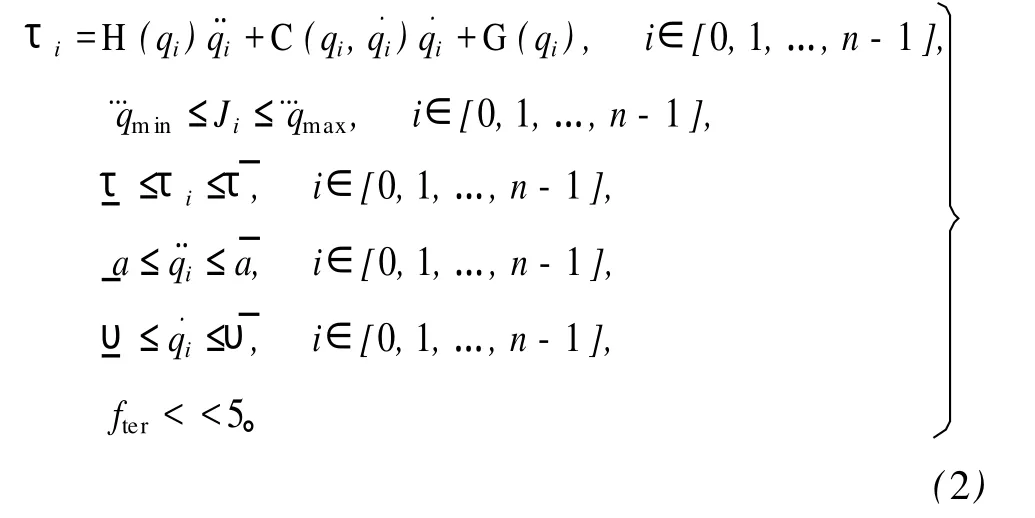
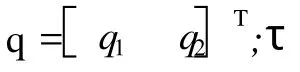
其他的机器人的关节的速度和加速度可以通过三次样条曲线插值中的参数确定,不再详述。fter为给定的位置信号的截止频率,已知机械系统的谐振频率为 5 Hz,为避免所给定的插值之后的位置信号的频率分量在机械谐振频率内引起机械谐振,对给定插值之后的位置信号的截止频率进行了限制。

2 目标函数的优化算法

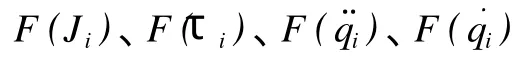
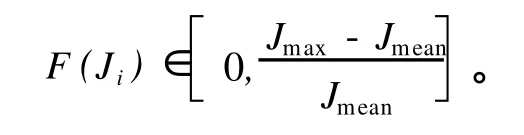
式 (4)中τi是力矩幅值,τmean是力矩幅值的指标值,

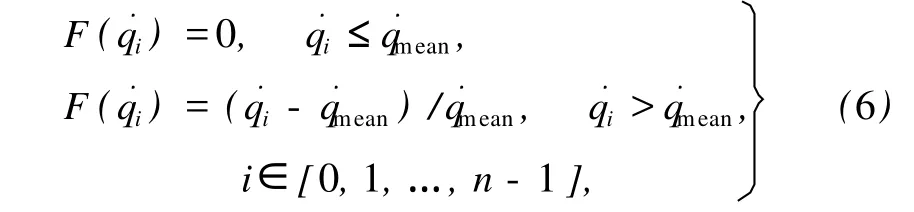
式(6)中˙qi是速度幅值,˙qmean是速度幅值的指标值,

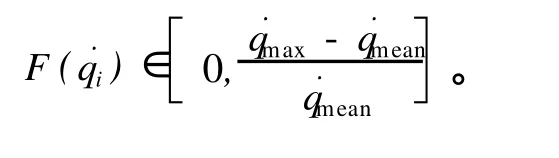
当满足上述约束条件时,函数值为零;当点在可行域之外时,对目标函数值加以惩罚。

文中还引入参数 R1、R2、R3、R4进行归一化处理,其分别为跃度、力矩、加速度和速度的归一化转化系数,使 RiF(·)在 (0,1)范围内。这样易于比较目标函数中各项之间的权重。其中,

为体现惩罚程度,引入四个惩罚因子 Q1、Q2、Q3、Q4,通过较大的权重系数体现惩罚程度,从而使得跃度、力矩、加速度、速度变化影响作用较小。综上,得到的不等式约束条件的惩罚项为

总体的目标函数为:

式 (7)中,Qi(i∈[1,2,…,9])为惩罚因子,可以通过条件惩罚因子获得不同约束量对整个目标函数的贡献。

在优化过程中,为避免非可行点影响优化过程,需要将非可行点转化为可行点。采用 FSC法[15]定义的调整系数如下:

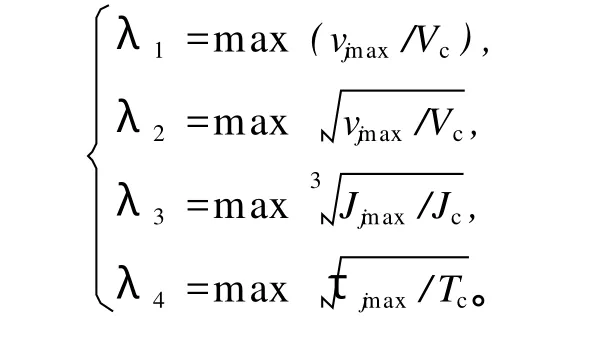
λ=max(1,λ1,λ2,λ3,λ4),j=1,2。若λ =1,则该点为可行点,无须转化;若λ>1,则应将 hi增加到λhi(i=1,2,…,n-1),以使其成为可行点。

3 结果分析

采用惩罚性的遗传算法,对目标函数进行优化计算,优化结果见图 2。得到最优的目标函数值为992 115.279 161 772 2,计算的代数为 72代。

图 2 遗传算法的优化结果Fig.2 Results of genetic algorithm opt im ization

优化结果所产生的时间间隔数据采用三次样条插值,对给定的数据点之间的值进行数据密化,处理后的机械手臂的关节位置如图 3所示,机器人关节响应速度、加速度和跃度见图 4,关节插值轨迹的频谱分布见图 5。

图 3 三次样条轨迹规划后的机器人关节位置Fig.3 Robot joint by three orders after spine trajectory plann ing

课题中的工业机器人的机械谐振频率在 5 Hz附加,通过上述对比可以发现,采用三次样条插值所产生的位置给定信号的截止频率均远小于 5 Hz,因此,说明该种轨迹规划算法可以很好的降低给定信号的截止频率。

4 结束语

笔者通过对并联机械手臂运动学、动力学和频率点约束,建立了以执行时间、跃度和电机功率为目标函数的轨迹规划的优化目标函数,应用惩罚条件对目标函数进行遗传算法求解,对得到的结果进行三次样条插值,并在三自由度的工业搬运机器人上进行了实验。该轨迹规划可以使给定信号的截止频率小于机械的谐振频率,并且可在提高工作效率的条件下降低机械部分的冲击,减小电机和机械部分的磨损。

[1] GASPARETTO A,ZANOTTO V.A technique for time-jerk optimal planning of robot trajectories[J].Robotics Computer-IntegratedManufacturing,2008,24(3):415-426.

[2] DONG J Y,FERRERRA PM,STOR IJ A,Feed-rate optimization with jerk constraints for generating minimum-time trajectories[J]. International Journal of Machine Tools and Manufacture,2007,47(12/13):1 941-1 955.

[3] KAHN M E,BOTH B.The nearminimum-time control of open loop articulated kinematic chains[J].Journal of Dynamic Systems,Measurement,and Control,1971,93(3):164-172.

[4] DIEDERIKVERSCHEURE,BRAM DEMEULENAERE,JAN S WEVERS,et al.Time-optimalpath tracking for robots:a convexoptimization approach[J].IEEE Transactions on Automatic Control,2009,54(10):2 318-2 327.

[5] ALESSANDRO GASPARETTO,VANNI ZANOTTO.A technique for time-jerk optimal planning of robot trajectories[J].Robotics and Computer-Integrated Manufacturing,2008,24(3):415-426.

[6] CHEN Y C.Solving robot trajectory planning problems with uniform cubic B-splines[J].Optimal Control ApplMethods,1991,12(4):247-262.

[7] MACHFARLANE S,CROFT EA.Design ofJerk bouned trajectories for on-line industrial robot applications[C]//Proceedings of the 2001 IEEE InternatinalConference on Robotics&Automation.Seoul:[s.n.],2001.

[8] CRA IG J J.Introduction to Robotics[M].2nd ed.New York:Addison-Wesley,1989.

[9] JEON J W.An efficient acceleration for fast motion of industrial robots[C]∥Pro 1995 IEEE Int Conf Ind Elec,Cont&Instr.Orlando:[s.n.],1995:1 336-1 341.

[10] KYR IAKOPOULOS K J,SAR ID IS G N.M inimum Jerk path generation[C]∥Proc 1988 IEEE Int Conf Rob&Aut,Philadelphia:[s.n.],1988:364-369.

[11] P IAZZIA,V IS IOL A.Golbal minimum-jerk trajectory planning of robotmanipulators[J].IEEE Trans Ind Elec,2000,47(1):140-149.

[12] MACFARLANE S,CROFT EA.Jerk-boundedmanipulator trajectoryplanning:design for real-t ime applications[J].IEEE Transactions of on Robotics and Automation,2003,19(1):42-52.

[13] CONGM ING,XU X IAOFEI,XU PETER.Time-jerk synthetic optimal trajectory planning of robot based on fuzzy genetic alorithm[C]//15th International Conference on Mechatronics and Machine Vision in Practice(M2V IP08).Auckland:[s.n.],2008:2-4.

[14] GASPARETTO A,ZANOTTO V.Optimal trajectory planning for industrial robots[J].Advances in Engineering Software,2010,41(4):548-556.

[15] ORVOSH D,DAVIS L.Using a genetic algorithm to optimize problems with feasibility constraints[C]//Proceedings of the First IEEE Conference on Evolutionary Computation. Fogel:[s.n.],1994:548-552.

(编辑 徐 岩)

Industrial robot opt imal trajectory planning algorithm

ZHAO Zhenm in1,2, LIU Feng2, KONG M inxiu1, SUN L ining1
(1.State KeyLaboratory of Robotics&System,Harbin Institute of Technology,Harbin 150080,China;2.College of Electric&Information Engineering,Heilongjiang Institute of Science&Technology,Harbin 150027,China)

TP242.2

A

1671-0118(2011)01-0069-05

2010-08-30

国家高技术研究发展计划(863计划)项目(2006AA040103)

赵振民 (1967-),男,黑龙江省双城人,教授,博士研究生,研究方向:机器人控制、高频功率变换、软开关技术,E-mail:ycxh101-cc@126.com。