高中数学中不等式的证明方法
2011-09-21 06:27:46苟一泉赵中玲
时代农机 2011年7期
黄 东,苟一泉,赵中玲
(西南大学 数学与统计学院,重庆 400715)
1 三角代换
利用三角函数进行换元,把一般不等转化为三角函数问题,实现了问题化归解决的目的)
例 1:已知:x2+y2≤1,求证:
2 换元法
引进新的变元,转化解决问题的角度。
3 反证法
当正面研究问题有困难时,常常换一种思路,从其反面着手,往往会化难为易。
例 3:坌a,b,c缀(0,1),求证:(1-a)b,(1-b)c,(1-c)中至少有一个不大于
4 放缩法
利用常见不等式进行适当的放大或者缩小,以达到证题的目的。
例 4:已知 a,b,c缀R+, 求证:

由(1),(2),(3)得:
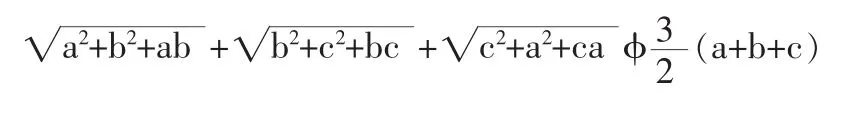
5 判别式法
把复杂的不等式问题转化为熟悉的一元二次函数问题,达到简化的目的。
6 构造法
构造合适的数学情景,如:函数,图形等,利用熟知的知识来解决抽象的不等式问题。
证明:构造△ABC,O 为其内一点,且有 AO=x,BO=y,CO=,由余弦定理知:
7 向量法
利用向量的手段,把代数问题向量化,转化了思考问题的角度,拓宽了思路。
此外,不等式的证明方法还有:Cauchy不等式,排序不等式,函数的凹凸性,数学归纳法等,限于篇幅,这里就不再赘述。不等式是高中数学的重点与难点,笔者对不等式的证明方法作了一些总结,希望能为读者在认知不等式的过程中提供思路。
猜你喜欢
新高考·高一数学(2022年3期)2022-04-28 07:02:46
小学生学习指导(低年级)(2021年3期)2021-07-21 03:02:36
中学生数理化(高中版.高考数学)(2021年1期)2021-03-19 08:28:36
中学生数理化(高中版.高二数学)(2020年11期)2020-12-14 07:36:32
中学生数理化(高中版.高考数学)(2020年10期)2020-10-27 03:04:28
河北理科教学研究(2020年1期)2020-07-24 08:14:28
小学生学习指导(低年级)(2018年3期)2018-01-31 02:18:59
数学小灵通(1-2年级)(2017年10期)2017-11-08 08:39:18
智富时代(2017年4期)2017-04-27 02:13:48
高中生学习·高三版(2016年9期)2016-05-14 09:12:05

