颗粒材料数值样本的坐标排序生成技术
楚锡华
(1. 武汉大学 工程力学系,武汉 430072;2. 武汉大学 水资源与水电工程科学国家重点实验室,武汉 430072)
1 引 言
颗粒材料的宏观性质与其微观结构(颗粒形状、粒度分布以及配位数等)密切相关,特别是颗粒材料的孔隙度,或者说结构密度关系到颗粒材料的诸多性质,如力学响应、渗透性、溶解质和热量的扩散性能等。因此,Herrmann[1]认为,结构密度是描述颗粒系统行为的最重要参数,它实际上控制了颗粒材料的力学行为。孔隙度是颗粒集合中孔隙体积与颗粒集合总体积的比值,在二维情况下,孔隙度是孔隙面积与颗粒集合总面积的比值。它是颗粒材料的宏观参数,表征了颗粒材料的相对密度。与其相应的微观参数是颗粒材料的平均配位数(average coordinate number)。一个颗粒的配位数是指与之相接触的颗粒的个数(主要是针对圆形颗粒或椭圆形颗粒定义的参数),平均配位数是指颗粒集合内所有颗粒配位数的算术平均值。孔隙度与颗粒材料的颗粒形状、粒度分布及排列方式等有密切的关系。显然颗粒材料的孔隙度不能任意取值,对特定粒度分布的颗粒材料,一方面在颗粒相互不重合的情况下孔隙度有一个下限值,如对单粒度圆形颗粒(二维情况)组成的颗粒集合,其孔隙度最小值为0.093 1,单粒度球形颗粒(三维)组成的颗粒集合,其最小孔隙度为0.259 5;另一方面,虽然颗粒材料的孔隙度理论上可趋近于 1,但颗粒稀疏到一定程度后,颗粒之间将不接触,此时颗粒集合的平均配位数将趋于0,颗粒集合失去承载能力。
此外,以离散颗粒模型研究岩土颗粒材料时,由于不同类型的岩土材料在孔隙度以及粒度分布上存在一定的差别,为了更真实地模拟不同岩土材料的力学行为,在数值模拟时有必要研究颗粒材料的随机生成技术,以使生成的颗粒材料数值样本具有相应的孔隙度及粒度分布。因此,颗粒材料数值样本生成及颗粒排列技术日益受到重视[2-8],研究者提出了多种样本生成方案,然而至今仍无一条公认的优化途径[7]。文献[2]指出,生成颗粒材料的困难在于随机生成时布点的分散性和生成的颗粒材料的真实性。魏群[9]基于RSA模型给出了随机布点及挑选满足要求的颗粒的方法。本文在此基础上改进了其随机布点方式,即先通过对随机生成的x坐标序列或y坐标序列进行排序,然后再形成坐标对进行布点,从而使在给定的区域内能够生成更多符合要求的颗粒。
2 颗粒材料数值样本生成的RSA模型
2.1 经典RSA模型
RSA模型也称为 SSI模型(simple sequential inhibition model)。其主要思想如下:首先按粒度分布要求生成备选粒径序列{ri},然后在给定二维或者三维区域内按照随机方式逐一给定r1,r2......的中心位置设当前颗粒为i,若颗粒i与已存在的颗粒重合,则将i舍弃,继续用i+1试探,该过程直至给定区域填充满,亦即任何颗粒无法放入该区域为止。为简便起见,以二维为例,在所考虑区域Ω内随机布点i( xi,yi),且满足如下条件 xi⊂[Xmin,Xmax]yi⊂[Ymin, Ymax],其中Xmin、Xmax、Ymin、Ymax为区域Ω最小外接矩形的角点坐标值。xi,yi通常以随机数列的方式给出,即
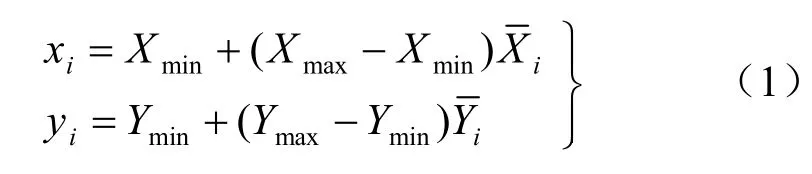
2.2 RSA模型的若干改进
经典RSA模型虽然简单,但只能生成非常稀疏的颗粒集合体,一旦要求生成的颗粒体的孔隙度较小时,会造成相当多的颗粒因重叠而被舍弃,使得颗粒集合的粒度分布与目标粒度分布往往有较大的差异(主要是由于在生成非单粒度颗粒群的过程中,较小的颗粒总有较多的机会在给定区域内找到位置)。为此,在应用时需对RSA模型进行改进。
(1)改进方案1
该改进方案主要针对当前颗粒i与已生成的颗粒存在一定重叠时,并不直接舍弃颗粒i,而是根据重叠量作如下处理:
设与其重叠的颗粒为a,其半径为ra,坐标为重叠量为Δ,则存在如下关系
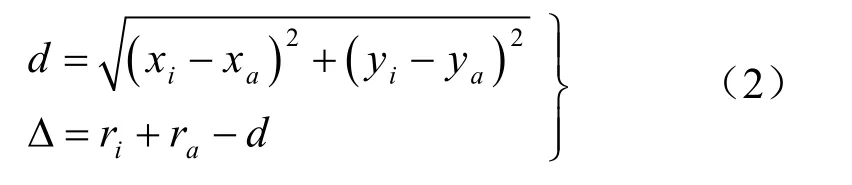
式中:d为两颗粒中心之间的距离,颗粒i的坐标按如下方式修正
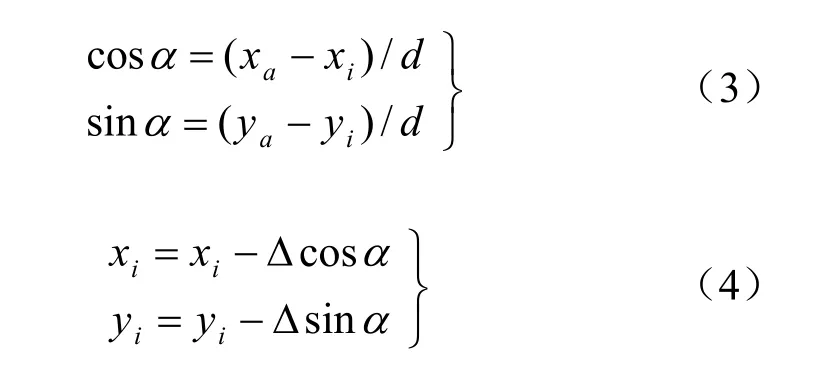
应用新的坐标判断颗粒i是否与已存在的颗粒重叠,若不重叠,则保留该颗粒,否则,继续修正,若修正k次后,仍与已存在的颗粒重叠,则舍弃该颗粒。
(2)改进方案2
该改进模型为:若当前颗粒i与已生成颗粒重叠时,仅仅舍弃坐标而保留ri,并将以ri为半径,以坐标为圆心的颗粒视为当前颗粒。从理论上看,这一方案能较好地维持粒度分布的要求,但要求备选的坐标序列要远远大于目标颗粒数目。若将能够得以保留的坐标称为存活坐标,将存活坐标的数目与备选坐标的数目之比称为坐标存活率,则上述改进方案的坐标存活率很低。对同一粒度序列,不难理解对备选坐标数目相同的坐标序列,坐标存活率的提高在某种程度上可使生成密实颗粒集合的可能性更大。这是由于当坐标存活率较低时,往往会发生粒度序列仍未循环结束,而备选坐标序列已用完,但此时生成的颗粒数目仍未满足要求,因而在商用颗粒流软件 PFC2D中,若保持粒度大小不变的情况下常会发生无法生成目标颗粒数目的情况。
(3)改进方案3
该方案在方案1与方案2的基础上,若颗粒重叠时,并不直接舍弃当前坐标,而是根据重叠量应用方案1调整当前颗粒的坐标,若调整k次后,仍与已存在的颗粒重叠,则保留半径ri,重新选择下一个随机坐标,该方案得到的样本一般仍比较松散。
(4)改进方案4
增加生成颗粒数目的一种最直接的方式是增大粒度序列与坐标序列。但在这里笔者将寻求另外一种方式,即保持现有粒度序列与坐标序列大小不变的情况下,如何提高生成颗粒的数量。注意到经典RSA模型及改进方案2中对坐标序列及种子序列的编号是随机数列进行的,为了简单起见,假定粒度序列为等粒度序列,由于对颗粒的挑选是按照编号进行的,则可能会出现图 1(a)所示的情况,在这种情况下,颗粒1首先生成,那么颗粒2(坐标2)和颗粒3(坐标3)都将因为和颗粒1重叠而被舍弃。但如果将图1(a)的3个坐标序列排序后按照图1(b)进行编号,那么只有颗粒2因重叠被舍弃,从而提高坐标的存活率,因此,首先对进行排序,然后再形成坐标序列( xi, yi),结合经典的RSA模型可称为改进方案4a,结合改进方案1称为改进方案4b,结合改进方案2称为改进方案4c,结合改进方案3成为4d。下面将以一个简单的算例来说明经过坐标排序后的方案能够生成更多的颗粒。
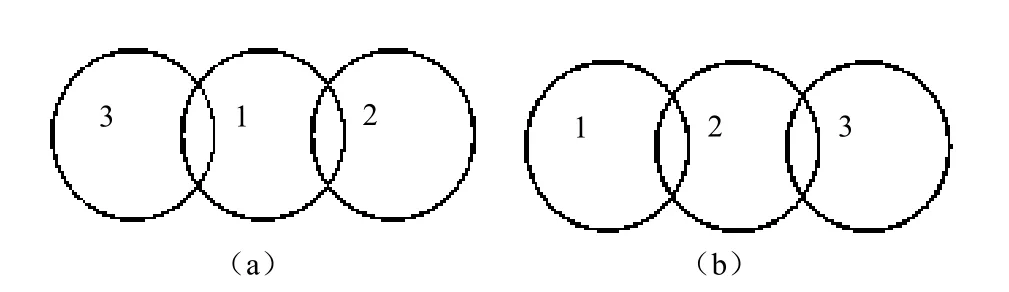
图1 颗粒随机生成示意图Fig.1 Diagram of random packing
3 数值算例
在宽为20 cm、高为40 cm的矩形区域内生成半径为0.3、0.4、0.5 cm的颗粒集合(其颗粒数量之比为 4:3:3)。其中,随机数列采用混同余法,其递推公式可表示为

式中:{ri}为待生成的随机数列;通常选取D为正奇数; M=2k; C=4q+ 1;X0为任意非负整数,通常随机数列的种子,在本算例中 D= 13 849,C=2 053,M= 65 536。的种子为20 001,的种子为60 001。表1给出了采用不同方案时,生成的颗粒总数量随粒度序列的变化,为了简便起见,这里取粒度序列的大小与坐标序列相等。表1中N表示粒度序列(坐标序列)的大小,从表可以看出,各个方案随粒度序列(坐标序列)的增大,生成的颗粒数目在递增。对比各个方案可看出改进后的方案均优于经典RSA模型,包含坐标修正的方案优于不包含修正的方案,即方案1、方案3优于方案2,方案4b与方案4d优于4a及4c。并且经过坐标排序的方案均优于与其对应的未经排序的方案,即方案4a优于经典RSA,方案4b优于方案1,方案4c优于方案2,方案4d优于方案3。
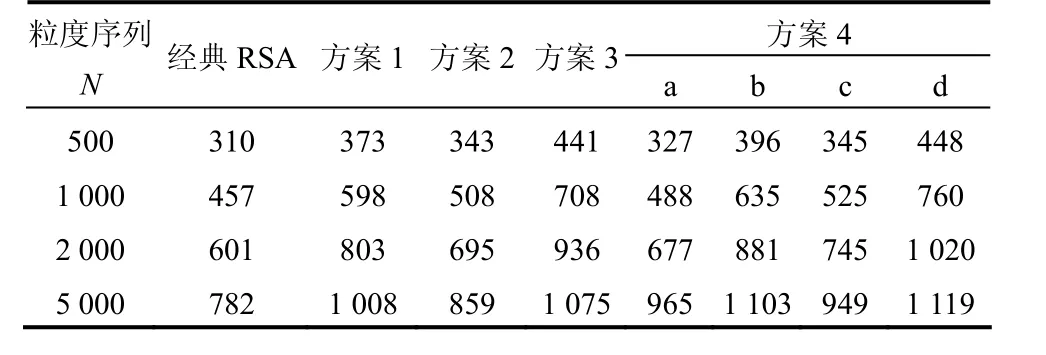
表1 各个RSA模型生成颗粒数量的对比Table 1 Comparison of number of grains generated by different RSA methods
下面将着重探讨当N =5 000时生成颗粒数在1 000以上的3种方案,即方案1、方案3、方案4b及4d。图2(a)~(d)给出了其对应生成的颗粒集合,统计可知,其生成的半径为0.3、0.4、0.5 cm的颗粒的数量之比分别为(547:271:190);(505:306:264);(521:314:268);(453:339:327),对比可看出,方案4d生成的颗粒级配最接近要求的级配(4:3:3)。下面从生成的颗粒集合的接触分布探讨颗粒集合的各向异性情况,图3给出了方案1、方案3、方案4b及方案4d生成的颗粒集合的接触法向分布。
可以看到未经坐标排序的方案生成的颗粒集合较接近各向同性,而以x坐标排序的方案生成的颗粒集合在x方向上的接触较为密集。对圆形颗粒集,在理论上接触分布应是关于原点对称的,但对稀疏颗粒集合接触统计时误差的影响比较显著,因此,图 3(a),3(b)在一定程度上丧失了对称性。此外,需指出坐标排序方案虽然能生成较多的颗粒,但通常其颗粒集合的密实程度仍不能满足颗粒材料二维离散单元数值模拟的样本要求,如方案4 d虽生成了1 119个颗粒,但此时的孔隙度为0.305,颗粒的平均配位数(接触点个数)为1.89。通常而言,RSA模型可通过颗粒膨胀并结合颗粒样本生成的动力方案[8],从而使颗粒材料样本达到离散单元数值模拟的要求。

图2 不同方案生成颗粒集合Fig.2 Granular assemblies generated by different methods
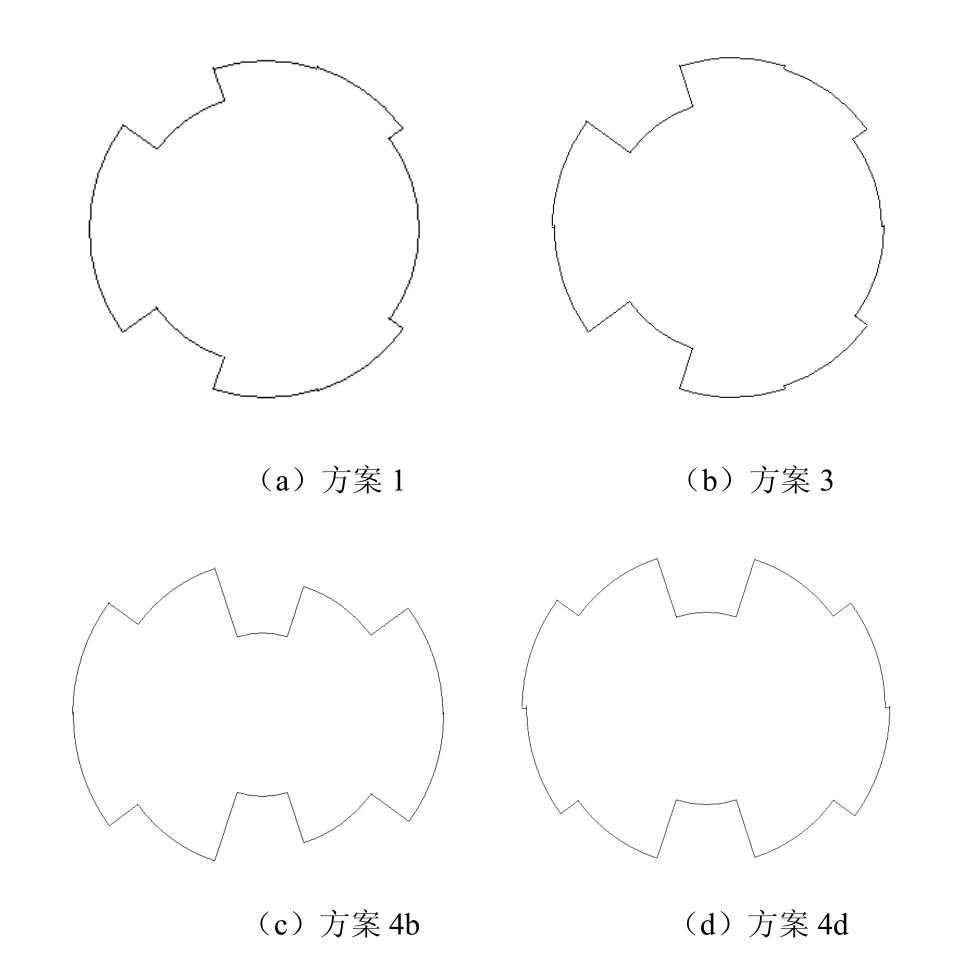
图3 不同方案生成的颗粒集合的接触法向分布图Fig.3 Distributions of contact normals of granular assemblies generated by different methods
4 结论与评述
(1)本文在颗粒材料数值样本生成的经典RSA模型基础上,讨论了几种修正方案,并建议了一种基于坐标排序的样本生成技术。数值算例表明,坐标序列经过排序后,再结合相应的RSA模型能够在一定程度上提高坐标序列的存活率,从而使生成的颗粒集合趋于密实。坐标排序属于坐标序列的规则化,这与 Sobolev[10]所建议的技术在一定程度上相类似。需要指出,颗粒的规则排列及随机排列技术,特别是如何随机排列使生成的颗粒材料趋于更密实,至今仍是一个活跃的课题[11-12]。本文仅以RSA模型为基础从几何构造的角度进行了初步的探讨。文中所给例题虽为二维算例,但该方法不难推广至三维情况。
(2)目前颗粒材料数值样本的生成方法还处在百家争鸣的阶段,总体而言,可分为动力方法与构造方法[4-8]。构造方法在生成样本过程中不涉及颗粒的物性,因此,所生成的初始数值样本可用于模拟不同物性的颗粒材料;动力方法在生成样本的过程中需用到颗粒间的相互物理作用,所生成的颗粒样本与颗粒间的相互作用密切相关。此外,需特别值得关注的是,基于网格的颗粒样本几何构造算法[7-13]因能较好地应用有限单元法的网格剖分技术而具有一定的优势。
(3)颗粒材料数值样本生成问题本质上属于颗粒排列堆积问题。颗粒排列特别是圆形(球形)颗粒的排列问题在学术(包括数学,物理、材料,岩土、化工等领域)及工业应用中都具有重要的意义,因而成为经久不衰的研究主题[1-17]。经典颗粒排列问题主要关心在不同形状的容器内如何用等尺寸圆盘得到最致密排列。此外比较关注生成结构的几何性质,如颗粒尺寸分布与指定尺寸分布的一致性、接触的各向同性特性、配位数等。对颗粒材料数值样本的要求及各类生成技术的详细比较笔者将在另文表述。
[1]HERRMANN H J. Granular matter[J]. Physical A., 2003,313: 188-210.
[2]LAURENT T, PIERRE P, AURELE P. Generation of granular media[J]. Transport in Porous Media, 1997, 26:99-107.
[3]WANG C Y, VEI CHUNG L. A packing generation scheme for the granular assemblies with planar elliptical particles[J]. Int. J. Numer. Anal. Methods Geomech.,1997, 21: 327-358.
[4]CHENG Y F, GUO S J, LAI H Y. Dynamic simulation of random packing of spherical particles[J]. Powder Technology, 2000, 107: 123-130.
[5]FENG Y T, HAN K, OWEN D R J. Filling domains with disks: An advancing front approach[J]. Int. J. Numer.Meth. Engng., 2003, 56: 699-713.
[6]JIANG M J, KONRAD J M, LEROUEI S. An efficient technique for generating homogenous specimens for DEM studies[J]. Computers and Geotechnics, 2003,30(7): 579-597.
[7]CUI L, SULLIVAN O. Analysis of a triangulation based approach for specimen generation for discrete element simulations[J]. Granular Matter, 2003, 5: 135-145.
[8]BAGI K. An algorithm to generate random dense arrangements for discrete element simulations of granular assemblies[J]. Granular Matter, 2005, 7(1): 31-43.
[9]魏群. 岩土工程中散体单元的基本原理、数值方法及实验研究[D]. 北京: 清华大学, 1990.
[10]SOBOLEV K, AMIRJANOV A. A simulation model of the dense packing of particulate materials[J]. Advanced Powder Technology, 2004, 15(3): 365-376.
[11]TORQUATO S, TRUSKETT T M, DEBENEDETTI P G.Is random close packing of spheres well defined?[J].Physical Review Letters, 2000, 84(10): 2064-2067.
[12]ZAMPONI F. Packings close and loose[J]. Nature, 2008,53: 606-607.
[13]JERIER J F, RICHEFEU V, IMBAULT D, et al. Packing spherical discrete elements for large scale simulations[J].Computer Methods in Applied Mechanics and Engineering, 2010, 199: 1668-1676.
[14]SCOTT G D. Packing of spheres[J]. Nature, 1960, 188:908-909.
[15]ZASKI A M. An efficient method for packing polygonal domains with disks for 2D discrete element simulation[J].Computers and Geotechnics, 2009, 36(4): 568-576.
[16]HERN C S, LANGER S A, LIU A J, et al. Random packing of frictionless particles[J]. Physical Review Letters, 2002, 88(7): 1-4.
[17]BENABBOU A, BOROUCHAKI H, LAUG P, et al.Numerical modeling of nanostructured materials[J].Finite Elements in Analysis and Design, 2010, 46(1-2):165-180.

