三维应力状态下砂的临界状态本构模型分叉分析

甄文战，孙德安，陈瑶瑶

（上海大学 土木工程系，上海 200072）

1 引 言

在三轴剪切试验中，常观察到密砂试样整体承载能力在达到一个峰值荷载水平之后，随着变形的增加而承载力降低。即：岩土材料在应力达到强度极限后，随变形的继续增加，其强度值将迅速降低到一个较低的水平，这种由变形引起的材料性能劣化的现象称为应变软化现象。

岩土材料从硬化到软化阶段的转变一般认为是材料变形模式分叉造成的。对于服从关联流动法则的岩土材料，在材料峰值强度前材料一般是稳定的，在峰值点处，材料切向刚度矩阵奇异，材料失稳，变形模式开始出现分叉，通常认为峰值点即为分叉失稳点，从而分叉后引起应力-应变关系不再具有惟一性。但对于服从非关联流动法则的岩土材料，由于材料的刚度矩阵不对称，则分叉点有可能出现应力-应变关系的硬化阶段。

分叉理论为研究服从非关联流动法则的软化材料失稳提供了理论基础。在分叉理论研究方面，Hill[1－2]最早用分叉理论建立了预测应变局部化的理论框架。Rudnicki和Rice[3]，Rice[4]在Hill理论框架下继续深入研究，并在此基础上提出应变局部化判别准则的具体表达试，并成为了目前应变局部化研究的主要理论基础。此后，许多学者[5－6]仍致力于分叉理论的研究，但主要集中对平面应变二维问题的分析，而对不同应力路径下分叉的三维特性研究还非常少。

本文基于姚仰平等[7]提出可以考虑平均应力水平及孔隙比影响的砂临界状态三维弹塑性本构模型，就服从非关联流动法则的软化型本构模型在不同加载路径下进行了分叉理论分析。讨论了不同应力路径下分叉特性，给出了分叉点对应的应力比、主应变及剪切带倾角随应力洛德角变化的趋势。最后，编写本构模型材料子程序，实现了该模型与有限元 ABAQUS软件的结合，通过对立方体密砂试样的数值模拟，证明了分叉现象的存在，并捕捉到了分叉点的应力状态，验证了理论解的正确性。

2 临界状态本构模型

砂的变形特性受平均应力水平及孔隙比的影响。初始状态很松的砂呈硬化型应力-应变关系，而中密砂受剪时呈现先硬化后软化的应力-应变关系。为了反映砂的上述变形特性，Yao等[7]提出了一个砂的临界状态本构模型，该模型不仅可以反映松砂强度低、体缩大的变形特性，还可以反映中密砂及密砂的剪胀、应力-应变关系软化的变形特性。该模型认为，存在一条临界状态线(CSL)，斜率为λ，如图 1所示。参考线(RCL)平行于临界状态线，该线以上的点 A表示松砂状态。砂在最密时的状态线(DCL)对应于加荷再卸荷曲线，斜率为κ。砂的临界状态本构模型采用 SMP准则，通过变换应力[8]的方法实现了该模型三维化。该方法假定在三轴压缩条件下变换应力与原应力相同，使得在原应力空间下π平面上为曲边三角形的SMP准则，在变换应力空间的π平面上为圆形，变换应力σ~ij公式为

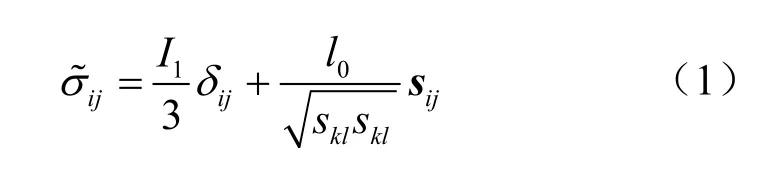
其中，

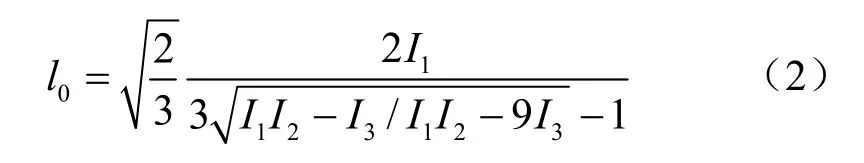
式中： δij为克罗内克尔参数；sij为偏应力张量；I1、I2、I3分别为第1、2及第3应力不变量。

该模型屈服函数f及塑性势函数g表达式为[7]

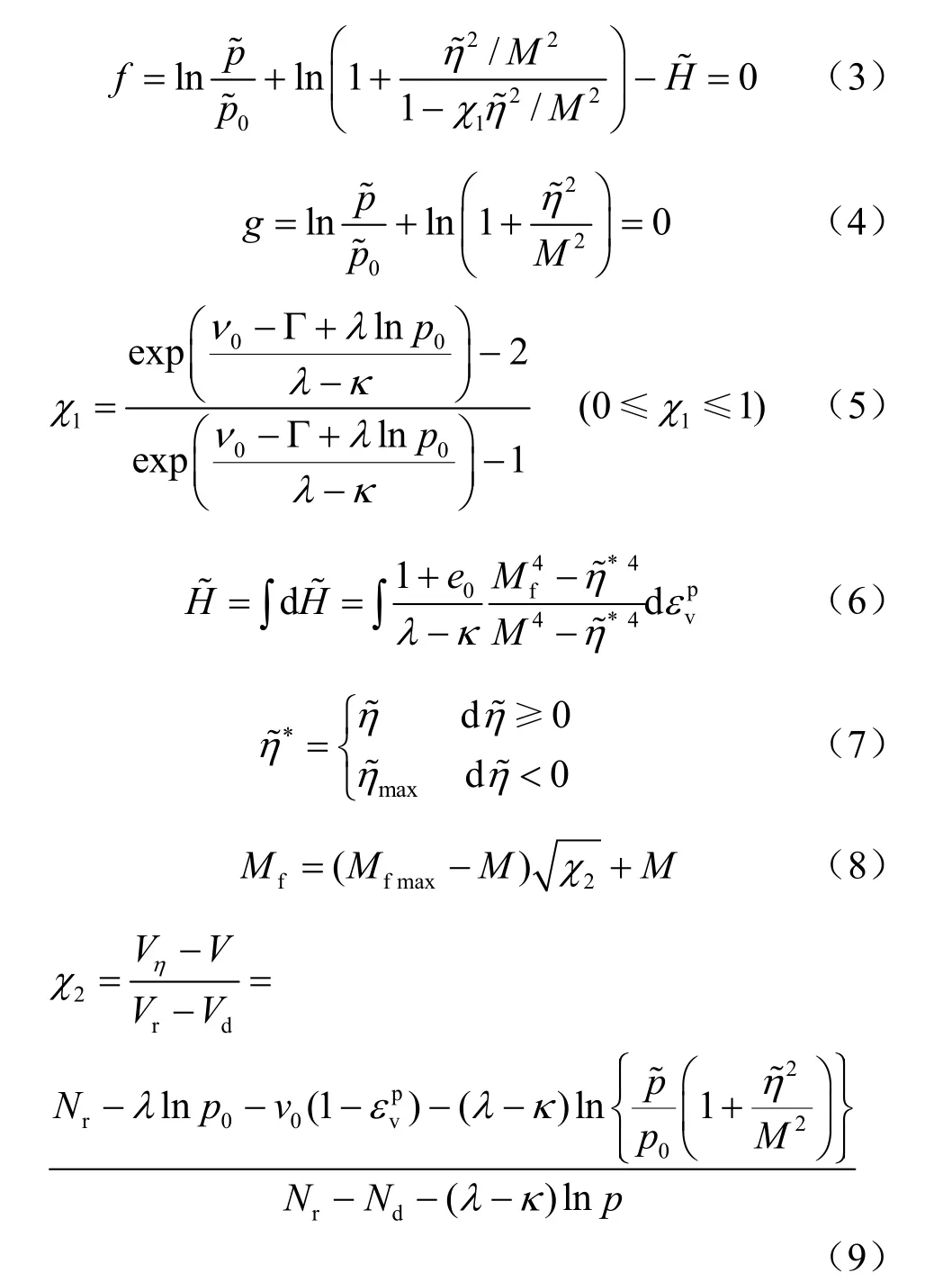
式中：上标～表示为变换应力空间中的值； λ为压缩指数；κ为回弹指数；e0为初始孔隙比；为塑性体积应变；分别为初始平均应力、平均应力；为应力比；比容 v0= 1+e0；Mfmax、M分别为最大及临界状态时的应力比； H~为硬化参数；为当p =1 kPa时参考线、临界状态线及最密状态线的比容；为p时参考线、应力比η~、临界状态线及最密状态线的比容。

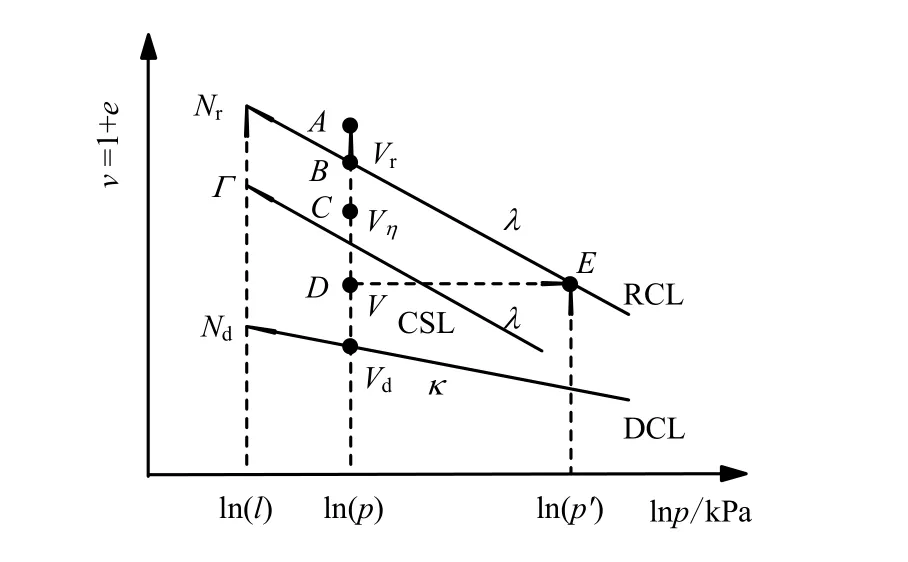
图1 比容－平均应力平面中砂的密实状态表示[7]Fig.1 Sand with different initial densities in v-lnp plane[7]

3 分叉理论分析

理论研究认为：应变软化并不是发生分叉现象的惟一原因。Rudnicki和Rice证明了在采用非关联流动法则的情况下，即使在应变硬化时仍可能发生分叉现象[3]。而服从非关联流动法则的软化模型在不同应力路径下的分叉特性如何？下面就此问题进行理论分析。

3.1 分叉理论

Rice等[4]认为，速度场在剪切带内保持连续，而速度梯度通过剪切带产生跳跃，但速度和速度梯度在平行于局部化变形带方向仍保持均匀，而变形场在带外保持均匀。如图2所示，在S面上速度场保持连续，而速度梯度场产生跳跃。在这一假设条件下提出了经典的分叉判别准则：

图2 三维应力状态下剪切带示意图Fig.2 Shear band under 3D stress state

3.2 分叉判别式

根据岩土材料的真三轴试验现象[9]，假定剪切带的法线方向垂直于中主应力方向，即剪切带沿中主应力方向不发生变化，但中主应力的大小影响分叉的产生条件。将n2=0代入行列式(10)中，即得：

砂的临界状态本构模型本构张量表达式为

其中：

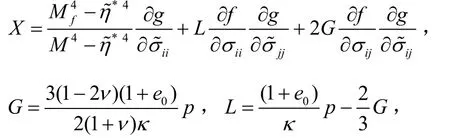
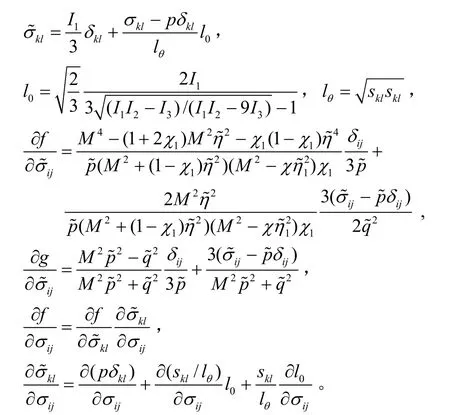
式中：ν为泊松比。因屈服函数与塑性势函数不同，即f≠g，所以该本构模型为非关联模型。

方程(11)有实数解，出现局部化分叉判别式为

3.3 三维应力状态的分叉条件

在等平均应力(p=200 kPa)下，不同应力洛德角下的条件为

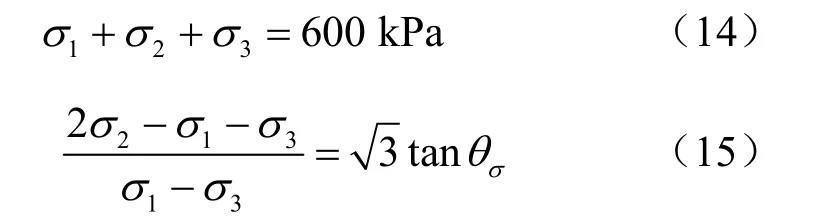
当θσ为25o、±15o、0o及±30o时，联立式(13)～(15)，可求得在等p下初始孔隙比为0.68时，不同应力洛德角（如图3所示）对应的局分叉理论解。模型材料参数取自文献[7]，见表1。

3.4 三维应力状态下分叉结果

表2为不同应力路径下分叉理论解，并给出了分叉时对应的应力比、主应变及剪切带倾角值。

图3 π平面上应力洛德角Fig.3 Lode’s angle in π-plane

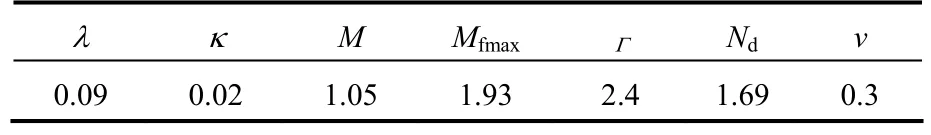
表1 砂的模型参数Table 1 Model parameters for sand

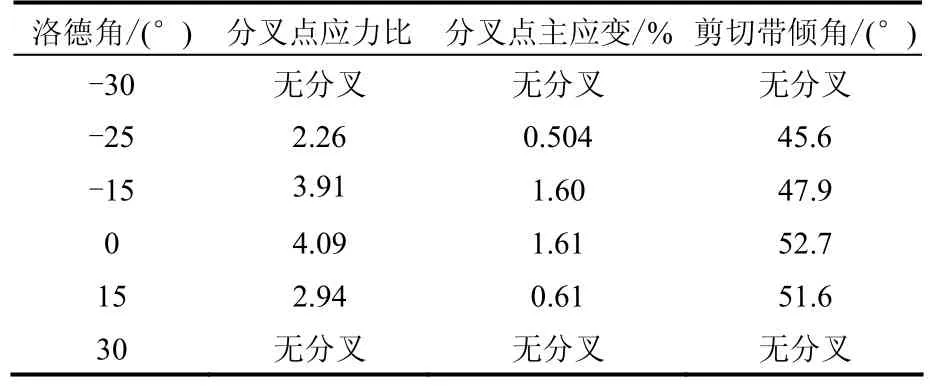
表2 分叉理论解Table 2 Theoretical solutions to bifurcation

图4表示了分叉时(不分叉区域的上围包线)对应的应力比或主应变随应力洛德角的变化趋势。由图可知，分叉受应力路径的影响，即随着应力洛德角的变化表现出不同的分叉特性。罗德角在-25°～15°之间变化时均能产生分叉，且该分叉解随洛德角变化规律与文献[10]试验结果基本一致。并且分叉时对应的应力比或主应变均随洛德角的增加先增加而后减小。图4还分别给出了不同洛德角时不分叉区域范围。即当洛德角和对应的应力比或主应变在不分叉区域内就不会出现分叉现象。根据该图可以对是否出现分叉进行判别。

图4 不同应力路径下不分叉区域Fig.4 Ranges of no bifurcation at different stress paths

图5为剪切带倾角随洛德角变化情况，由图可知，随着洛德角的增加(-25°～0°)，剪切带倾角增长较大，而后稍微减小，且分叉时剪切带倾角(对应剪切带出现最早时刻值)均大于45°。

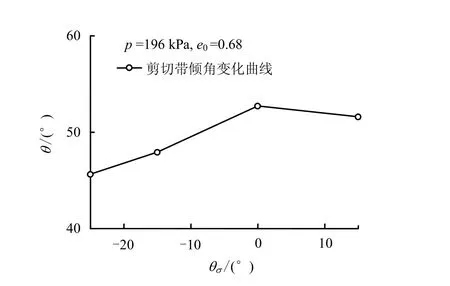
图5 不同应力路径下剪切带倾角变化曲线Fig.5 Relationship between inclination angle of shear band and Lode’s angle

3.5 孔隙比对分叉结果的影响

通过以上分析可认为：是否出现局部化分叉受应力路径的影响。但同一应力路径下的分叉结果又受孔隙比的影响，即孔隙比的大小影响着分叉点在应力-应变关系上出现的位置。为了分析孔隙比对分叉的影响，在平面应变-应力路径下分析不同孔隙比下的分叉和峰值应力比。图6表示了围压一定时的计算结果。由图可知，分叉点对应的应力比(分叉应力比)随孔隙比的增加而减小，但分叉点对应的分叉应力比小于峰值应力比，则说明分叉出现在应力-应变关系硬化阶段。

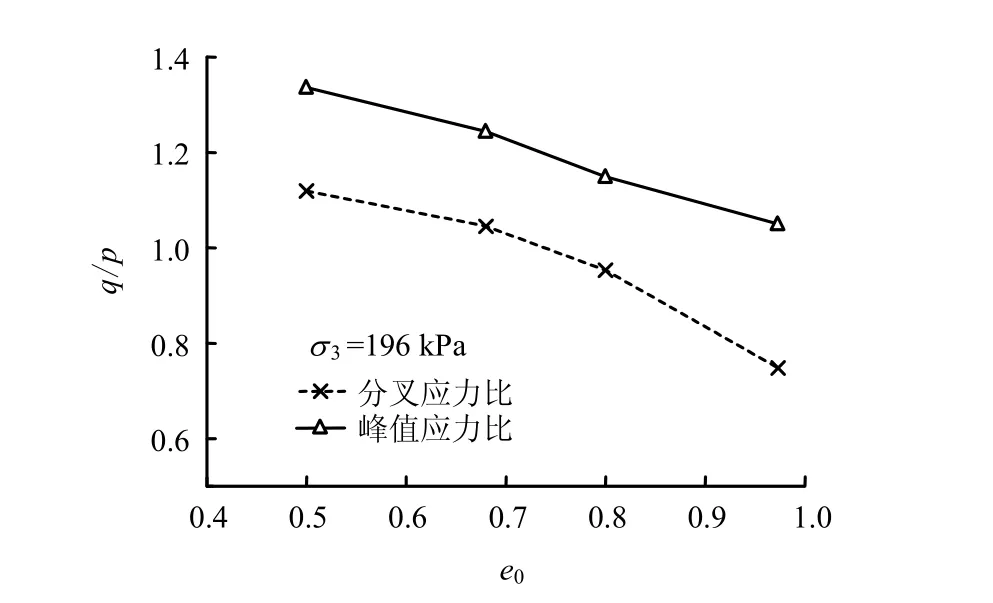
图6 应力比随初始孔隙比变化曲线Fig.6 Relationships between stress ratio and initial void ratio

4 真三轴数值模拟

经典本构关系理论建立在连续介质力学基础之上，虽具有严密的数学理论框架，但却难以描述应变局部化问题，在有限元分析中存在很大的局限性。在接近破坏条件出现失稳分叉时，高应变区呈现局部化，且该区域内许多单元积分点处的声张量成为奇异(刚度矩阵失去正定性，特征值出现负值)，拟静力问题的偏微分控制方程丧失椭圆型，这使得所考虑的边值问题变为病态，其解出现非适定性[11]。

为了在不同应力路径下通过数值方法预测分叉现象，作者在在文献[12－13]的基础上，采用半隐式回映应力更新算法，编写了临界状态本构模型的子程序，程序流程图如图7所示。把该模型嵌入到有限元程序 ABAQUS中，从而实现了在数值计算中得以捕捉分叉(刚度矩阵出现负特征值)时对应的应力状态的方法。

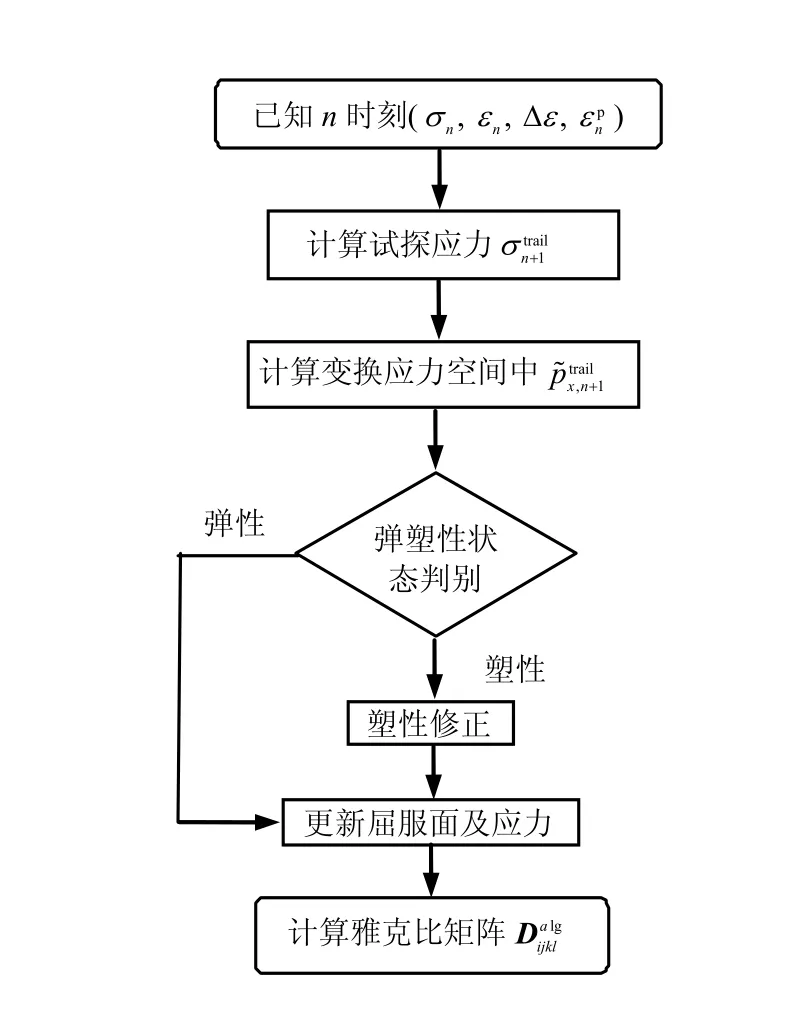
图7 子程序流程图Fig.7 Flow chart of the subroutine

4.1 子程序单元测试

为了验证子程序的精度，取一个单元进行子程序特性测试。并与丰浦砂的三轴压缩试验结果进行了比较，如图8所示，初始孔隙比e0=0.68时的应力-应变的计算曲线与试验结果基本一致，验证了程序的正确性。

4.2 数值分析方案

为了通过数值方法对本构模型在不同应力路径的分叉特性进行预测，取一个各向同性均匀的立方体，边长为10 cm。将试样划分为14×14×14=2 744个单元，有限元网格划分如图9所示，其中1方向为大主应力方向。为了在ABAQUS中实现等p时不同应力路径下的数值模拟，采用多步试算的方法确定围压变化幅值曲线，通过围压设定荷载幅值曲线的方法，成功实现了等p时不同应力路径下的数值预测。数值预测采用的模型参数同上表1。

图8 主应力比-应变关系Fig.8 Relationships between stress ratio and strain

图9 有限元网格Fig.9 Meshes for finite element analysis

4.3 数值预测结果与理论解比较

图10给出了不同应力路径下数值预测分叉点对应的应力-应变状态。数值计算时取负特征值(negative eigenvalue)出现对应的应力状态为分叉点。其原因是从 ABAQUS计算方法上分析，负特征值表示在应力-应变关系曲线的硬化阶段出现负斜率，与原应力-应变关系不同，控制偏微分方程由椭圆型转化为双曲线型，即分叉；从数学上分析，出现负特征值，刚度矩阵不正定，方程组存在多组解，从而可判定数值计算的分叉点。

由图可知，理论上只要在该应力路径下存在分叉点时，通过数值方法也同样捕捉到了分叉点的状态，证明了分叉现象在数值计算中的存在。同时，通过图中理论解及数值预测分叉点的对比，可以发现数值预测结果也与理论解基本一致(应力比最大误差为θσ=0°对应的值11.4%)。

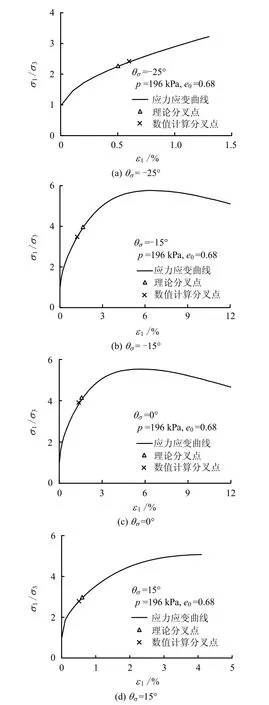
图10 分叉点的理论和数值预测Fig.10 Theoretical and numerical predictions of bifurcation

5 结 论

（1）理论分析表明：分叉现象强烈依赖于应力路径，即应力洛德角在-25°～15°之间变化时，均会在应力-应变关系硬化阶段出现分叉现象，而其他应力路径下不会产生分叉。但同一应力路径下的分叉结果受孔隙比的影响。且分叉时对应的应力比、主应变及剪切带倾角都随洛德角而变化，其值均先增加而后减小。

（2）通过数值方法预测到了分叉点对应的应力状态，数值预测值和理论解的结果基本一致。

[1]Hill R. A general theory of uniqueness and stability in elastic-plastic solids[J]. Journal of the Mechanics and Physics of Solids, 1958, 5: 236－249.

[2]HILL R A, HUTCHINSON J W. Bifurcation phenomena in the plane tension test[J]. Journal of the Mechanics and Physics of Solids, 1975, 23: 239－264.

[3]RUDNICKI J W, RICE J R. Conditions for the localization of deformation in pressure-sensitive dilatant materials[J]. Journal of the Mechanics and Physics of Solids, 1975, 23: 371－394.

[4]RICE J R. The localization of plastic deformation[C]//Proceedings of 14th International Conference on Theoretical and Applied Mechanics. [S. l.]: [s. n.], 1976:207－220.

[5]VARDOULAKIS I, GOLDSCHEIDER M, GUDEHUS G.Formation of shear bands in sand bodies as a bifurcation problem[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1978, 2(2): 99－128.

[6]OTTOSEN N S, RUNESSON K. Properties of discontinuous bifurcation solutions in elasto-plasticity[J].International Journal of Solids and Structures, 1991,27: 231－254.

[7]YAO Y P, SUN D A, LUO T. A critical state model for sands dependent on stress and density[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2004, 28(4): 323－337.

[8]MATSUOKA H, YAO Y P, SUN D A. The Cam-clay model revised by the SMP criterion[J]. Soils and Foundations, 1999, 39(1): 81－95.

[9]松冈元, 中井照夫. Closure to discussion on “Stressdeformation and strength characteristics of soil under three-different principal stress[M]. 日本: [s. n.], 1976.

[10]WANG Q, LADE P V. Shear banding in true triaxial tests and its effect on failure in sand[J]. Journal of Engineering Mechanics, ASCE, 2001, 127(8): 754－761.

[11]BAZANT Z P, BELYTSCHKO T, CHANG T P.Continuum theory for strain softening[J]. Journal of Engineering Mechanics, ASCE, 1984, 110: 1666－1692.

[12]孙德安, 甄文战, 黄文雄. 三维弹塑性模型在路堤软基固结分析中应用[J]. 岩土力学, 2009, 30(3): 669－674.SUN De-an, ZHEN Wen-zhan, HUANG Wen-xiong.Application of 3D elastoplastic model to analysis of consolidation behavior of embankment on soft soils[J].Rock and Soil Mechanics, 2009, 30(3): 669－674.

[13]孙德安, 甄文战. 不同应力路径下剪切带的数值模拟[J]. 岩土力学, 2010, 31(7): 2253－2258.SUN De-an, ZHEN Wen-zhan. Numerical simulations of shear bands along different stress paths[J]. Rock and Soil Mechanics, 2010, 31(7): 2253－2258.