深部洞室围岩分区破裂化的冲击破坏机制研究

陈建功 ，周陶陶 ，张永兴

（1. 重庆大学 土木工程学院，重庆 400045；2. 重庆大学 山地城镇建设与新技术教育部重点实验室，重庆 400045）

1 引 言

分区破裂化是指在深部岩体工程中开挖洞室或坑道时，会在围岩中产生交替的破裂区和非破裂区的现象[1]。20世纪70年代 Adams和Jager在南非Witwatersrand金矿2 000～3 000 m深处采场采用钻孔潜望镜观测到顶板间隔破裂现象，并排除了分区破裂化现象的产生是由于爆破引起的，即不论是在钻爆法施工的巷道还是采用机械化施工的巷道中，只要条件满足，巷道围岩都会产生此现象[2－3]。俄罗斯科学院(原苏联科学院)西伯利亚分院Shemyakin等于20世纪80～90年代对分区破裂化现象进行了深部矿井现场试验研究、实验室模拟研究、理论分析以及现象的应用研究[4－7]。Курленя和 Опарин[8]在对大量试验数据的分析和理论研究基础上，发现各破裂区的半径服从某种规律，给出了各破裂区的半径和厚度表达公式，但该公式仅适用于特定矿区。近年来，随着深部工程的不断增加，深部一些新的岩石力学现象不断出现，中国的学者开始关注并开展了深部围岩特性的研究[9]。在淮南矿区的深部矿井巷道围岩钻孔中用钻孔窥测仪观察到了分区破裂化效应的存在[10]；通过实验室模拟试验也获得了分区破裂化现象[11－12]；通过数值计算再现了均匀介质岩体中的巷道围岩分区破裂化现象[13－14]。在这些研究中，有的仅考虑了基于莫尔–库仑强度理论的剪切滑移破坏，并未得到明显的分区破裂化效应。

钱七虎院士在国内率先介绍了国外学者关于分区破裂化现象研究的成果，研究了深部岩体工程响应的特征，并且界定了“深部”岩体的范围[15]，提出深部围岩分区破裂化现象是一个与空间、时间效应密切相关的科学现象，用传统的连续介质弹塑性力学不能完全解释清楚。认为分区破裂化效应的产生，一方面是由于高地应力和开挖卸荷导致围岩的“劈裂”效应；另一方面是由于围岩深部高地应力和开挖面应力释放所形成的应力梯度而产生的能量流。Shemyakin认为，深部巷道围岩在卸荷条件下裂缝的产生，是在应力集中导致的最大支撑压力作用处，由于巷道自由面的影响，产生径向拉伸变形并达到围岩的极限应变，导致第1个破坏区中裂缝的张开，以及围岩向着巷道自由面位移的发展导致了“伪掌子面”，即“伪自由表面”的形成，从而引起围岩再次发生应力重分布。应力重分布将导致第2个“伪自由表面”的形成，从而进一步引起围岩内应力的重分布。上述过程不断发展，一直延续到围岩重分布的应力达不到围岩的破坏条件为止。这种对分区破裂化机制的解释仅仅是定性的。本文试图从应力波波前不连续间断面角度来探讨分区破裂化的形成机制，进而定量确定围岩中各个破坏区厚度以及半径关系。

2 分区破裂化的冲击破坏机制

在高地应力下岩体受到扰动时，其力学性能首先表现为弹性和脆性，然后随着变形的发展才表现为黏塑性。所以在开挖瞬间，围岩应力重分布由围岩的弹性性质决定，首先在围岩压力的静力作用下产生应力重分布，然后因开挖扰动产生的径向应力波（P波）向围岩内部传递，此波波前就是一个压力间断面，其两侧分别是此间断面位置的静力解和动力解，因动力解随时间收敛于静力解，且其值始终小于静力解，当此间断面处的压力降满足冲击波产生的条件时就产生冲击破坏，在波前径向压力降峰值处附近形成一环状破裂带，如图1所示。这也是为什么破坏区岩石很粉碎，不同于其他破坏形式的原因。由于冲击波以超声速传播，其冲击破坏在瞬间完成，相当于在原来的介质内又形成了一个新的开挖界面，又会重复出现这样的冲击破坏区，这种冲击破坏一直进行到围岩内由所产生的波前径向压力降不满足冲击条件时为止。上述断续的冲击破坏过程使洞周围岩内产生交替的破坏及未破坏区域，即分区破裂化现象。

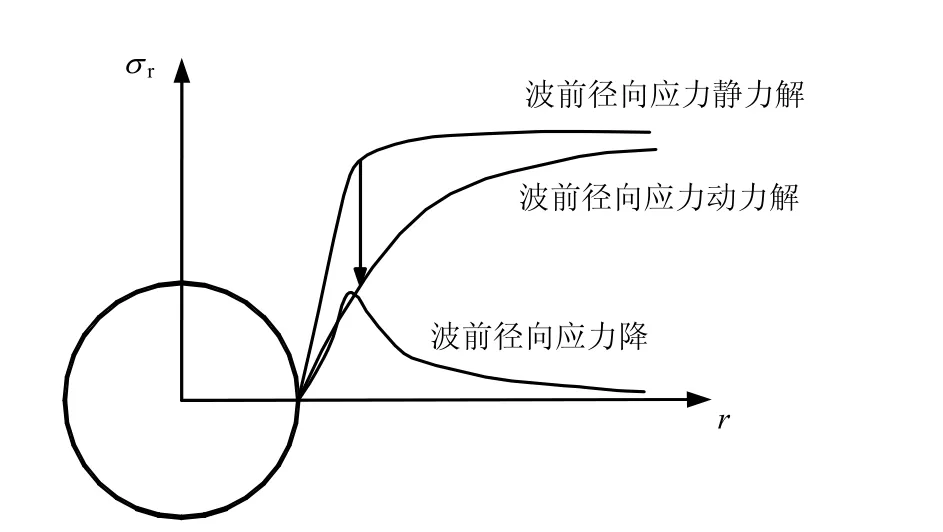
图1 波前径向应力分布Fig.1 Distribution of radial stress at wave front

3 球形洞室开挖的径向应力分析

对于无限介质中一半径为r0的球形洞室，假设岩体处于静水压力p0状态，其开挖问题可分为两个分问题的叠加，一是在无穷远处作用有原岩应力p0，在洞室内壁上作用有一个均布压力p0，即由原岩应力所引起的应力和位移；二是无原岩应力的作用，在开挖瞬间t=0时刻，在洞室内壁上突然作用一均布拉力p(t)所产生的应力和应变。两者之和为开挖瞬间围岩介质的应力场和位移场，见图 2。第1个问题比较容易解答，问题2归结为在球形腔内壁上突然作用一均布拉力p(t)所引起的瞬态动力学问题。

问题1的弹性力学解：

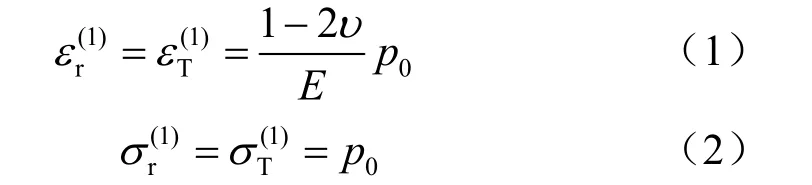
问题2归结为在洞室内壁上突然作用一均布拉力p(t)所引起的瞬态动力学问题。

式中：H(t)为Heaviside单位阶跃函数，满足：

图2 球形巷道开挖过程的力学模型分解Fig.2 Two parts from mechanical model of spheric tunnel during excavation process

在球对称拉力p(t)的作用下围岩介质产生具有球对称性的无旋波，而不会产生弥散波，也就是只有p波，不产生s波，设位移函数为φ，应满足波动方程：

式中：cd为纵波波速，为拉梅常数，ρ为介质密度；t为时间变量，在球对称坐标系（r,θ,ϕ）下，上式可简化为

问题相应的边界及初始条件如下：

由弹性动力学理论，上述问题的位移势解为

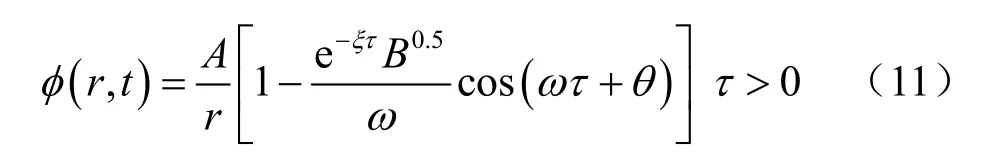
径向位移为

由弹性理论，应力张量在球坐标中的分量为

将式（6）、（12）代入式（13）得：

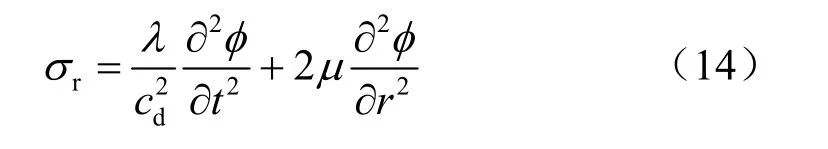
将式（11）代入式（14）得到问题2的径向应力为

这样可以得到在空间球对称下球形洞室开挖的围岩动态径向应力场为

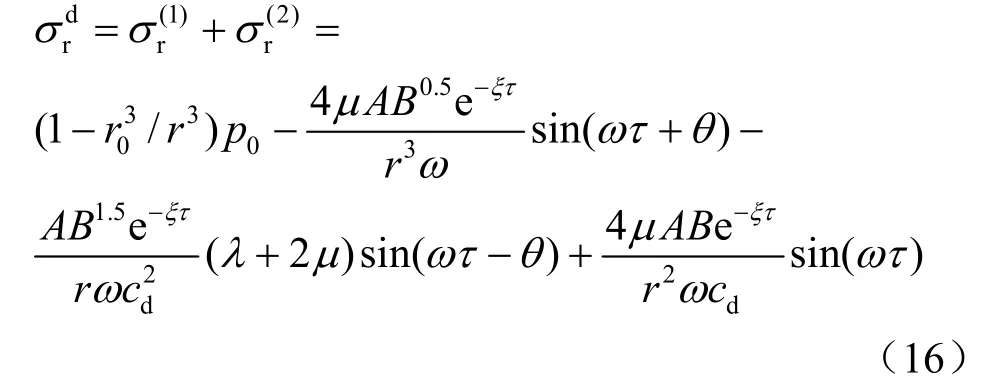
把τ=0代入式（16），得到波前应力为

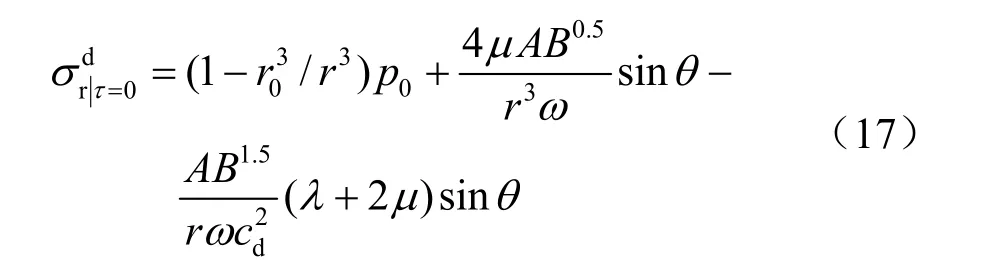
无限大空心球腔内侧压力为 0，外侧受均布压力p0作用下的静态径向压力场为

波前应力降：

由上一节分析可知，在波前径向应力降峰值附近会冲击破坏，破裂区中心半径位于波前径向应力降峰值处，由得：

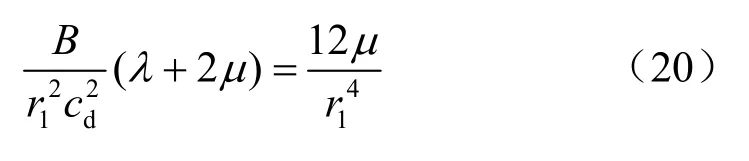
在第1个破裂区产生之前，未扰动围岩内的静态径向应力为：

第1个破裂区产生后，形成新的伪开挖面时，由于是冲击压缩破坏，冲击波向开挖面方向传播，故忽略破裂区围岩的残余支撑压力。此伪开挖面处的卸荷压力Δp可由下式得到：

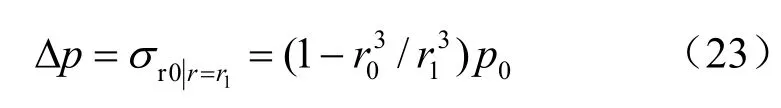
要分析此时的动态径向应力场，同样可分成两个子问题。问题1为第1个破裂区产生之前未扰动围岩内的静态径向应力；问题2为在球形腔内壁上突然作用一均布拉力Δp所引起的动态径向应力场由式（15）可得：

动态径向应力场为

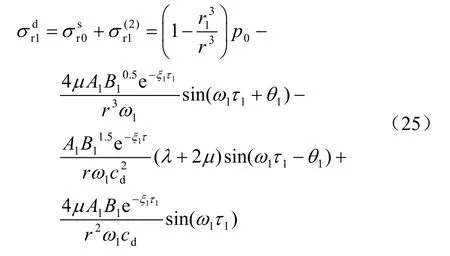
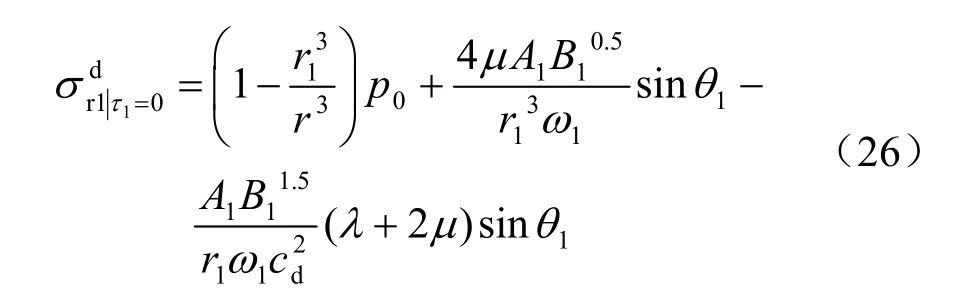
当第1个破裂区产生瞬间，未扰动围岩内的静态径向应力又得到重分布，由下式表示：

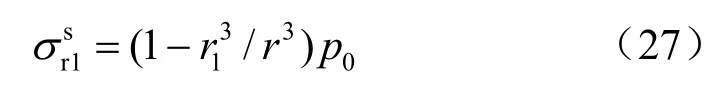
波前应力降为

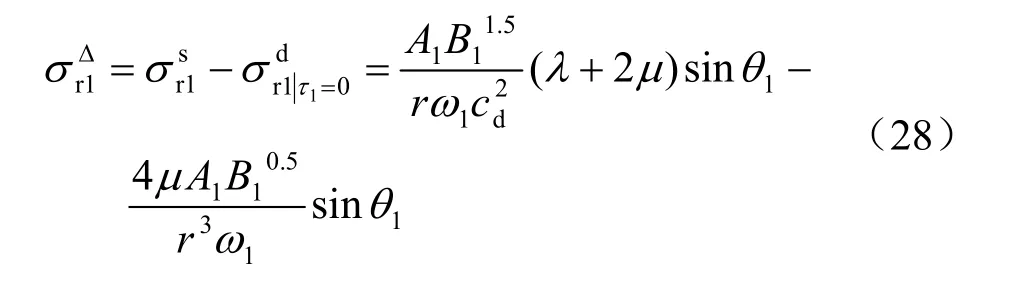
同样在波前径向应力降峰值附近会冲击破坏，破裂区中心半径r2位于波前径向应力降峰值处，由得：

由于式（19）和式（28）具有相同的形式，可以得出以下结论：

①发生各次分区破裂化时，波前径向应力降可以用下面的统一公式计算：

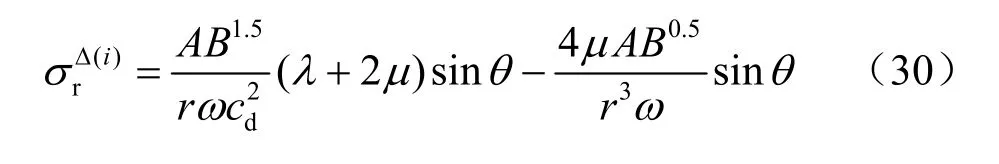
②破裂区半径只取决于开挖面半径，同样，第1个破裂区产生后形成新的伪开挖面时，所产生的第2个破裂区半径也只取决于第1个破裂区半径，其比值也为可见球形洞室开挖产生分区破裂化时，巷道半径及各破裂分区半径成等比数列，等比值为即：

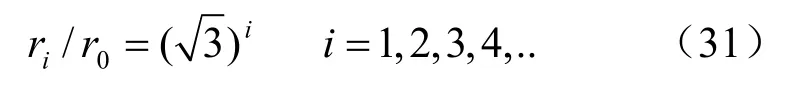
式中：i为破裂区的编号。

比较接近，等比值的不同主要源于本文所采用的球形洞室作为分析模型，而文献[15]是针对圆形巷道而言。

4 围岩分区破裂化的冲击本构方程和破坏准则

早在20世纪60年代，著名岩石力学专家耶格和库克在他们的经典著作《岩石力学基础》中提出，应力或应变并不一定是结构破坏的位移原因，Duvall等曾总结了许多研究者的工作，认为质点的振动速度也会使结构产生破坏的原因，其结论是如果质点速度达到0.2m/s时就会发生大的结构破坏，如果质点速度小于0.025 s，则无破坏。根据本文提出的冲击破坏机制，冲击破坏的本构模型应结合质点速度、间断压力降，由动量守恒定律给出，破坏准则取决于质点速度的限定值。

4.1 冲击本构方程

波阵面的运动是波动传播的一种极限形式，在波阵面两侧的运动是不连续的。波阵面前方的质点处于静止状态，波阵面后方的质点处于运动状态，其两侧的一些物理量必定是不连续的，因而波阵面是间断面。在一级间断面上，物质的变形梯度和速度是不连续的间断面即为冲击波，间断面上除满足几何相容和运动相容条件外，还必须满足动力相容条件。这里引入动力守恒方程：

式中：a、b为岩石常数，可通过试验确定，将上式代入式（32）得：

上式即为冲击荷载下的本构方程。

4.2 冲击破坏准则

由式（34）可以根据波前压力降得到冲击波作用下岩石质点振动速度，当此振速超过某一数值时，即产生冲击破坏。设一沿x方向以波速为D传播的冲击波且函数：

代表此方向的波长为L、振幅为F0的简谐波，若F为位移，则此波的质点速度为

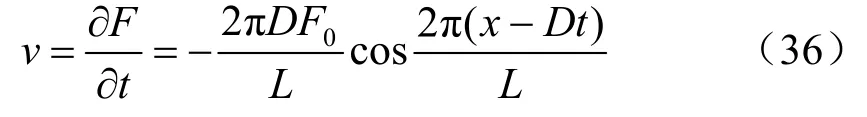
由此引起的应变为

比较式（36）、（37），质点的速度和应变有以下关系：

将式（33）代入式（38）得：

因为冲击破坏表现为岩石的瞬间压缩破坏，采用最大压应变强度准则：

式中：εcr为岩石单轴抗压强度相对应的极限压应变。

冲击荷载下的本构方程式（34）也可表示为

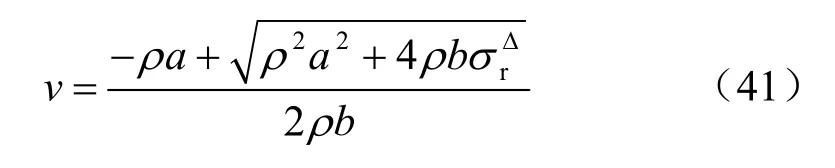
忽略压应力的负号，由式（39）、（40）、（41）得：

为产生冲击破坏的临界压力降，式（42）即为岩石冲击破坏准则。

5 算例分析

设球形洞室的半径为 r0= 2.5 m，围岩主要为砂质泥岩，原岩应力为p0=35 MPa，弹性模量E=5.25 GPa，密度ρ=2.57 g/cm3，泊松比 υ= 0.276，极限压应变εcr=1.5×10-3，砂质泥岩岩石常数a= 1 850 m/s 、b=1.60。根据式（16）计算结果得出，图3动态径向应力场，图中径向拉应力为正，从图中可以看出，在洞周附近，径向拉应力急剧下降，远离洞周时，波前应力衰减速度比较平缓。图4为波前径向应力动、静力曲线和波前压力降曲线。由图可知，波前动应力随半径的衰减速度比静应力要快，这样导致在波前产生压力降，此压力降在某一位置有一峰值导致冲击破坏。

图3 球形洞室开挖过程的围岩径向应力扰动场Fig.3 Disturbed field of radial stress in surround rock during excavation process

波前压力降曲线与临界压力降线相交于两点，分别为内、外边界点，两点之间的区域即为第1破裂区。计算得内边界点半径r1i=3.90 m、r1o=4.85 m。

通过计算可以得到另外两个破裂区的范围，具体见表1。

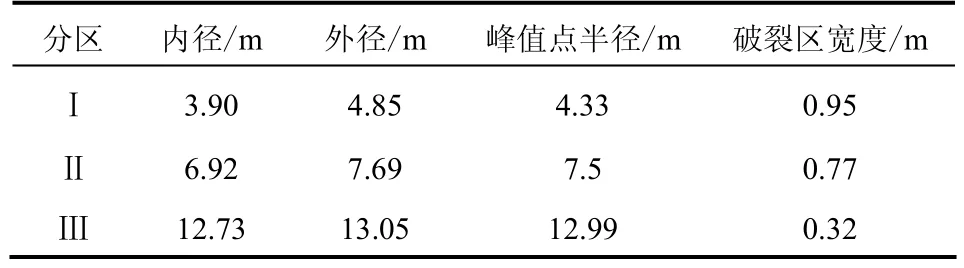
表1 破裂区宽度Table 1 The widths of fractured zones

6 结 论

深部洞室围岩分区破裂化现象是由于岩体开挖引起的围岩应力重分布过程中，径向应力产生了间断面，当此间断面压力差满足产生冲击波条件时，即产生冲击破坏，当此冲击波衰减很快，其传播距离无法达到围岩内壁时，所产生的是局部分区破裂，而不会产生岩爆。当间断面的条件达不到产生冲击条件时，围岩受力变形状态就属于浅部围岩的情况。

（1）推导了洞室开挖瞬间围岩径向应力场的动力学理论解，得到了发生各次分区破裂化时，波前径向应力降的统一计算公式。

（2）根据质点速度、间断面压力降，由动量守恒定律推导了围岩分区破裂化的冲击本构方程和破坏准则，得到了产生冲击破坏的间断面压力降临界值计算公式。

（3）在球形洞室及等应力条件下，当产生分区破裂化现象时，各破裂区半径只取决于开挖面（或伪开挖面）的半径，且成等比数列，等比值为 3。

[1]钱七虎. 非线性岩石力学的新进展—深部岩体力学的若干问题[C]//中国岩石力学与工程学会编.第八次全国岩石力学与工程学术大会论文集. 北京: 科学出版社,2004: 10－17.

[2]CLOETE D R, JAGER A J. The nature of the fracture zone in gold mines as revealed by diamond core drilling[R]. [S. l.]: Association of Mine Managers, 1972.

[3]ADAMS G R, JAGER A J. Petroscopic observations of rock fracturing ahead of stope faces in deep-level gold mine[J]. Journal of the South African Institute of Mining and Metallurgy, 1980, 80(6): 204－209.

[4]SHEMYAKIN I, FISENKO G L, KURLENYA M V, et al.Zonal disintegration of rocks around underground workings I. Data of in-situ observations[J]. Soviet Mining Science, 1986, 22(3): 157－168.

[5]SHEMYAKIN I, FISENKO G L, KURLENYA M V, et al.Zonal disintegration of rocks around underground workings II. Disintegration of rocks on models of equivalent materials[J]. Soviet Mining Science, 1986,22(4): 223－232.

[6]SHEMYAKIN E I, FISENKO G L, KURLENYA M V,et al. Zonal disintegration of rocks around underground workings III. Theoretical notions[J]. Soviet Mining Science, 1987, 23(1): 1－6.

[7]SHEMYAKIN E I, FISENKO G L, KURLENYA M V,et al. Zonal disintegration of rocks around underground workings IV. Practical applications[J]. Soviet Mining Science, 1988, 24(3): 297－302.

[8]КУРЛЕНЯ М В, ОПАРИНВН. Проблемы нелинейной геомеханики Ч.1[J]. ФТПРПИ, 1999, (3): 12－23.

[9]李德忠, 李冰冰, 檀远远. 矿井深部巷道围岩变形浅析及控制[J]. 岩土力学, 2009, 30(1): 109－112.LI De-zhong, LI Bing-bing, TAN Yuan-yuan. Analysis and control of distortion of surrounding rock of roadway at deep ground of mine[J]. Rock and Soil Mechanics,2009, 30(1): 109－112.

[10]李术才, 王汉鹏, 钱七虎, 等. 深部巷道围岩分区破裂化现象现场监测研究[J]. 岩石力学与工程学报, 2008,27(8): 1545－1553.LI Shu-cai, WANG Han-peng, QIAN Qi-hu, et al. In-situ monitoring research on zonal disintegration of surrounding rock mass in deep mine roadways[J].Chinese Journal of Rock Mechanics and Engineering,2008, 27(8): 1545－1553.

[11]顾金才, 顾雷雨, 陈安敏. 深部开挖洞室围岩分层断裂破坏机制模型试验与分析[J]. 岩石力学与工程学报,2008, 27(3): 433－438.GU Jin-cai, GU Lei-yu, CHEN An-min. Model test study on mechanism of layered fracture within surrounding rock of tunnels in deep stratum[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(3): 433－438.

[12]陈旭光, 张强勇. 高应力深部洞室模型试验分区破裂现象机制的初步研究. [J]. 岩土力学, 2011, 32(1): 84－90.CHEN Xu-guang, ZHANG Qiang-yong. Mechanism analysis of phenomenon of zonal disintegration in deep tunnel model test under high geostress[J]. Rock and Soil Mechanics, 2011, 32(1): 84－90.

[13]周小平, 钱七虎. 深埋巷道分区破裂化机制[J]. 岩石力学与工程学报, 2007, 26(5): 877－885.ZHOU Xiao-ping, QIAN Qi-hu. Zonal fracturing mechanism in deep tunnel[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(5): 877－885.

[14]唐春安, 张永彬. 岩体间隔破裂机制及演化规律初探[J]. 岩石力学与工程学报, 2008, 27(7): 1362－1369.TANG Chun-an, ZHANG Yong-bin. Discussion on mechanism and evolution laws of fracture in rock mass[J].Chinese Journal of Rock Mechanics and Engineering,2008, 27(7): 1362－1369.

[15]钱七虎. 深部岩体工程响应的特征科学现象及“深部”的界定[J]. 华东理工学院学报, 2004, 27(1): 1－5.QIAN Qi-hu. The characteristic scientific phenomena of engineering response to deep rock mass and the implication of deepness[J]. Journal of East China Institute of Technology, 2004, 27(1): 1－5.

[16]戴俊. 岩石动力学特性与爆破理论[M]. 北京: 冶金工业出版社, 2002.