基于鱼雷壳体强度及稳定性的结构可靠性分析
郭 君1, 蒋忠亮2, 秦晓辉1, 刘 津1
基于鱼雷壳体强度及稳定性的结构可靠性分析
郭 君, 蒋忠亮, 秦晓辉, 刘 津
(1. 中国船舶重工集团公司第705研究所, 陕西西安, 710075; 2. 西安近代化学研究所, 陕西西安, 710065)
针对现有结构设计安全系数方法的弊端, 将可靠性设计理念引入鱼雷结构设计领域。结合经典壳体理论计算方法与二次二阶矩法, 确定了基于理论公式的壳体结构可靠性安全裕度方程及其求解方法, 利用ANSYS软件的概率设计(PDS)模块从有限元角度对壳体结构可靠性进行计算, 计算结果验证了该方法的准确性。以上2种方法的引入可搭建连接鱼雷壳体结构设计与鱼雷产品可靠性设计之间的理论桥梁。
鱼雷壳体; 安全系数; 可靠度; 二次二阶矩法; ANSYS软件; 概率设计模块
0 引言
目前鱼雷壳体结构强度及稳定性计算还是采用比较保守的安全系数方法, 这种方法虽然可以通过提高安全系数来保证鱼雷壳体结构的安全可靠性, 但是安全系数的选定不可避免地存在人为因素, 选用的不合理会使壳体壁厚及质量过大, 导致内部元件的尺寸与质量受到限制, 降低鱼雷各项战技指标。
在鱼雷行业引入结构可靠性设计理念, 能更加真实地模拟鱼雷变化的工作环境, 并考虑到壳体材料参数变化与加工误差对壳体设计的影响, 使设计出来的鱼雷壳体结构能在满足强度要求的同时, 降低其质量, 从而找到鱼雷安全可靠性能与战技指标间的平衡点。
本文在传统结构设计理念之上, 引入可靠性的设计方法。一方面基于经典壳体强度理论公式确定应用于壳体可靠性计算的安全裕度方程, 并利用二次二阶矩(second order second moment, SOSM) 法、串联系统可靠性计算方法求解壳体结构可靠性指标; 另一方面基于参数化建模方法, 利用ANSYS软件的可靠性设计模块, 从结构有限元角度对壳体结构的强度可靠性进行分析。
1 鱼雷壳体结构组成
鱼雷通常由几个相互独立的舱段组成, 各舱段之间采用楔形环的连接方式。雷体的中部壳体为圆柱段, 头部和尾部壳体为曲线段。鱼雷各舱段的基本结构是用环肋加强的薄壁壳体结构。典型的鱼雷壳体结构由筒体、肋骨、连接环、孔座等主要构件组成, 如图1所示。
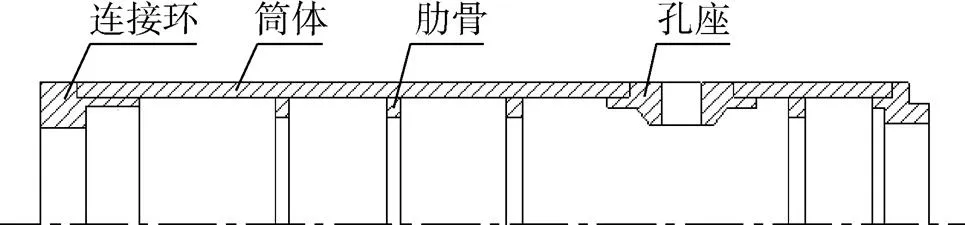
图1 鱼雷壳体组成
2 鱼雷壳体外荷载分析
鱼雷壳体结构外荷载一般包括: 海水压力、管装发射膛压、吊装和运输时的剪力和弯矩、空中吊挂飞行时的激振力、入水冲击力、飞机起降荷载、火箭助推力、开伞过载等。应针对不同工况条件选择不同的设计荷载。
在鱼雷设计时, 一般取壳体工作压力为主要设计荷载, 对其他工况下的特殊荷载进行校核与强度试验, 进一步修改完善设计。壳体工作压力取为鱼雷最大下潜深度或发射深度和膛压之和所确定的最大压力, 用表示, 在进行鱼雷壳体强度设计时, 考虑到计算公式误差、材料性能指标偏差、壳体加工工艺水平以及鱼雷壳体反复使用等因素, 引入安全系数(通常取1.1~1.2), 设计时根据式(1)所确定的计算压力P来进行壳体强度和稳定性校核
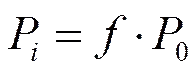
3 鱼雷壳体强度及稳定性校核
鱼雷在均匀静水压力下有2种破坏形式, 其一是由于强度不足, 壳板中的应力超过了材料的屈服极限而破坏; 其二是由于稳定性不足使壳体的局部或总体失稳而失去承载能力。环肋之间的壳板发生屈曲称为局部失稳, 环肋和壳板共同屈曲称为总体失稳。在利用理论公式进行强度及稳定性校核时需对壳体结构形式进行模型化, 在此利用环肋加强的薄壁壳体结构对壳体实际结构进行模型化处理, 如图2所示。

图2 鱼雷壳体结构模型
3.1 强度校核
在进行壳体强度校核时主要针对肋骨跨距中点壳板纵截面上的平均应力、肋骨处壳板横截面上的相当应力及肋骨上的应力进行校核, 具体的校核公式如下。

式中:P为壳体计算压力, MPa;为圆柱壳半径, cm;为壳板厚度, cm;为材料屈服强度, MPa。
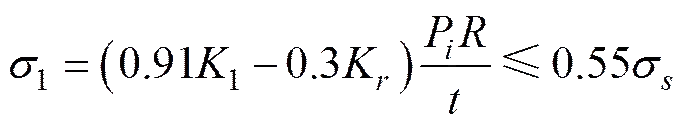
3) 肋骨上的应力及其校核标准为
(4)
3.2 稳定性校核
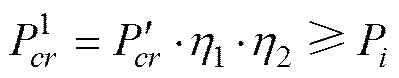
式中:为几何修正系数;为应力修正系数, 可查阅相关手册确定;为局部失稳理论临界压力
(6)
式中:=p/;为失稳波数, 为使最小时的整数值。
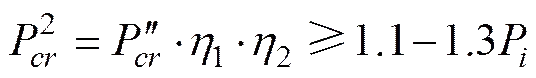
(8)
式中:=p/;为舱段长度, cm;为肋骨连带有效壳板长度联合剖面的截面惯性矩, cm。
4 鱼雷壳体安全裕度方程
4.1 强度安全裕度方程
首先确定基于肋骨跨距中点壳板纵截面上的平均应力的安全裕度方程。
安全方程的一般形式

式中:为结构能力, 针对本研究对象为材料的屈服应力;为荷载效应, 针对本例即肋骨跨距中点壳板纵截面上的平均应力。将式(2)带入并剔除安全系数的影响得到相应安全裕度方程
(10)

其中,,,分别代表肋骨截面的上底、下底与高, 见图3所示(矩形截面肋骨=)。
图3 鱼雷肋骨截面示意图
Fig. 3 Schematic of cross-section of torpedo rib
同理可以确定基于肋骨处壳板横截面上的相当应力的安全裕度方程见式(12), 基于肋骨上应力的安全裕度方程见式(13)。

(13)
由于在强度校核时要求必须同时满足上述3个校核标准, 故在计算基于壳体强度的可靠性指标时可将上述三者按串联结构处理, 并利用串联结构可靠度的计算公式(14)确定壳体强度的可靠度。
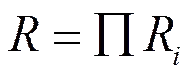
式中:R(=1,2,3)分别表示按照上述强度校核标准确定的可靠性度;为壳体强度可靠度。
4.2 稳定性安全裕度方程
利用上节的方法可以确定局部稳定性及总体稳定性的安全裕度方程分别为式(15)与式(16)。同样也可以按照处理强度可靠度时的方法按照串联结构求解壳体稳定性可靠度。
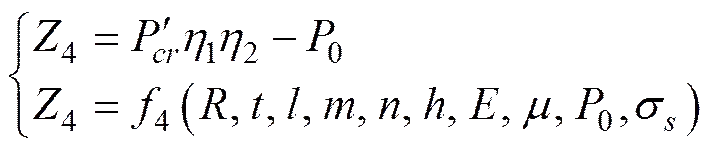
(16)
5 利用SOSM法求解安全裕度方程
由上节分析可以看出, 鱼雷壳体的安全裕度方程体现出很强的非线性, 所以常用的H-L(hasofer- lind)法、改进一次二阶矩(advanced first order second moment, AFOSM) 法并不能满足计算要求, 在此引入求解非线性安全裕度方程计算精度较高的SOSM法。

将随机变量U标准化处理, 有
(18)
将式(18)带入式(17), 得
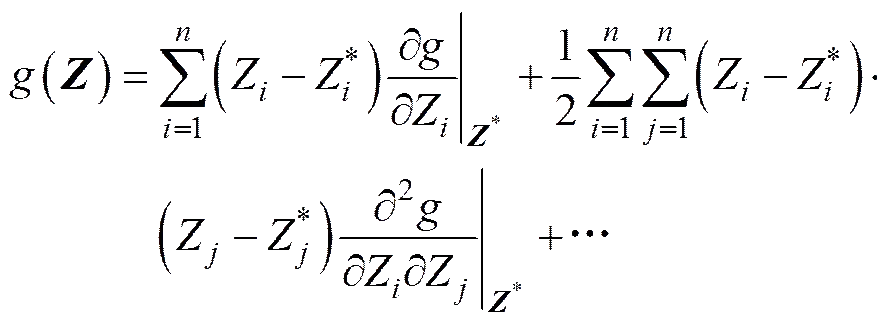
(20)
式中
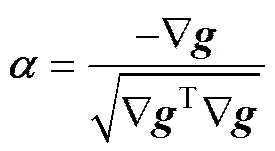
(22)
Ñ=(23)

通过一系列计算可得SOSM可靠性指标为
(25)
式中

其中:b为矩阵的主对角线元素值;为利用AFOSM法确定的一阶可靠性指标。上述计算方法可利用MATLAB软件编制成相应计算软件。
6 结构强度可靠性分析
以上分析均为基于经典鱼雷壳体强度及稳定性经验公式的可靠性分析, 由于经验公式的近似性及模型的简化, 给计算的准确性带来一定影响。在此利用ANSYS软件的概率设计(probabilistic design, PDS)模块结合蒙特卡罗法对鱼雷壳体强度可靠性从有限元角度进行分析。
蒙特卡罗法又称随机抽样法或统计试验法, 是目前结构可靠性计算中一种相对精确的方法。其基本原理: 某事件的概率可以用大量试验中该事件发生的频率来估算, 因此, 可以先对影响可靠性的随机变量进行大量随机抽样, 然后把这些抽样值一组一组地代入功能函数式, 确定结构失效与否, 最后从中求得结构的失效概率。
在ANSYS 的PDS模块中蒙特卡罗法分为直接法、拉丁超立方法和自定义方法3 种,其中拉丁超立方法的效率比直接法高。
在ANSYS中PDS分析技术主要分为以下几个步骤。
1) 生成分析文件
生成分析文件是PDS设计的前提, 对生成的分析文件要求包含完整的分析过程, 具体而言应包括前处理模块、求解模块、后处理模块等内容。PDS正是通过反复调用分析文件来完成可靠性分析的, 因此在分析文件中应尽量剔除不必要的冗余命令。此外在分析文件中必须采用参数化建模方法, 以便于后续的可靠性分析。
2) 可靠性分析阶段
可靠性分析阶段主要包括: 进入可靠性分析模块, 指定可靠性分析文件; 定义输入输出变量分布类型及相应分布参数, 定义输入输出变量之间的相关系数; 选择分析工具和方法; 执行可靠性分析循环, 将结果以文件形式保存等子步骤。
3) 结果后处理
结果后处理过程主要包含绘制结构失效概率分布函数、抽样样本显示、参数灵敏度分析、确定结构的失效概率、自动生成可靠性分析报告等内容。
利用ANSYS软件的PDS模块进行鱼雷壳体结构系统可靠性分析, 理论简单, 计算精度高。但其也存在着一定的缺陷, 最主要的是计算时间的问题。由于蒙特卡罗法的特点, 要想得到精度较高的计算结果就必须采用大量样本进行结构系统的有限元计算, 加之鱼雷壳体结构模型复杂, 一次样本的可靠性计算需花费一定时间, 因此建立在大样本基础上的蒙特卡罗法PDS设计应用受到了一定的限制。此外现今不成熟的鱼雷壳体结构参数化建模技术也给利用PDS进行可靠性分析带来了一定难度。
7 算例
在此结合鱼雷某舱段壳体结构进行可靠性计算分析, 以对比本文所述的2种计算方法。鱼雷某舱段壳体结构形式如图4所示。

图4 鱼雷壳体结构示意图
用于理论可靠性计算简化模型的主要结构参数: 壳体直径28 cm、壳体厚度0.55 cm、舱段长度51 cm、肋骨间距20 cm、肋骨截面(梯形)上底3.5 cm、下底5.5 cm、高1.5 cm。壳体材料弹性模量71 000 MPa、泊松比0.3、屈服强度353 MPa。计算用壳体外压6.6 MPa。为简化计算仅设定主要结构参数为进行可靠性分析的随机变量, 且均服从正态分布形式, 变异系数取为0.03, 各随机变量之间完全独立。
在利用PDS求解鱼雷壳体可靠性过程中, 参数化结构模型中仅取主要结构参数为随机变量且服从正态分布, 各随机变量之间完全独立, 其均值及变异系数可由图纸确定, 蒙特卡罗法样本数取1 000。
按照上文所述2种方法进行结构可靠计算,得到如表1所示计算结果。其中理论计算综合结果为将强度标准与稳定性标准按串联系统处理得出的计算结果。

表1 理论与有限元计算结果对比
通过表1的计算结果可以看出, 理论计算结果与有限元计算结果比较接近, 从而互相验证了2种计算方法的准确性。但是由于理论计算结果用的是简化模型, 不能处理连接环、开孔等壳体局部结构, 故有限元的计算结果更加符合壳体实际结构。为了进一步验证计算的准确性, 还需设计可靠性试验对理论及有限元方法进行比较。
8 结束语
本文以经典鱼雷壳体强度及稳定性校核方法为出发点, 探讨了基于经典理论公式的可靠性求解方法, 编制相应计算程序进行计算, 并利用ANSYS软件的PDS功能建立壳体可靠性求解的有限元方法。上述2种方法的引入为鱼雷结构设计人员与可靠性工程人员提供了一种新的设计思路与方法。
[1] 徐宣志, 欧阳吕伟. 鱼雷力学[M]. 北京: 国防工业出版社, 1992.
[2] 龚庆祥. 型号可靠性工程手册[M]. 北京: 国防工业出版社, 2007.
[3] Cornell C A. Structural Safety Specification Based on Second-moment Reliability[J]. Symposium International Association of Bridge and Structural Engineering, 1969, 7(2): 5-9.
[4] 王呼佳, 陈洪军. ANSYS工程分析进阶实例[M]. 北京:中国水利水电出版社, 2006.
[5] 徐钟济. 蒙特卡罗法[M]. 上海: 上海科学技术出版社, 1985.
(责任编辑: 陈 曦)
Reliability Analysis of Torpedo Shell Based on Strength and Stability
GUO Jun, JIANG Zhong-liang, QIN Xiao-hui, LIU Jin
(1. The 705th Research Institute, China Shipbuilding Industry Corporation, Xi′an 710075, China; 2. Xi′an Modern Chemistry Research Institute, Xi′an 710065, China)
The concept of reliability design is introduced into torpedo structure design to rectify the insufficiencies of the conventional safety coefficient method. A safety margin equation and the solving approach of torpedo shell structural reliability based on a theoretical formula are proposed by combining the classic theory of torpedo shell and the second-order second-moment method. Simulation of torpedo shell structure by using the probabilistic design system(PDS) module in software ANSYS is performed to achieve its reliability. The proposed scheme combines structure design with reliability design, which may facilitate the design of torpedo shell.
torpedo shell; safety coefficient; reliability; second-order second-moment method; ANSYS software; probabilistic design system(PDS) module
TJ630.3
A
1673-1948(2011)06-0401-05
2011-05-19;
2011-06-27.
郭 君(1980-), 男, 博士, 工程师, 长期从事结构系统可靠性设计与计算方面的研究.

