用于微小卫星自主导航控制系统地面仿真的磁强计数学模型

党朝辉,项军华,刘 昆

(国防科学技术大学 航天与材料工程学院,湖南 长沙 410073)

0 引言

对应急卫星、战术卫星等微小卫星来说,采用磁强计定姿和定轨的自主导航方法具有质量轻、功耗小、可靠性高和成本低等特点[1]。目前,用于微小卫星自主导航控制系统的磁强计数学模型尚未被系统建立。在有关磁强计自主导航的文献中,通常都未明确给出仿真系统中磁强计测量数据获取的具体实现方法。文献[1]介绍了一种地磁动态模拟器的构建方法,说明了地磁场数据生成的方法及地磁模拟器输出电流与其对应的关系,但没有给出磁强计测量数据生成的方法。文献[2、3]采用在地磁场理论计算值的基础上添加测量噪声的方法,这种测量噪声通常是符合高斯分布的零均值随机噪声,但真实的磁强计除测量噪声外,还包括系统误差,具体可分为偏移误差、非正交误差和尺度因子误差3类[4]。此3类误差需分别建立精确的数学模型,并结合地面仿真系统的特点进行相关处理。本文对某卫星控制系统地面仿真用磁强计数学模型的建立进行了研究。

1 磁强计数学模型

基于磁强计自主导航控制系统的地面仿真原理如图1所示。图中：F,M分别为控制力和力矩;ΔF,ΔM分别为干扰力和干扰力矩;θ为卫星在参考坐标系中的姿态角矢量;r为卫星在惯性坐标系中的位置矢量;ε为测量噪声;B为磁场强度。在该仿真系统中,磁强计的数学模型用于模仿磁强计在真实环境中的工作状况,其输入为轨道动力学和姿态动力学积分结果,输出为磁强计测得的地磁场强度矢量。卫星姿态、轨道确定模块利用该地磁场强度矢量确定姿态和轨道,其结果作为控制器的输入。控制器的推力器和磁力力矩器分别产生控制力与力矩,作为卫星轨道和姿态动力学模块的输入。整个过程形成一完整的闭环。

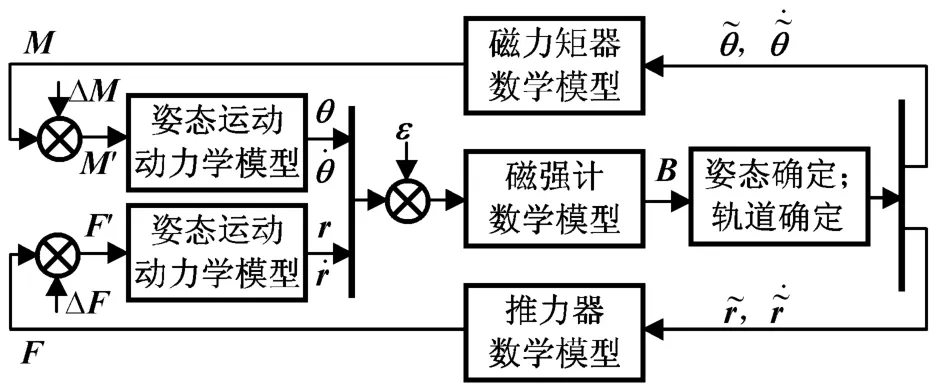
图1 磁强计自主导航控制系统地面仿真原理Fig.1 Principle of ground simulation system for automatic navigation based on magnetometer

1.1 磁强计工作原理

磁强计内部装有铁心,当铁心处于过饱和状态时,其磁导率随激磁磁场强度而变,感应电动势中就会出现随环境磁场而变的偶次谐波增量;当铁心处于周期性过饱和工作状态时,偶次谐波增量将显著增大,磁强计即利用此磁通门物理现象测量环境磁场[5]。安装在卫星上的三轴磁强计(TAM)在卫星轨道上工作时,磁通门探头感应到地球磁场后,相应的磁通量被调制成偶次谐波感应电势,该电势在3个敏感轴上的分量就代表了当地地磁场矢量在3个敏感轴上的分量。

1.2 地磁场生成模型

在卫星控制系统的地面仿真系统中,对磁强计建模仿真时,首先需构造地磁环境,这便需使用地磁场模型。地磁场是围绕地球周围自然发生的一种微弱磁场,历史上先后建立了多种地磁场模型,其中以高斯球谐函数的表达式最著名[6]。由国际地磁场和高层大气物理协会(IAGA)建立的国际地磁场参考模型(IGRF)被广为使用,该参考模型是通过天文观测、船舶、飞机、卫星,以及地面测量等获得的地磁场实测数据而建立的,迄今为止,已有多种IGRF(1900～2015)模型可供使用。由于地磁场随时间不断变化,IGRF的地磁场模型每5年更新1次。本文采用了最新的地磁场模型及其参数,即IGRF2010模型。

地磁场强度矢量Bm为势场,在地球中心球坐标系中可写作标量势的负梯度[4]。即

式中：V为势函数,其高斯球谐系数形式展开为

此处：Re为地球参考半径;N为球谐展开的最大次数;为与时间相关的m阶n次高斯系数;λ,φ′,r,t分别为在地球中心球坐标系中的经度、纬度、地心距和时间;为施密特函数,且为半标准化的连带勒让德多项式,定义为

地磁场常用北东地坐标系,如图2所示。

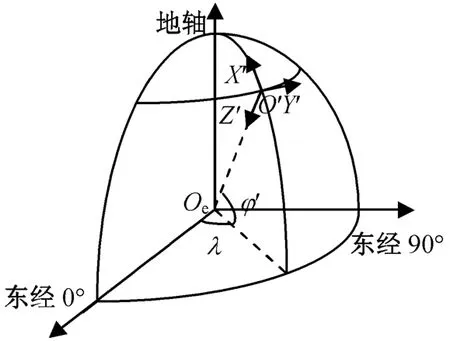
图2 北东地坐标系Fig.2 North-east-down coordinates

式(2)在北东地三个方向求负梯度,可得地磁场强度表达式为

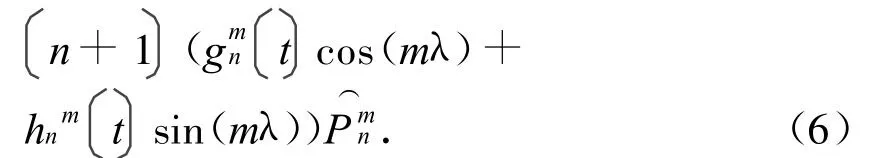
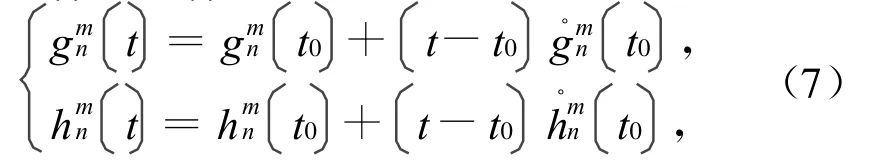
且t按小数形式表示[4]。此处：t0=2010.0表示IGRF2010模型的参考基准时刻,t的有效范围是2010年1月1日至2014年12月31日,超出此时间段就要采用其他模型。模型中,为主磁场系数;为长期变动系数,这些参数的具体取值可在IGRF2010的参数表中获取。IGRF2010的高斯系数取至12阶,其中前3项高斯系数值见表1,其余参数取值详见文献[4]。

表1 IGRF2010国际地磁场系数Tab.1 Gauss coefficients of IGRF2010

1.3 磁强计测量模型

磁强计安装在卫星上,随卫星运动获取卫星轨道上的地磁场强度,理论上磁强计的测量数据即为其所处位置地磁场的真实值。因此,理想状况下磁强计的测量数据可通过本文建立的地磁场生成模型求取。但真实的磁强计由于制造、安装和本身磁性元件存在各种误差,其实际测量值会与地磁场模型理论值存在差异。磁强计的各种误差可分为偏移误差、非正交误差、尺度因子误差和测量噪声4类。

a)偏移误差

是由实际磁强计电路温漂、磁心剩磁等引起的误差,表现为即使环境磁场为0时仍有微小输出。设该输出为,则磁强计实际测量值b1、理论测量值b与偏移误差b0满足关系

b)非正交误差

是指实际磁强计的三轴未互相正交产生的测量误差。实际磁强计非正交三轴与理想正交三轴的转换关系如图3所示[7]。图中：O-X1Y1Z1,O-X2Y2Z2分别为理想正交和实际非正交三轴构成的坐标系;为便于分析,设OZ1、OZ2轴重合;OY2轴在平面Y1OZ1内;OX2轴与平面X1OY1夹角为α0;OX1轴与平面X2OZ2夹角为γ0,且OY2、OY1轴夹角为β0。

图3 磁强计实际与理想正交三轴坐标系的转换关系Fig.3 Relationship between true and ideal magnetometer coordinate system

由图3的几何关系,将O-X1Y1Z1系中的磁场强度矢量转换至O-X2Y2Z2系中,可得实际磁场强度测量值b2与b1满足关系

c)尺度因子误差

是由磁强计3个敏感轴的制造误差产生的。该误差表现为同样大小的磁强由各轴单独测量时有微小差异[8]。设三轴的尺度因子误差分别为kx,ky,kz,则磁强计实际测量值b3与b2满足关系

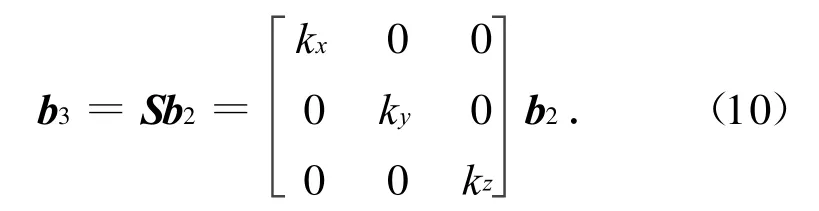
d)测量噪声

磁强计的测量值中还含有测量噪声ε,一般为零均值的高斯白噪声,方差Σ=E[εεT]。

综合上述误差,可得在磁强计体坐标系中磁强计测量值

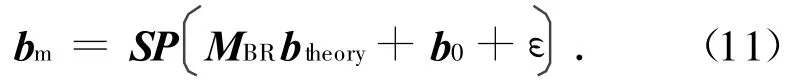
式中：bm为磁强计体坐标系中的磁强计真实输出;S为尺度因子误差阵;P为非正交误差阵;MBR为磁强计体系(B系)相对参考系(R系,北东地)的姿态矩阵;btheroy为由地磁模型所得的R系中的理论磁场强度;b0为B系中的偏移误差;ε为地磁观测噪声。

为与理论计算比较,设bmeasure为R系中的磁强计测量值bm,有

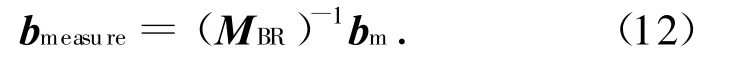
则bmeasure,btheory间的差异反映了真实磁强计测量值与地磁场模型理论计算值的差异。

1.4 磁强计测量数据生成算法

根据上述地磁场生成模型和磁强计测量模型,在微小卫星地面仿真控制系统中,磁强计测量数据的生成可以分为3步：一通过卫星轨道动力学和姿态动力学模型获取卫星实时位置和姿态;二将卫星位置转换为地理经纬度值,代入式(4)～(6),计算地磁场强度的理论值;三将地磁场强度理论值代入式(11),获得磁强计的测量数据。其中,S,P,b0所对应的9个误差模型参数α0,β0,γ0,kx,ky,kz,b0x,b0y,b0z为已知。

2 仿真

设仿真条件为：取地球圆形轨道高度300 km,磁强计安装体轴与卫星体轴保持一致;地磁场生成模型中的高斯系数取自IGRF2010模型,具体数值详见文献[4];磁强计误差参数取值见表2;ε为高斯白噪声,其在3个体轴方向的均方差均为10 nT。所得仿真结果如图4、5所示。图5中：理论误差是由地磁场生成模型算得的磁场强度(btheroy)与真实磁强计在轨实测数据(bmeasure)间的差值;生成误差是由本文磁强计测量数据生成模型算得的磁场强度(bgenerate)与bmeasure间的差值,其中磁强计在轨实测数据来自参考文献[9]。该图中的地磁场强度的具体数值见表3。

图4 轨道高度300 km处磁强计生成值Fig.4 Generating measure data of magnetometer on orbit with height 300 km

图5 地磁场强度理论误差及生成误差Fig.5 Theoretical error and generating error of magnetic field data

由图4可知：该图形状与全球地磁场理论模型基本一致,表明本文建立的磁强计数学模型得到的测量数据具有可信度。由图5可知：理论误差远大于生成误差,用地磁场理论值作为地面系统中磁强计的测量值不可信,而生成误差在R系的三个方向(对应x、y、z轴)的误差基本小于100 nT,说明该模型较好地模拟了磁强计的工作特性。

3 结论

本文建立了用于微小卫星自主导航控制系统地面仿真用的磁强计数学模型,给出了构造磁强计测量数据的算法。仿真表明,本文建立的磁强计数学模型能较好地模拟真实磁强计的工作特性,所得磁强计测量数据与真实测量数据符合一致,可作为微小卫星自主导航控制系统地面仿真所用的磁强计数学模型。

表2 误差参数列表Tab.2 List of error parameter

表3 300 km高度地磁场理论计算值、磁强计在轨实测值、按照本文算法得到的磁强计生成值Tab.3 Theoretical value,measurevalue and generating valueof magnetic field on 300 km orbit

[1]袁胜华,易 忠,马慧媛.中低轨道地磁动态模拟器[J].航天器环境工程,2006,23(3)：146-150.

[2]荣思远,崔乃刚.一种基于磁强计的卫星自主导航方法研究[J].上海航天,2006,23(3)：16-18.

[3]张 锐,朱振才,张 静,等.基于磁强计的微小卫星姿态确定[J].宇航学报,2006,27(4)：578-579.

[4]MAUS S,MACMILLAN S,MCLEAN S,et al.The US/UK world magnetic model for 2010-2015[EB/MO].[2009-11-03].http：//www.ngdc.noaa.gov/geomag/WMM.

[5]曹红松,陈国光,赵捍东,等.姿态测试用磁通门磁强计的设计[J].弹道学报,2002,14(5)：79-80.

[6]JURSA AS.Handbook of geophysics and the space environment[R].Air Force Laboratory,Air Force Systems Command USAF,NTIS Document ADA 167000,1985.

[7]林春生,向 前,龚沈光.三轴磁强计正交误差分析与校正[J].探测与控制学报,2006,27(2)：9-12.

[8]ALONSO R,SHUSTER M D.Complete linear attitude-independent magnetometer calibration[J].Journal of Guidance,Control and Dynamics.2005,28(1)：115-120.

[9]王宇飞.基于地磁环境仿真系统的卫星导航算法研究[D].哈尔滨：哈尔滨工业大学,2006.